来源：https://blog.csdn.net/baidu_39413110/article/details/103466261

好的模型变量直接决定着一个风险模型是否稳定和有效，而好的模型变量都具备以下三种特性：
1、变量自身的分布是随时间相对稳定的；
2、变量和目标值之间是有强相关关系的；
3、变量和目标值的强相关关系也是随时间相对稳定的；

建模初期所有的变量筛选工作都是围绕着这三点来寻找符合这些特性的变量的。

一变量自身分布稳定性

psi
风控中常用的衡量稳定性的指标是psi：

psi = sum((实际占比-预期占比) * ln(实际占比/预期占比))

建模初期，对变量稳定性进行筛选的一个常用方法为：选择第一天（或最后一天）做为基准日，将后续每日的数据都同基准日的数据计算psi，一旦有一天或几天的psi值超过一个阈值（一般为0.1），则删除该变量，当然也可以将时间尺度扩大到周或者月。这是一个高效的方法，但也存在以下几点问题：

1、计算psi需要单独处理缺失值。这个问题当然可以解决，解决办法就是将所有的缺失值单独分为一组，但当一个变量缺失率过高的时候，会导致非缺失的其它分组占比过少，就会带来第二个问题；

2、计算psi要注意某一组占比变为0的情况。假设我们将基准日的变量分了5组，因为变量本身分布的波动，在以同样的切分点对第二日的变量进行分组时，有时会发现某一组的占比竟然为0，而ln(0)是无法计算的，就会导致psi的计算报错。这种情况在某一分组占比较少时很容易发生，如图中所示，基准日的数据分了5组，而因为变量分布波动，第一日的数据中分组3的占比就变成了0。当然这个问题也可以这样解决，当某一组出现了0占比的情况时，那在计算psi的时候就将这一组去掉，只用剩下的组计算就好了，这样做不失为一种方法，但有时会掩盖一些问题，我们在下面的例子中会分析这个一点；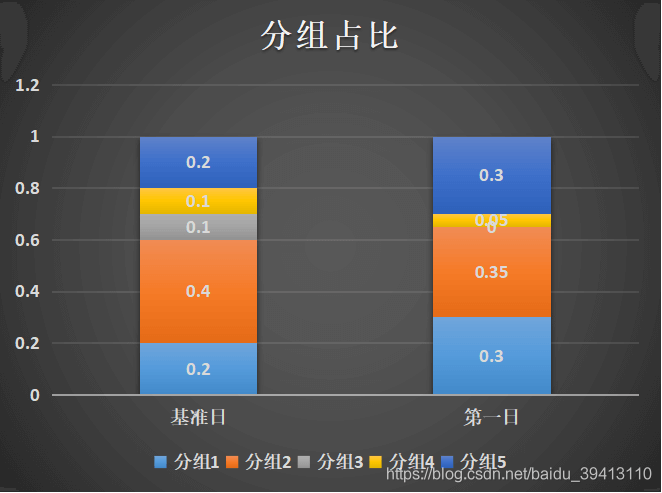

3、psi只能告诉我们变量分布变动是否较大，不能告诉我们变量具体是往哪个方向偏移的，以及每一个分组占比的具体变化情况。

长期趋势图
所以，相比于前期简单粗暴地定一个psi阈值进行变量剔除，我们更推荐后期查看每一个变量的长期趋势分布图，这会帮助我们发现更多变量的问题。来看一个案例：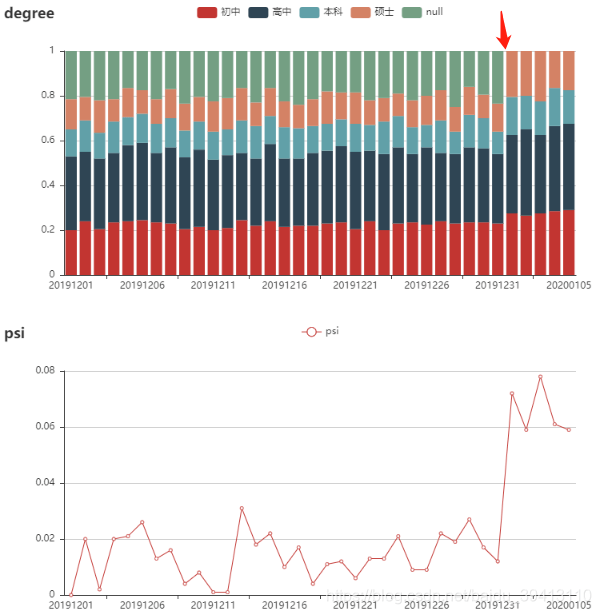

图中虚构了一个学历变量的长期趋势分布，可以看到学历这个变量每天的分布都没有太大的波动，如果它对预测y长期有效的话，那它将会是一个很好的变量；但是，从2020年1月1日开始，学历这个变量的缺失值那一组消失了，假如说学历这个变量对y的区分度主要来自于缺失和非缺失（现实中往往如此，缺失很可能代表客户不想过多透露信息，而这样的人通常坏的概率更高），那从这个时间点开始，学历这个变量对y的预测能力将有很大衰减，从而导致模型效果的衰退；这种缺失可能是产品的改动导致的，也可能是策略的调整引起的，但如果后续不能将学历变量的分布恢复如初，那训练模型的时候就不能将其放到备选变量库中。

现在来说另一个问题，这种波动能不能通过psi这个指标发现呢？为此，我们把第一天做为基准日，后续每天同第一天的数据计算了psi，如上所述，当某一组出现0占比的时候，我们就把这一组踢掉再计算psi（图2下）。可以看到，虽然从2020年1月1日起，psi明显升高了，从0.02左右跳升到0.08上下，但如果我们只以0.1作为阈值，那学历这个变量是完全满足稳定性条件的(并不能发现如果用psi)，如果不做详细分析，那缺失组消失的问题也就被忽视了。

最后提一点，这种长期趋势一般看的是整个进件人群，这样反映的才是变量本身有没有在波动；与之相对应的，如果我们看的是通过件人群的变量长期分布，那这个分布很大程度上受通过率的影响，换言之，通过策略每一次变动都很有可能导致变量分布产生一次大的波动，而这并不是变量本身的问题。

附：图2造数据和使用pyecharts绘图的python代码：

#requirements: pandas==0.2.3 numpy==1.16.4 pyecharts==0.5.11
import pandas as pd
import numpy as np
from pyecharts import Bar,Line,Page
##造数据
column = list(map(str,range(20191201,20191232)))
column = column+list(map(str,range(20200101,20200106)))
df = pd.DataFrame()
df['初中'] = [0.2+np.random.randint(0,10)*0.005 for i in range(31)]
df['高中'] = [0.3+np.random.randint(0,10)*0.005 for i in range(31)]
df['本科'] = [0.1+np.random.randint(0,10)*0.005 for i in range(31)]
df['硕士'] = [0.1+np.random.randint(0,10)*0.005 for i in range(31)]
df['null'] = 1-df['初中']-df['高中']-df['本科']-df['硕士']
df2 = pd.DataFrame()
df2['初中'] = [0.25+np.random.randint(0,10)*0.005 for i in range(5)]
df2['高中'] = [0.35+np.random.randint(0,10)*0.005 for i in range(5)]
df2['本科'] = [0.15+np.random.randint(0,10)*0.005 for i in range(5)]
df2['硕士'] = 1-df2['初中']-df2['高中']-df2['本科']
df2['null'] = 0
df = pd.concat([df,df2],ignore_index=True)
print(len(column))
print(df.shape)
##将分布以柱状图的形式画出
bar = Bar('degree')
for i,item in enumerate(df.columns):
    bar.add(item,column,df.iloc[:,i],is_stack=True)
##psi计算
psi = []
for i,item in df.iterrows():
    if 0 in item.values:
        this_day = item.values[:-1]
        base_day = df.iloc[0,:-1].values
    else:
        this_day = item.values
        base_day = df.iloc[0,:].values
    dif = base_day-this_day
    ln = list(map(np.log,base_day/this_day))
    this_psi = sum([x*y for x,y in zip(dif,ln)])
    psi.append(round(this_psi,3))
##将psi以折现图的形式画出
line = Line('psi')
line.add('psi',column,psi)
##把柱状图和折现图放到一个page里
page = Page()
page.add(bar)
page.add(line)
page.render('degree&psi.html')

二变量和目标值的强相关关系

IV值

变量和目标值之间有强相关关系指的是变量能够有效区分出好人和坏人；仍以学历这个变量为例，如果我们发现学历越高的人群坏人占比越低，也就是说在处在不同学历区间的人群有着明显的坏账率差异，那么学历就是一个和目标值有强相关关系的变量，且这种坏账差异越大，相关关系就越强，对好坏人群的区分度就越高。那有没有一个指标可以量化这种区分度呢？就是风控中常用的IV值（Information Value）：

IV = sum( (该组坏人占比-该组好人占比)ln(该组坏人占比/该组好人占比) ) = sum( (该组坏人占比-该组好人占比)该组WOE )

从IV值的计算公式中可以看到IV值的两点优势：

1、IV值一定不会是负数（因为(该组坏人占比-该组好人占比)和该组的WOE值一定是同号的），越大表示变量的区分度越好，很符合我们对一个量化指标的预期；

2、IV值同时兼顾了每组样本的数量和对目标的区分能力，使得IV能够避免小样本分组的干扰，更好地衡量变量的整体预测性，举个例子：

假设学历变量分布如上表，可以看到“初中”这个分组对坏人的区分度非常高，坏账率达到了80%，所以这一组的WOE值也比其他组的WOE高出了一个量级；但很遗憾，这一组的人数实在太少了，只占总人数的5‰，所以即便这组有如此高的区分度，但对整个样本区分度的贡献还是非常有限。在计算IV值的时候，(该组坏人占比-该组好人占比)这一项就涵盖了样本量的信息，样本量越小，这一项的值就会越小，所以“初中”这一组的单组IV值计算出来也和其它组差不多，最终的IV值也不会因为样本量极少的这一组的高区分度而变得虚高。

IV值是衡量变量区分度的一个相当有效的指标，但IV值也有其不足，就是衡量不了变量间的相互作用；那什么方式可以将变量间的相互作用也涵盖进去呢，可以用模型重要性排序的方式，比如常用的随机森林或者XGBoost的变量重要性排序。

变量数的选择

在建模过程中，我们一般用IV值对变量进行初期的筛选，根据需求，可将IV值阈值卡在0.01左右，再小的话，即便把这样的变量放进来，对模型的整体提升也不会有太大增益。对IV值筛选后的变量，我们再放到XGBoost中进行排序（推荐将XGB的重要性排序标准的参数调成gain），根据重要性从高到低，选择一定数目的变量进行建模。

那为什么要选择一定数目的变量，而不是都拿来建模呢？主要是基于两方面考虑：

一是变量越多越容易过拟合，训练速度也会变慢；

二是变量开发上线以及后期监控维护都是需要成本的，当不带来更多增益的情况下，完全没有必要使用更多变量。（实际业务中会发现，往往前几个变量已经主导了最终的模型效果，尤其是有综合性分数类变量在的时候）

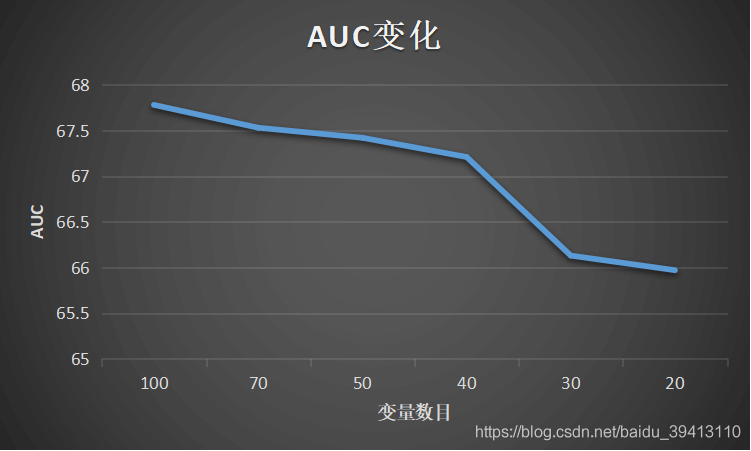
那到底最终应该选择多少变量呢？可以采用如下方式：分布尝试100, 70, 50 … 20个变量入模，看一下AUC衰减情况，下图这个例子中，变量数从100减少到40，模型的整体AUC也只下降了0.5个点左右，但如果再继续减少，AUC就有了明显衰减，所以40个左右的变量是在保证一定模型效果的情况下，开发和维护成本最小的方案，在资源有限的情况下，这也是最优方案。

三变量和目标值相关关系的稳定性

各个数据集上趋势一致

一般建模都会拆分三个数据集：train、test和oot；train上做训练，test上测试，oot用来验证模型在时间外样本上的稳定性。三个数据集不仅可以用于模型，同样也可以用来检验和筛选变量。
好的变量在各个数据集上和目标值关系的趋势都是一致的，为了方便检验每个变量在各数据集上的趋势，我们一般会查看每个变量的分箱坏账图，以虚构的年龄变量为例，图中能明显看出随着年龄的增加，坏账率在三个数据集上都是随之升高的（线图），但在最后一个分箱上坏账看起来很不一致，但关注一下这个分箱的人数占比（柱状图）可以发现，这个分箱只有2%左右的人，在样本不足够大时，有波动也很正常，所以，一般我们会把分箱占比和坏账放在一起分析查看。当然，将人数占比放进来也有另一个好处，就是方便我们看到变量在不同数据集上的分布是否稳定。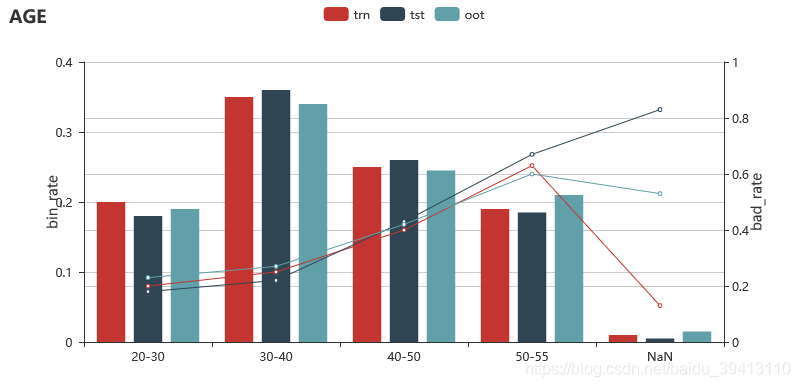

在各个数据集上看变量的分箱坏账图能够一定程度上检验变量与目标关系的稳定性，但如果需要更细化时段，或在更长的时间段（比如最新的数据，比如oot2，oot3）上去检验，我们还可以看另外两种图。

变量预测效果不衰减

上一节我们提到IV值是检验变量预测效果的一个很不错的指标，那为了检验变量预测效果不随时间衰减，我们可以把数据集按时间分成若干时段，每个时段计算IV值，形成IV时间趋势图。一般意义上，预测能力稳定的变量iv值是不会随时间有明显衰减的，所以iv趋势图可以帮助我们检验变量是不是已经失效了。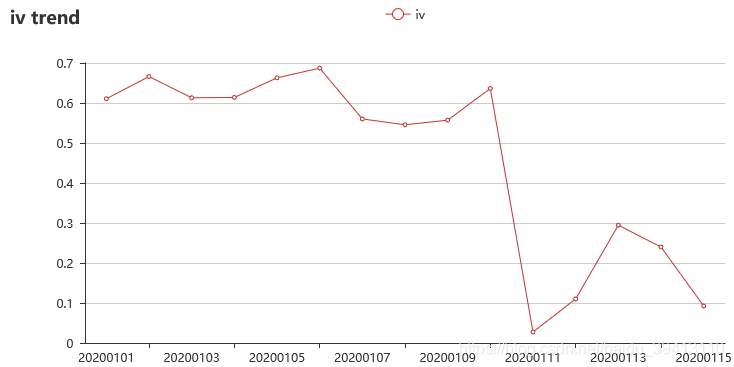

如上图所示，该变量的iv值在2020年1月11日发生了明显的下降，那建模的时候这个变量是不是就不能用了？不可以轻易下结论。风控建模一定是和业务紧密联系的，这时我们应该去查清楚，在1月11日这个时点是不是启用了一个相关变量的策略字段，或者上线了一个含有该变量的模型，导致了这个时点之后的表现人群都是经过这个变量筛选过的，才使得这个变量的iv降低。

假如线上有一个模型A在决策，模型是包含该变量的，如果我们本次迭代模型B是为了替换线上的A模型，那这个变量一定是要用上的，但如果模型A将继续用于决策，本次模型B只为增补它用，那这个变量应该考虑去掉，不然1月11日之前的模型效果只会虚高。

变量预测方式不反转

当我们检验了变量的IV趋势并发现它是基本平稳的，是不是就说明这个变量的预测能力是没有问题的呢？还不够，在检验IV趋势图时，我们往往还需要配合另一张图一起看，就是分箱坏账趋势图。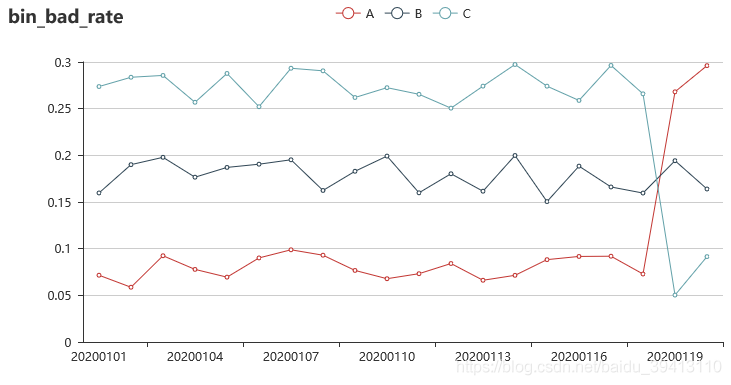

假设一个变量分了三箱，我们把每箱的坏账率随时间的变化画在一张图上就是上图展示的分箱坏账图，如果单单考察这个变量的IV趋势，会发现IV随时间是相当稳定的，区分力一直都在，但上面的分箱坏账趋势图就能告诉我们，虽然区分力在，但区分方式已经变了，本来A箱一直都是最优质人群，C箱最坏，但在1月19日之后，A和C两箱的坏账率颠倒了，最好成了最坏；这就会直接导致模型的区分效果下降。所以面对这种变量，建模基本也是不能使用的。
————————————————
版权声明：本文为CSDN博主「白白的一团团」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/baidu_39413110/article/details/103466261

YT库

风控建模三：变量筛选原则

一变量自身分布稳定性

二变量和目标值的强相关关系