SVM

来源：
https://blog.csdn.net/sinat_32849897/article/details/120030622
https://zhuanlan.zhihu.com/p/77450726

支持向量机（Support Vector Machine，SVM）模型是一款性能表现出色、知名度很高的机器学习模型，常用于解决分类问题。但支持向量机涉及较复杂的数学公式推导，容易让初学者让而却步，不敢深究其内在原理。其实，支持向量机和最简单的分类模型——Logistics回归模型——的基本原理都是一样，都是想用线性方法解决分类问题。
但是，线性方法存在明显的局限性，那就是无法解决非线性的分类问题，这个局限也就成为线性分类器的性能天花板。而支持向量机之所以成功，就是使用一系列的数学方法，就像一套配合完美的组合拳，巧妙突破了这个天花板限制。
这套组合拳大概可以分为三个部分：最大间隔、高维映射和核方法，其中高维映射是支持向量机可以用线性方法解决非线性分类问题的关键，弄明白了这个，就弄明白了支持向量机最核心的数学原理。

1. 从更高维度看“线性不可分”

用线性方法分类就是用一条“直线”——当然有时候可能是多维的“直线”也就是平面——来划分数据。这种方法实际是在正类和负类之间找到一个能插入直线的间隔，但遇到数据非线性分布，也就是真正意义上的“间不容发”的情况，这套线性分类方法就失灵了。
在很多情况下，不同类别的数据分布并不像象棋那样泾渭分明，只需要简单地找出一条分界线，而是混杂在一起，我中有你你中有我，更为形象地说，大部分的数据不像是象棋，而更像是杀得犬牙交错的围棋，无法用线性加以区分，术语很形象地称为线性不可分。
可是，线性不可分真的就是线性分类器的尽头了吗？
支持向量机创造性地引入高维映射巧妙解决了这个问题。高维映射是支持向量机最让人尖叫的部分，也是数学在机器学习算法里能够达到的巅峰。数学有一种思路，遇到新的难题，通常解决分两步。第一步，将新问题转化成已经解决的就问题；第二步，完成转化后，通过老方法加以解决。我们要解决的问题就是，怎样为线性不可分变得线性可分，然后再按老办法寻找最大间隔。
让线性不可分线性可分，这不是矛盾吗？不矛盾。线性不可分，只是在当前的维度下线性不可分，但如果增加了维度，原本不可分也就可分了。还是以刚才的围棋为例，围棋顾名思义，棋子都是黑子白字互相包围在一起的，属于线性不可分。但假设有一个武林高手暗运掌力，忽然快速往棋盘上一排，让白子黑子都垂直往上飞起，同时让黑子飞高一点，白子则相对低一些，这样，平面无法线性区分的黑白子门，在进入立体空间，多了高度这个维度之后，就体现出了区别。这时，只要往飞升的黑白子之间塞入一张薄纸，就把两种棋子分开了。二维的叫线，三维的叫面，超过三维的不另外改名字了，统一都叫超平面。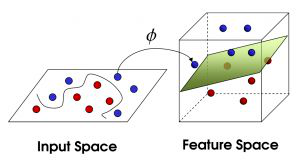

2. 高维映射

大多数介绍支持向量机的教材，说到这里也就差不多了，但这容易引来了两个让人困扰的问题：一个理论层面的质疑：为什么映射到高维就能保证正负类能够上下分开这么凑巧？一个是应用层面的问题：这个高维空间要怎么找？变成高维空间容易，增加一个维度就能达到提升空间维度，一直增加下去也就成了高维空间，可是肯定不是简单地增加维度就能分开，还得给原有数据点在新的空间里安排位置对吧，那怎么知道怎么安排才合适？
为了说清楚这个问题，首先还是让我们回到最初的地方：我们要解决什么问题？线性不可分问题，具体来说，就是正类和负类混杂在一起，你中有我我中有你，无法简单地插入一根线进行区分。
这就好办了。我们把问题形象化，为这个“你中有我我中有你”想象一个具体的样子，不如就想象一根铁丝，上面串了三枚五角星，我们的目标是用一根直线，分出中间的五角星。
显然这是个线性不可分问题。无论直线怎么摆放，中间的五角星一定都会至少和一枚侧边的五角星在一边，无法正确区分。不过，这个看似不可能的任务，只要稍微弯一下铁丝，铁丝形成一个U型。这时，中间的五角星处在了低端，而两边的五角星被抬高了，这时只要横着往中间插一根直线，就能正确区分二者。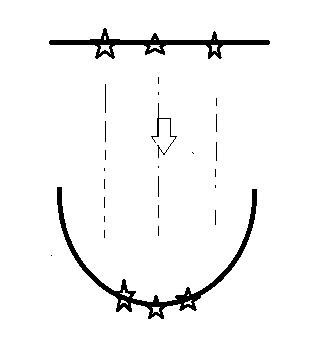

3. 真实世界的高维映射

也许一个点看着不够味，那我们来看看更贴近我们熟悉的数据集样本情况。再次明确一下，我们现在正在处理的是如何用线性方法处理线性不可分数据的问题，那么首先就是数据分布的情况。
既然是线性不可分，那可以推想需要区别的两类数据点处于一种你中有我或者我中有你的状态，最极端的就是一类数据被另一类“包围”，如果用红色和绿色区别这两类数据，图像就变成了“万绿丛中一点红”，在这种情况下显然不可能用任何一条直线划分二者，也就是无法使用线性方法进行分类（如下图左）。
现在我们进行高维映射。这里我们选择肉眼可见的方法，就把高维映射想象成在二维空间中倒扣上一只肚子朝上的漏斗，二维空间就变成了三维空间，我们把漏斗移动到红色类的数据上方，这时两种颜色的数据就出现了高度差，这时就可以通过插入一块平板分隔二者，也就是可以采用线性的方式进行非线性数据的区分了区分（如下图右）：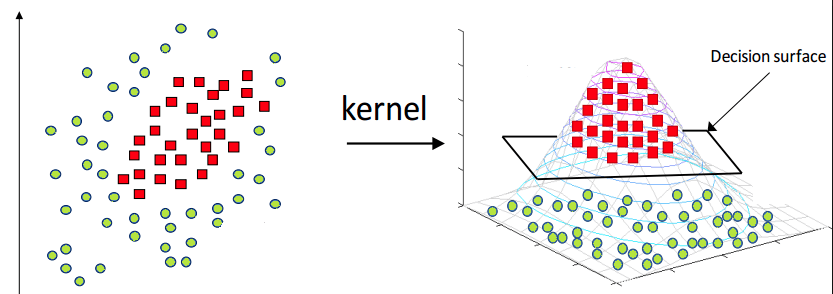

总结一下，非线性数据之所以可以用线性方法区别区分，是因为给原本只有“左右”区别的五角星，增加了“上下”的维度，出现了线性可分的差别。从另一个角度看，这也是一种用映射方法来解决问题的案例。直线有直线方程，弧线有弧线方程，只需要通过一个映射，就能使得原本线性排列的数据呈弧线排列。对于机器学习用映射来解决问题我们并不陌生，回忆一下，Logistics回归里的S型函数就是这种手法。这就是增加维度来解决线性不可分的问题关键，知道当前分布是什么样子，知道想要达到的分布是什么样子，那么，只要选择合适的映射函数，也就解决了第二个问题。

支持向量机的优缺点

每个分类算法都有自己的优点和缺点，它们根据正在分析的数据集发挥作用。

SVM的一些优点如下：

• 凸优化方法的本质是保证最优性。该解决方案保证是全局最小值，而不是局部最小值
• SVM是一种适用于线性和非线性可分离数据（使用核函数技巧）的算法。唯一要做的是找出正则化项C
• SVM在低维和高维数据空间上工作良好。它能有效地对高维数据集工作，因为SVM中的训练数据集的复杂度通常由支持向量的数量而不是维度来表征。即使删除所有其他训练示例并重复训练，我们将获得相同的最佳分离超平面。

• SVM可以在较小的训练数据集上工作，因为它们不依赖于整个数据。

  SVM的缺点如下：

• 它们不适合较大的数据集，因为在较大的数据集上使用SVM的训练时间可能很高，并且计算量更大。

• 它们在具有重叠类的嘈杂数据集上效率较低。