万物皆网络，万字长文详解社区发现算法Louvain：https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650192424&idx=1&sn=df51fdc3f4c515eb094f0a476bf55ea9&chksm=88239decbf5414fabfb0198f627e714f2a93c497c317be9b39014051245806d5f945d1dbf697&scene=21#wechat_redirect

风控必读：Louvain、LPA等5类经典社区发现算法的实现策略与开源实现：https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650190951&idx=2&sn=4ef85069b850fdf985246b2b6acbe3a6&chksm=882393a3bf541ab565410ca71ce7650cdfe485394a9286c95ababdd73a36ee1239523b28d87f&scene=21#wechat_redirect

社区发现之标签传播算法（LPA）：https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650190420&idx=1&sn=16eb3b1e30e797b7725fc571f5645d16&chksm=88239590bf541c86590bec30f298616ecac754d514b613235cc11727b22d2b983a3f660fa4fe&scene=21#wechat_redirect

【1】风控必读：Louvain、LPA等5类经典社区发现算法的实现策略与开源实现

本文我们将继续沿着社区发现这个主题，对现有的几个经典社区发现算法，从实现思想，实现代码以及效果展示几个方面进行介绍。
在本文中，主要参了CSDN博主「东方小虾米」的一些算法总结，很有参考意义，对此表示感谢，在此基础上，利用开源工具networkx进行实践，大家可以看到具体的效果。

一、社区发现概述

根据图论，加权网络表示为𝐺=(𝑉,𝐸,𝑊)，未加权网络表示为𝐺=(𝑉,𝐸)，其中𝑉和𝐸表示节点和边的集合，𝑊分别表示𝐸相应的权重，以连接的强度或容量为单位。在未加权的网络中，𝑊被视为1。子图𝑔⊆𝐺是保留原始网络结构的图划分。子图的划分遵循预定义（pre-define）的规则，不同的规则可能会导致不同形式的子图。
社区是代表真实社会现象的一种子图。换句话说，社区是一组具有共同特征的人或对象。
社区是网络中节点密集连接的子图，稀疏连接的节点沟通了不同的社区，使用𝐶={𝐶1,𝐶2,⋯,𝐶𝑘}表示将网络𝐺划分为𝑘个社区的集合，其中𝐶𝑖是社区划分的第𝑖个社区。
节点𝑣属于社区𝐶𝑖满足如下条件：社区内部每个节点的内部度大于其外部度。
因此，社区发现的目标是发现网络𝐺中的社区𝐶。

二、KL社区发现算法

K-L（Kernighan-Lin）算法是一种将已知网络划分为已知大小的两个社区的二分方法，它是一种贪婪算法，它的主要思想是为网络划分定义了一个函数增益Q，Q表示的是社区内部的边数与社区之间的边数之差，根据这个方法找出使增益函数Q的值成为最大值的划分社区的方法。
1、实现策略
该算法的具体策略是，将社区结构中的结点移动到其他的社区结构中或者交换不同社区结构中的结点。从初始解开始搜索，直到从当前的解出发找不到更优的候选解，然后停止。
首先将整个网络的节点随机的或根据网络的现有信息分为两个部分，在两个社团之间考虑所有可能的节点对，试探交换每对节点并计算交换前后的ΔQ，ΔQ=Q交换后-Q交换前，记录ΔQ最大的交换节点对，并将这两个节点互换，记录此时的Q值。
规定每个节点只能交换一次，重复这个过程直至网络中的所有节点都被交换一次为止。需要注意的是不能在Q值发生下降时就停止，因为Q值不是单调增加的，既使某一步交换会使Q值有所下降，但其后的一步交换可能会出现一个更大的Q值。在所有的节点都交换过之后，对应Q值最大的社团结构即被认为是该网络的理想社团结构。

地址：http://eda.ee.ucla.edu/EE201A-04Spring/kl.pdf
2、代码实现：

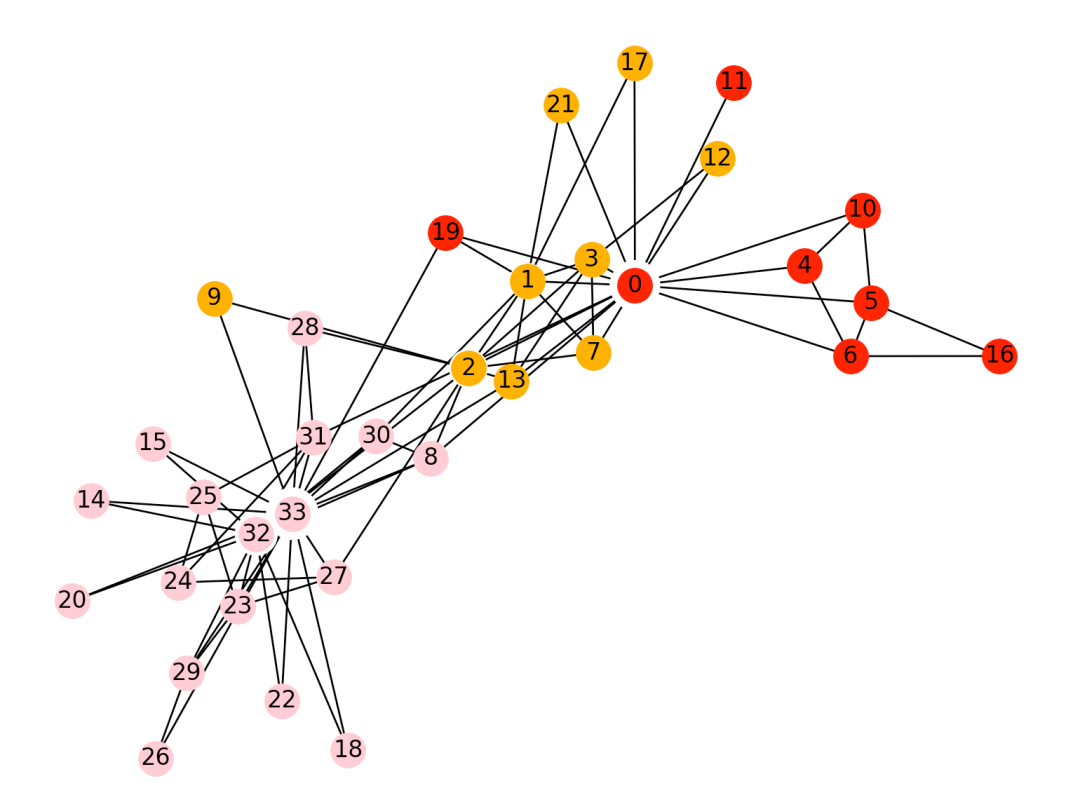
>>> def draw_spring(G, com):
...     pos = nx.spring_layout(G)  # 节点的布局为spring型
...     NodeId = list(G.nodes())
...     node_size = [G.degree(i) ** 1.2 * 90 for i in NodeId]  # 节点大小
...     plt.figure(figsize=(8, 6))  # 图片大小
...     nx.draw(G, pos, with_labels=True, node_size=node_size, node_color='w', node_shape='.')
...     color_list = ['pink', 'orange', 'r', 'g', 'b', 'y', 'm', 'gray', 'black', 'c', 'brown']
...     for i in range(len(com)):
...         nx.draw_networkx_nodes(G, pos, nodelist=com[i], node_color=color_list[i])
...     plt.show()
... 
>>> import networkx as nx
>>> import matplotlib.pyplot as plt
>>> G = nx.karate_club_graph()
>>> com = list(kernighan_lin_bisection(G))
>>> import matplotlib.pyplot as plt
>>> from networkx.algorithms.community import kernighan_lin_bisection
>>> com = list(kernighan_lin_bisection(G))
>>> print('社区数量', len(com))
社区数量 2
>>> draw_spring(G, com)

效果：

三、Louvain社区发现算法

Louvain算法是一种基于模块度的社区发现算法，其基本思想是网络中节点尝试遍历所有邻居的社区标签，并选择最大化模块度增量的社区标签，在最大化模块度之后，每个社区看成一个新的节点，重复直到模块度不再增大。
地址：https://arxiv.org/pdf/0803.0476.pdf
1、实现策略
具体实现上，如下图所示，步骤如下：
1)初始时将每个顶点当作一个社区，社区个数与顶点个数相同。
2)依次将每个顶点与之相邻顶点合并在一起，计算它们最大的模块度增益是否大于0，如果大于0，就将该结点放入模块度增量最大的相邻结点所在社区。
其中，模块度用来衡量一个社区的质量，公式第一如下。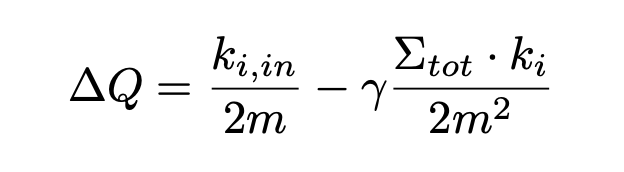

3）迭代第二步，直至算法稳定，即所有顶点所属社区不再变化。
4）将各个社区所有节点压缩成为一个结点，社区内点的权重转化为新结点环的权重，社区间权重转化为新结点边的权重。
5）重复步骤1-3，直至算法稳定。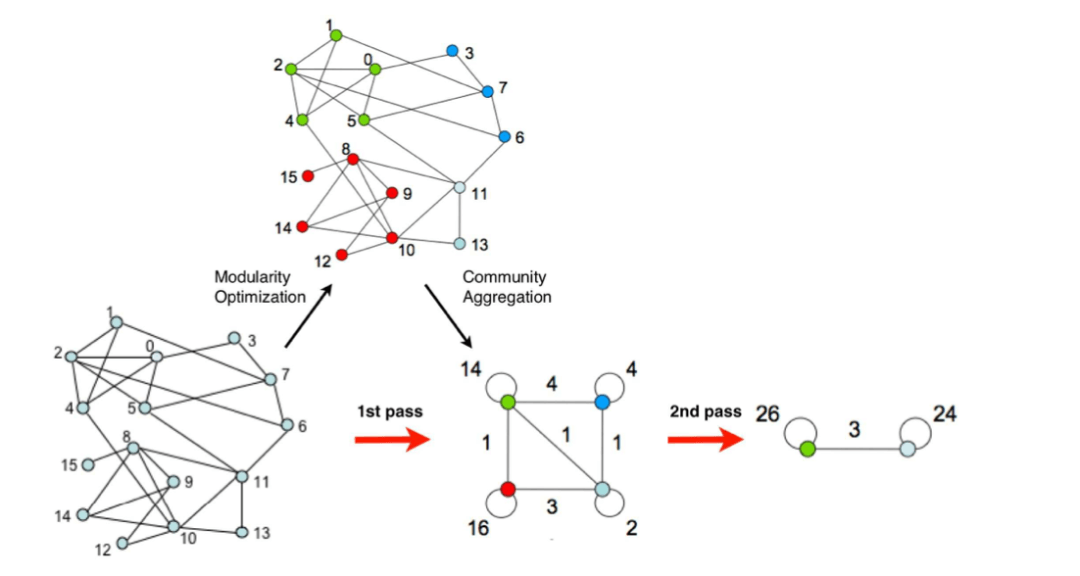

2、代码实现：

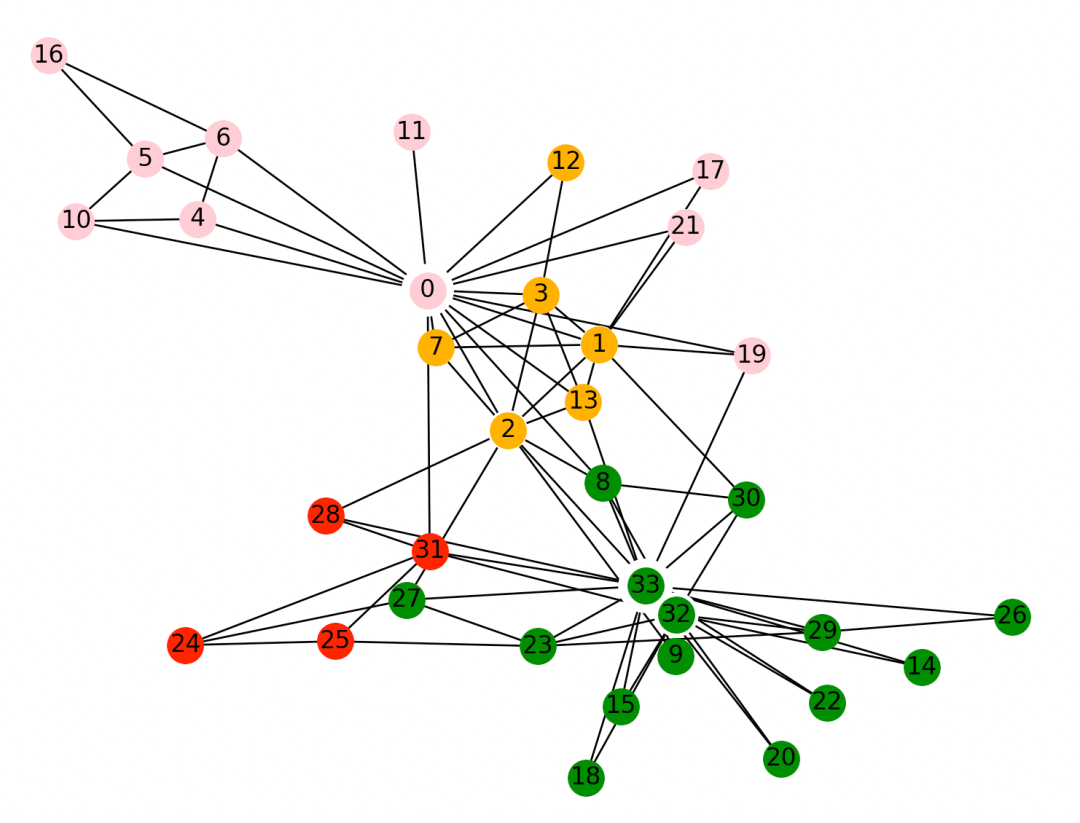
>>> import networkx as nx
>>> import matplotlib.pyplot as plt
>>> G = nx.karate_club_graph()
>>> com = list(kernighan_lin_bisection(G))
>>> import matplotlib.pyplot as plt
>>> from networkx.algorithms.community import louvain_communities
>>> com = list(louvain_communities(G))
>>> print('社区数量', len(com))
社区数量 4
>>> draw_spring(G, com)

3、效果：

四、标签传播社区发现算法

LPA全称label propagation algorithm，即标签传递算法，是一种图聚类算法，常用在社交网络中，用于发现潜在的社区，是一种基于标签传播的局部社区划分。对于网络中的每一个节点，在初始阶段，Label Propagation算法对于每一个节点都会初始化一个唯一的一个标签。
每一次迭代都会根据与自己相连的节点所属的标签改变自己的标签，更改的原则是选择与其相连的节点中所属标签最多的社区标签为自己的社区标签，这就是标签传播的含义，随着社区标签不断传播。最终，连接紧密的节点将有共同的标签
1、实现策略
LPA认为每个结点的标签应该和其大多数邻居的标签相同，将一个节点的邻居节点的标签中数量最多的标签作为该节点自身的标签（bagging思想）。给每个节点添加标签（label）以代表它所属的社区，并通过标签的“传播”形成同一个“社区”内部拥有同一个“标签”。
标签传播算法（LPA）的做法如下：
第一步: 为所有节点指定一个唯一的标签；
第二步: 逐轮刷新所有节点的标签，直到达到收敛要求为止。对于每一轮刷新，节点标签刷新的规则如下:
对于某一个节点，考察其所有邻居节点的标签，并进行统计，将出现个数最多的那个标签赋给当前节点。当个数最多的标签不唯一 时，随机选一个。
2、代码实现：

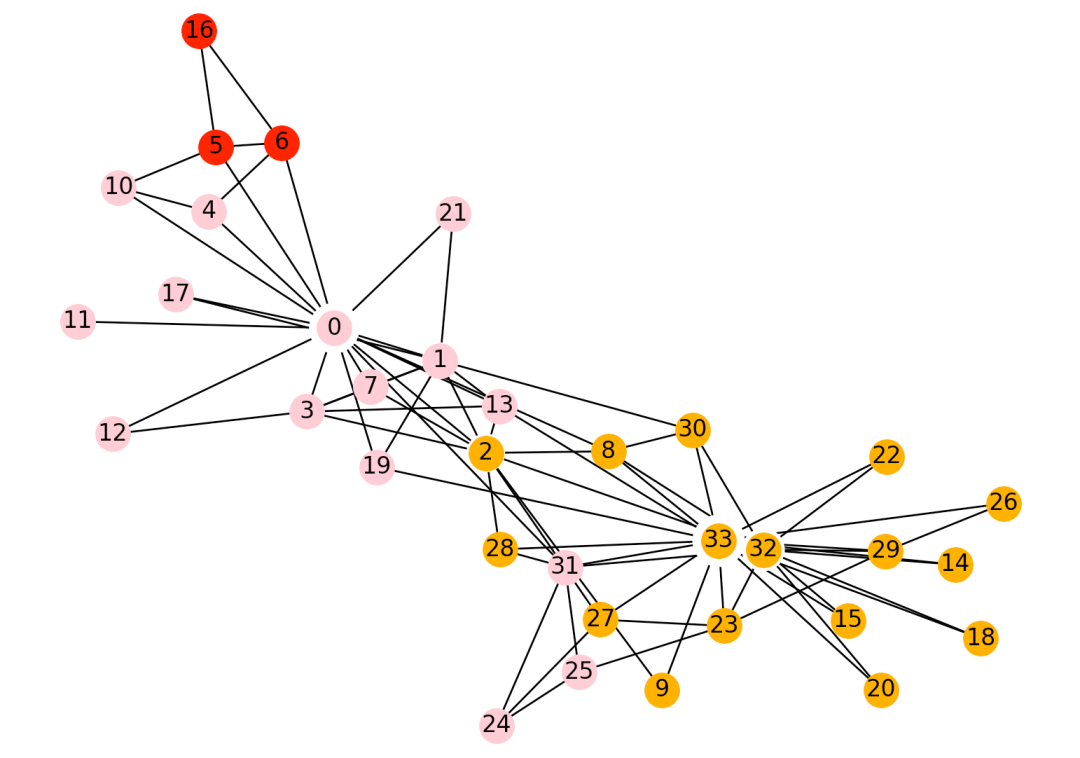
>>> import networkx as nx
>>> import matplotlib.pyplot as plt
>>> G = nx.karate_club_graph()
>>> com = list(kernighan_lin_bisection(G))
>>> import matplotlib.pyplot as plt
>>> from networkx.algorithms.community import label_propagation_communities
>>> com = list(label_propagation_communities(G))
>>> print('社区数量', len(com))
社区数量 3
>>> draw_spring(G, com)

3、效果

五、greedy_modularity社区算法

1、实现策略
贪心模块度社区算法，是一种用于检测社区结构的分层聚集算法，它在具有n个顶点和m条边的网络上的运行时间是O（mdlogn），其中d是描述社区结构的树状图的深度。

地址：https://arxiv.org/pdf/cond-mat/0408187v2.pdf
2、代码实现：

>>> import networkx as nx
>>> import matplotlib.pyplot as plt
>>> G = nx.karate_club_graph()
>>> com = list(kernighan_lin_bisection(G))
>>> import matplotlib.pyplot as plt
>>> from networkx.algorithms.community import greedy_modularity_communities
>>> com = list(greedy_modularity_communities(G))
>>> print('社区数量', len(com))
社区数量 3
>>> draw_spring(G, com)

3、效果：

参考文献

1、https://icode9.com/content-1-1321350.html
2、https://blog.csdn.net/qq_16543881/article/details/122825957
3、https://blog.csdn.net/qq_16543881/article/details/122781642

【2】社区发现之标签传播算法（LPA）

在Graph领域，社区发现（Community detection）是一个非常热门且广泛的话题，后面会写一个系列，该问题实际上是从子图分割的问题演变而来，在真实的社交网络中，有些用户之间连接非常紧密，有些用户之间的连接较为稀疏，连接紧密的用户群体可以看做一个社区，在风控问题中，可以简单的理解为团伙挖掘。
目前的社区发现问题分为两大类：非重叠社区发现和重叠社区发现。非重叠社区发现问题描述的是：一个网络中，每个节点均只能属于同一个社区，这意味这社区和社区之间是没有交集的。在非重叠社区发现算法中，有不同种类的解法：
1）基于模块度的社区发现算法：基本思想是通过定义模块度（Modularity）来衡量一个社区的划分是不是相对比较好的结果，从而将社区发现问题转化为最大化模块度的问题进行求解，后续的Louvain算法会讲到。
2）基于标签传播的社区发现算法：基本思想是通过标记节点的标签信息来更新未标记节点的标签信息，在整个网络中进行传播，直至收敛，其中最具代表性的就是标签传播算法（LPA,Label Propagation Algorithm），也是本文要讨论的算法。
注意：在团伙挖掘的实际应用的过程中，不要寄希望于优化社区发现算法提高准确性，可能永远都解决不了问题，因为关系的形成在实际中太过于复杂，我们更多的关注构图关系的筛选、清洗、提纯，以及分群后进一步加工处理

一、LPA概述

Label Propagation Algorithm，也称作标签传播算法（LPA），是一个在图中快速发现社群的算法，由Raghavan等人在2007年于论文《Near linear time algorithm to detect community structures in large-scale networks》中提出。在 LPA 算法中，节点的标签完全由它的直接邻居决定。标签传播算法是一种基于标签传播的局部社区发现算法，其基本思想是节点的标签（community）依赖其邻居节点的标签信息，影响程度由节点相似度决定，并通过传播迭代更新达到稳定。

1、算法的思想

在用一个唯一的标签初始化每个节点之后，该算法会重复地将一个节点的标签社群化为该节点的相邻节点中出现频率最高的标签。当每个节点的标签在其相邻节点中出现得最频繁时，算法就会停止。该算法是异步的，因为每个节点都会在不等待其余节点更新的情况下进行更新。
该算法有5个步骤：
1）初始化网络中所有节点的标签，对于给定节点x，Cx(0)=x。
2）设置 t=1。
3）以随机顺序排列网络中的节点，并将其设置为x。
4）对于特定顺序选择的每个x∈X，让Cx(t)=f(Cxi1(t)，…，Cxim(t)，…。f这里返回相邻标签中出现频率最高的标签。如果有多个最高频率的标签，就随机选择一个标签。
5）如果每个节点都有其邻居节点中数量最多的标签，则停止算法，否则，设置t=t+1并转到3。
这是一个迭代的计算过程且不保证收敛，大体的思路就是每个人都看看自己的邻居都在什么社区内，看看频率最高的社区是啥，如果和自己当前的社区不一样，就把这个最高频社区当成是自己的社区，然后告诉邻居，周而复始，直到对于所有人，邻居们告诉自己的高频社区和自己当前的社区是一样的，算法结束。所以说对于这个算法，计算复杂度是O(kE)，k是迭代的次数，E是边的数量。大家的经验是这个迭代的次数大概是5次就能近似收敛，以实现精度和性能的平衡，能发现这个数字和六度分隔理论里面的数字也差不多。
我们可以很形象地理解算法的传播过程，当标签在紧密联系的区域，传播非常快，但到了稀疏连接的区域，传播速度就会下降。当出现一个节点属于多个社群时，算法会使用该节点邻居的标签与权重，决定最终的标签，传播结束后，拥有同样标签的节点被视为在同一群组中。
下图展示了算法的两个变种：Push 和 Pull。其中 Pull 算法更为典型，并且可以很好地并行计算：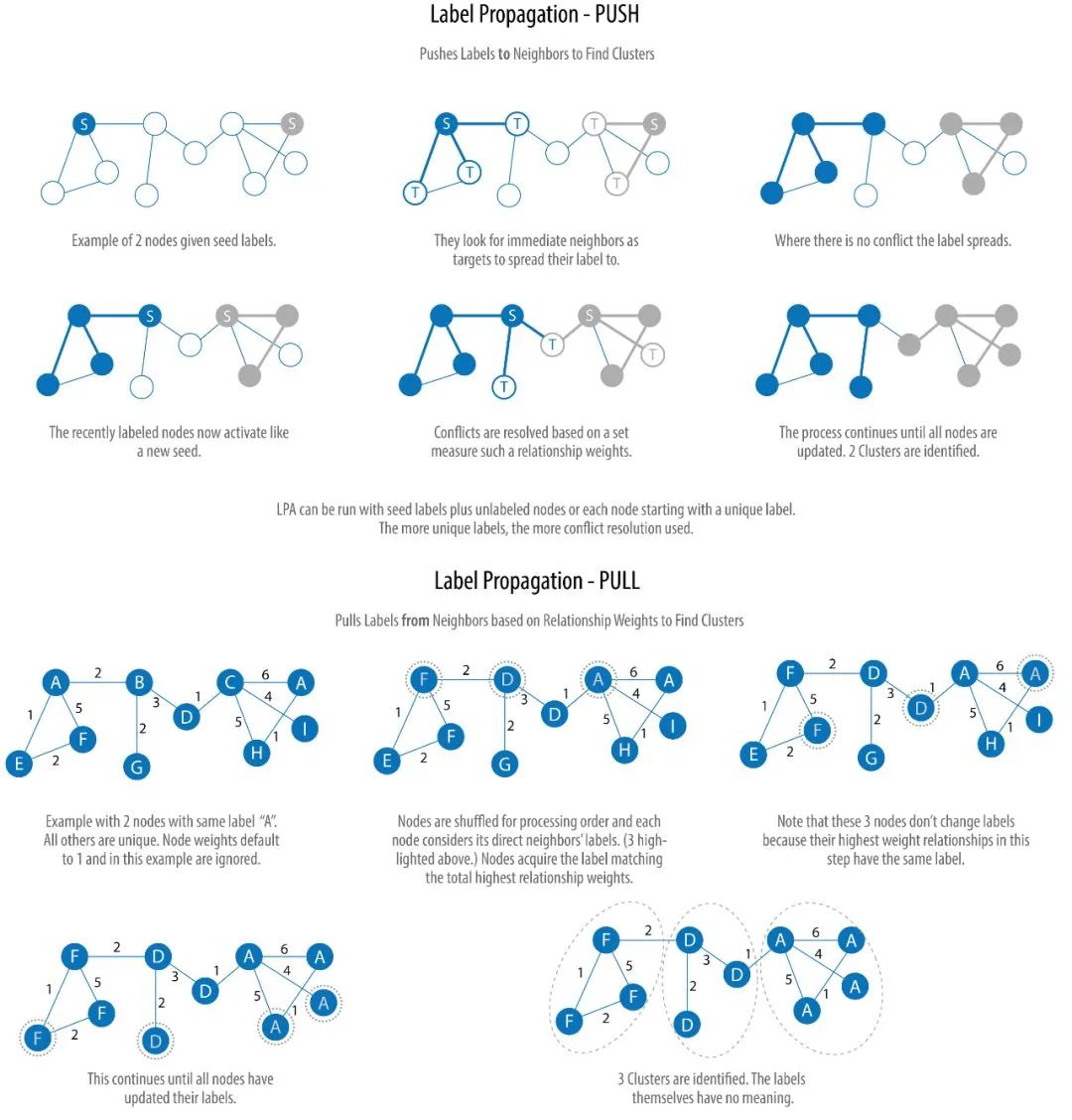

我们不再继续深入，看完上图，你应该已经理解了算法的大概过程。其实，做过图像处理的人很容易明白，所谓的标签传播算法，不过是图像分割算法的变种，Push 算法是区域生长法（Region Growing）的简化版，而 Pull 更像是分割和合并（divide-and-merge，也有人称 split-merge）算法。确实，图像（image）的像素和图（graph）的节点是十分类似的。

2、用于图聚类

图聚类是根据图的拓扑结构，进行子图的划分，使得子图内部节点的链接较多，子图之间的连接较少。依赖其邻居节点的标签信息，影响程度由节点相似度决定，并通过传播迭代更新达到稳定。
参考原始论文
https://arxiv.org/abs/0709.2938
https://arxiv.org/pdf/0709.2938.pdf
在算法开始之前为每个节点打上不同的标签，每一个轮次随机找到一个节点，查看其邻居节点的标签，找到出现次数最多的标签，随后将该节点改成该标签。当相邻两次迭代后社区数量不变或社区内节点数量不变时则停止迭代，下面看图解过程
初始化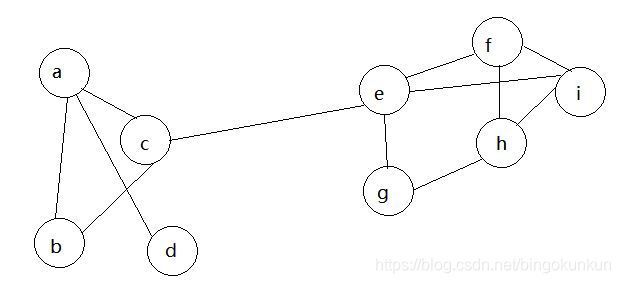

第一轮迭代
随机挑选一个节点（如c），发现其相邻节点有abe，三者出现次数相同，故随机选一个（如a），那么c点的标签被a替代。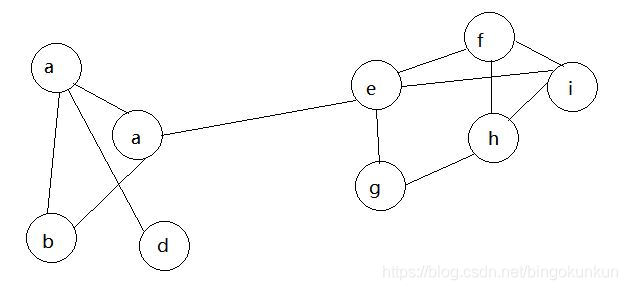

第二轮迭代
随机挑选一个节点（如b），发现其相邻节点均为a，故将b换成a，重复数次，最终的结果如图所示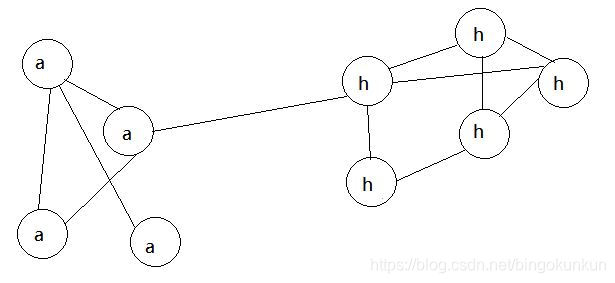

我们再看一个例子，比如下图：

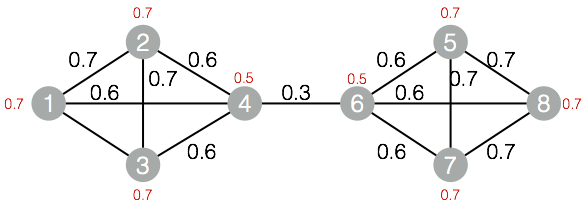
分组后的结果如下，我们得到了独立非重的groupid，这个结果其实是很难在实际场景中应用的，那么我们就的结果就没有意义了么？这个可以帮我们定位到浓度很高的群体，然后再加上部分属性标签，就能轻而易举的识别出问题黑产了。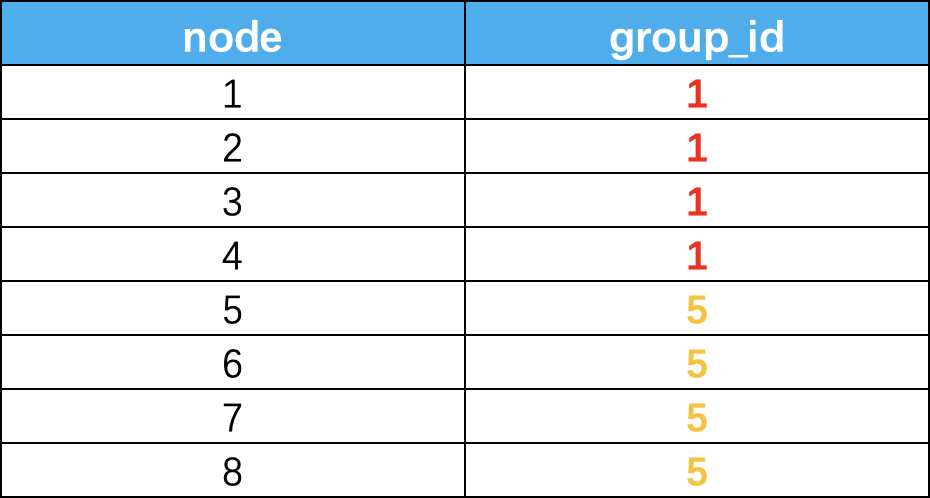

3、用于半监督

该算法也可以作为半监督的分类算法，标签传播时一种半监督机器学习算法，它将标签分配给以前未标记的数据点。在算法开始时，数据点的子集（通常只占很小一部分）有标签（或分类）。在整个算法过程中，这些标签会传播到未标记的点。在标签传播过程中，保持已标注数据的标签不变，使其像一个源头把标签传向未标注数据。
最终，当迭代过程结束时，相似节点的概率分布也趋于相似，可以划分到同一个类别中，从而完成标签传播过程，边的权重越大，表示两个节点越相似，那么label越容易传播过去。我们定义一个NxN的概率转移矩阵P：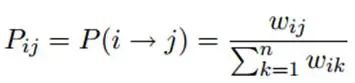

下面的图来看看传播过程

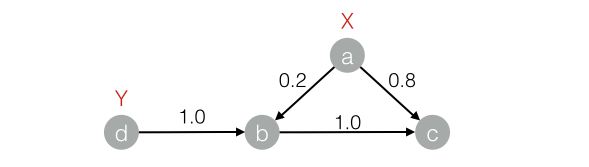
传播结束后的结果如下：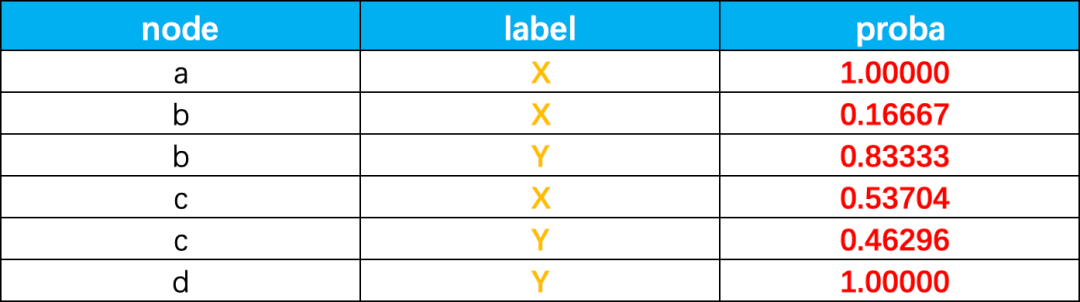

LPA使用已标记节点的标签作为基础，并尝试预测未标记节点的标签。然而，如果最初的标签是错误的，这可能会影响标签的传播过程，错误的标签可能会被传播。该算法是概率性的，并且发现的社区可能因执行的不同而不同。
**

二、算法代码实现

这个算法比较简单，有比较多的实现方式，最方便的还是networkx这个库，并用里面的一个简单的数据集进行试验。

1、数据集介绍

空手道数据集是一个比较简单的图数据集，下面我们看看其中的边和节点，后面应用这个数据集进行试验。

import networkx as nx
G = nx.karate_club_graph() # 空手道
G.nodes()
NodeView((0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33))
G.edges() 
EdgeView([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8),
(0, 10), (0, 11), (0, 12), (0, 13), (0, 17), (0, 19), (0, 21), (0, 31), 
(1, 2), (1, 3), (1, 7), (1, 13), (1, 17), (1, 19), (1, 21), (1, 30), 
(2, 3), (2, 7), (2, 8), (2, 9), (2, 13), (2, 27), (2, 28), (2, 32), 
(3, 7), (3, 12), (3, 13), (4, 6), (4, 10), (5, 6), (5, 10), (5, 16), 
(6, 16), (8, 30), (8, 32), (8, 33), (9, 33), (13, 33), (14, 32), 
(14, 33), (15, 32), (15, 33), (18, 32), (18, 33), (19, 33), (20, 32), 
(20, 33), (22, 32), (22, 33), (23, 25), (23, 27), (23, 29), (23, 32), 
(23, 33), (24, 25), (24, 27), (24, 31), (25, 31), (26, 29), (26, 33),
(27, 33), (28, 31), (28, 33), (29, 32), (29, 33), (30, 32), (30, 33),
(31, 32), (31, 33), (32, 33)])

2、自己实现LPA算法

import random
import networkx as nx
import matplotlib.pyplot as plt
  # 应该封装成类的形式
  def lpa(G):
      '''
      异步更新方式
      G：图
      return：None
      通过改变节点的标签，最后通过标签来划分社区
      算法终止条件：迭代次数超过设定值
      '''
      max_iter_num = 0 # 迭代次数
      while max_iter_num < 10:
          max_iter_num += 1
          print('迭代次数',max_iter_num)
          for node in G:
              count = {} # 记录邻居节点及其标签
              for nbr in G.neighbors(node): # node的邻居节点
                  label = G.nodes[nbr]['labels'] 
                  count[label] = count.setdefault(label,0) + 1
              #找到出现次数最多的标签
              count_items = sorted(count.items(),key=lambda x:-x[-1])
              best_labels = [k for k,v in count_items if v == count_items[0][1]]
              #当多个标签最大技术值相同时随机选取一个标签
              label = random.sample(best_labels,1)[0] # 返回的是列表，所以需要[0]
              G.nodes[node]['labels'] = label # 更新标签
  def draw_picture(G):
      # 画图
      node_color = [float(G.nodes[v]['labels']) for v in G]
      pos = nx.spring_layout(G) # 节点的布局为spring型
      plt.figure(figsize = (8,6)) # 图片大小
      nx.draw_networkx(G,pos=pos,node_color=node_color)
      plt.show()
  if __name__ == "__main__":
      G = nx.karate_club_graph() #空手道数据集
      # 给节点添加标签
      for node in G:
          G.add_node(node, labels = node) #用labels的状态
      lpa(G)
      com = set([G.nodes[node]['labels'] for node inG])
      print('社区数量',len(com))
      draw_picture(G)
迭代次数 1
迭代次数 2
迭代次数 3
迭代次数 4
迭代次数 5
迭代次数 6
迭代次数 7
迭代次数 8
迭代次数 9
迭代次数 10
社区数量 3

代码运行结果：

3、调包实现LPA算法

networkx集成了这个算法，可以直接调用

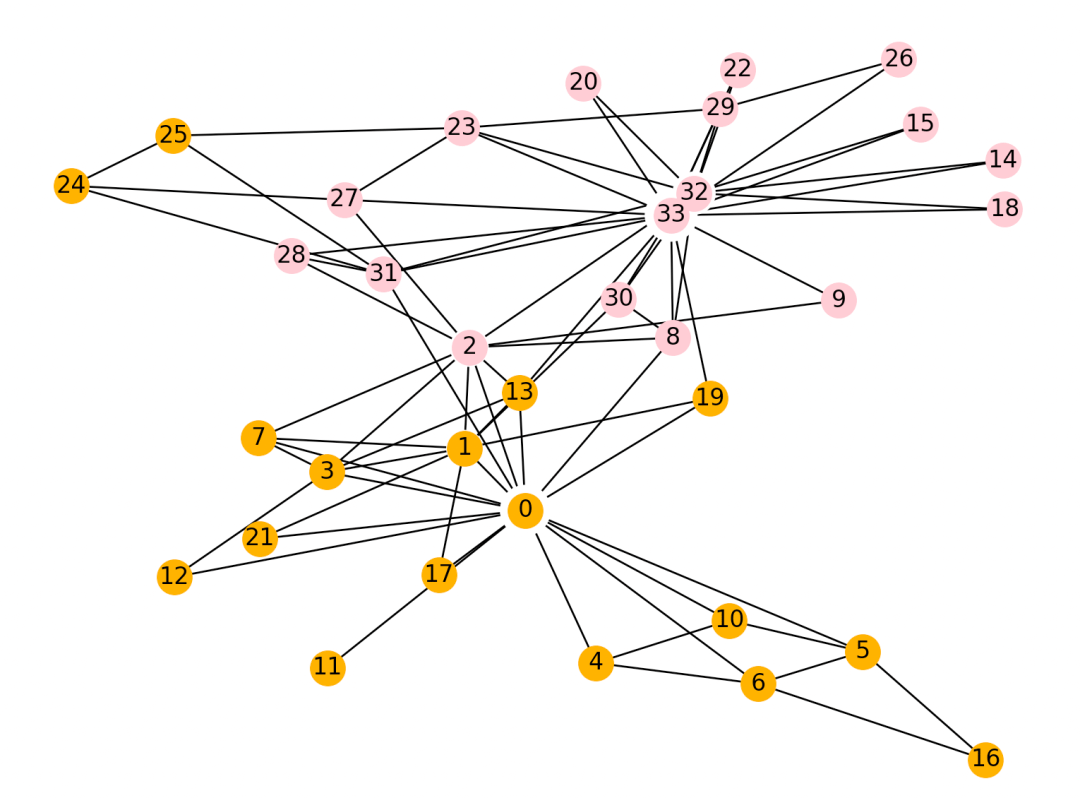
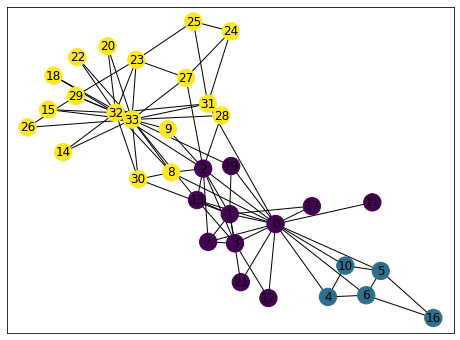
import matplotlib.pyplot as plt
import networkx as nx
from networkx.algorithms.community import asyn_lpa_communities as lpa
# 空手道俱乐部
G   = nx.karate_club_graph()
com = list(lpa(G))
print('社区数量',len(com))
com 
[{0, 1, 2, 3, 7, 8, 9, 11, 12, 13, 17, 19, 21, 30},
{4, 5, 6, 10, 16},
{14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 31, 32, 33}]
# 下面是画图
pos = nx.spring_layout(G) # 节点的布局为spring型
NodeId    = list(G.nodes())
node_size = [G.degree(i)**1.2*90 for i in NodeId] # 节点大小
plt.figure(figsize = (8,6)) # 设置图片大小
nx.draw(G,pos, 
        with_labels=True, 
        node_size =node_size, 
        node_color='w', 
        node_shape = '.'
       )
'''
node_size表示节点大小
node_color表示节点颜色
with_labels=True表示节点是否带标签
'''
color_list = ['pink','orange','r','g','b','y','m','gray','black','c','brown']
for i in range(len(com)):
    nx.draw_networkx_nodes(G, pos, 
                           nodelist=com[i], 
                           node_color = color_list[i+2],  
                           label=True)
plt.show()

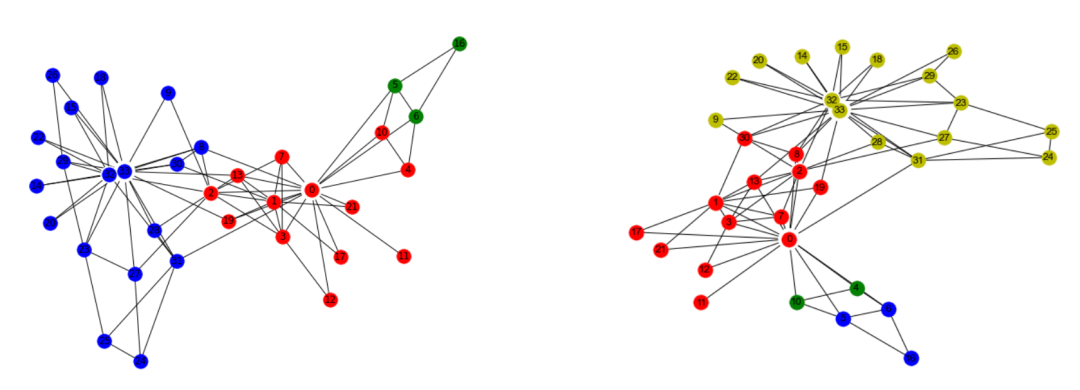
三、分群结果可视化

在可视化方面，确实R语言要强，大家有时间可以学习下，活儿全还是有点用处的，我们这里用R的igraph包来展现一些社区发现的结果。

library('igraph')
karate    <-  graph.famous("Zachary")
community <- label.propagation.community(karate)
# 计算模块度
modularity(community)
0.3717949
#membership查看每个点的各自分组情况。
membership(community)
1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 1 1 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2
plot(community,karate)

下面为两次跑的结果，可以看到，两次的结果并不一样，这个就是震荡效应导致的结果

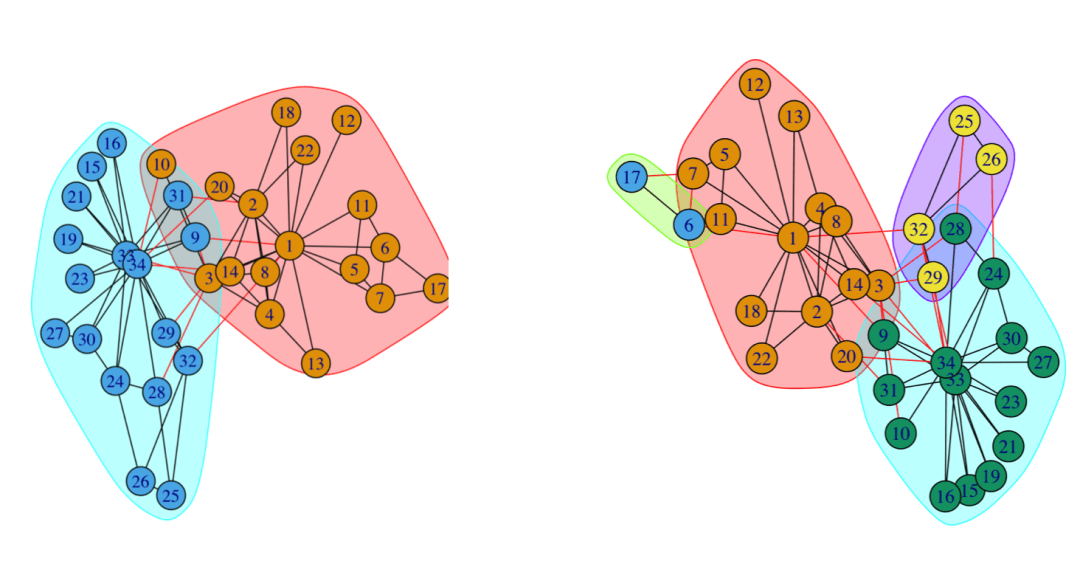
换一个对比下看看

community <- walktrap.community(karate,
                                weights = E(karate)$weight, 
                                steps = 8, 
                                merges =TRUE, 
                                modularity = TRUE)
plot(community,karate)

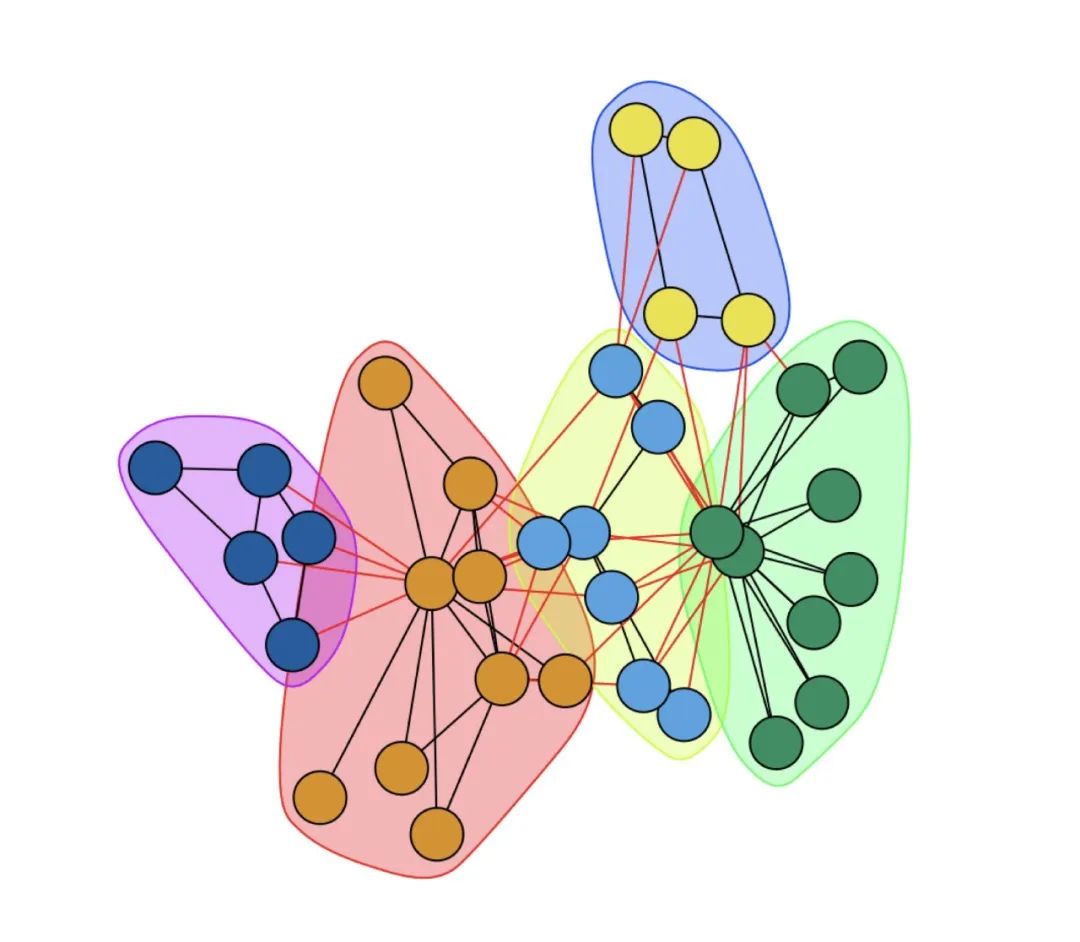
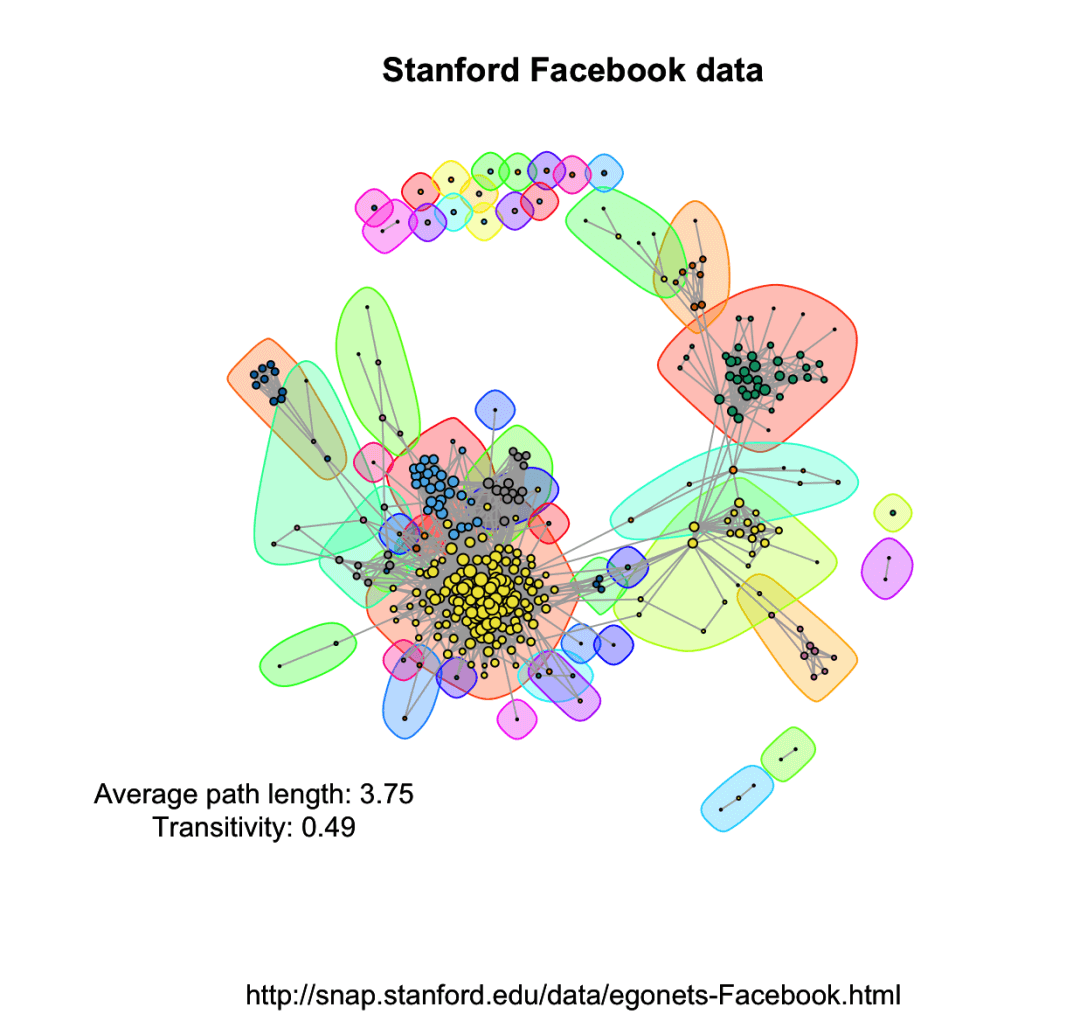
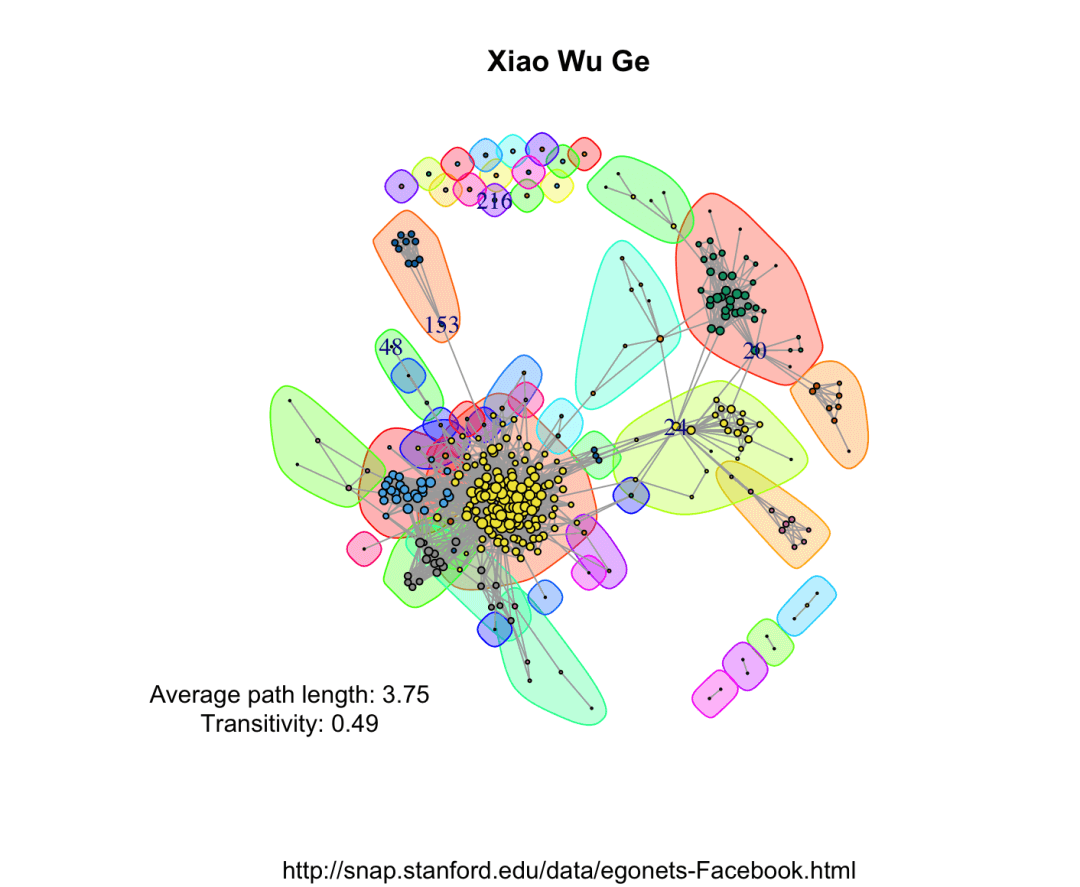
可以用更复杂的数据，画出来还挺好看的，数据集的下载地址：http://snap.stanford.edu/data/egonets-Facebook.html

library(igraph)
library(d3Network)
igraphDat <- read.graph(file = "/Users/wuzhengxiang/Documents/PPT模板/0.edges", directed = FALSE)
## Simplify to remove duplications and from-self-to-self loops
igraphDat <- simplify(igraphDat, 
             remove.multiple = TRUE, 
             remove.loops = TRUE
             )
## Give numbers
V(igraphDat)$label <- seq_along(V(igraphDat))
## Average path length between any two given nodes
(averagePathLength <- average.path.length(igraphDat))
## Community structure detection based on edge betweenness
communityEdgeBetwn <- edge.betweenness.community(igraphDat)
## Check the transitivity of a graph (probability that the adjacent vertices of a vertex are connected)
(transitivityDat <- transitivity(igraphDat, 
             type = "localaverage",
             isolates = "zero")
             )
## Set the seed to get the same result
set.seed("20200513")
## Add community indicating background colors
plot(igraphDat,
vertex.color = communityEdgeBetwn$membership, 
vertex.size = log(degree(igraphDat) + 1),
mark.groups = by(seq_along(communityEdgeBetwn$membership), 
communityEdgeBetwn$membership, invisible)
    )
## Annotate
title("Stanford Facebook data", 
      sub = "http://snap.stanford.edu/data/egonets-Facebook.html"
     )
text(x = -1, y = -1, 
     labels = sprintf("Average path length: %.2f\nTransitivity: %.2f",
                      averagePathLength, 
                      transitivityDat)
    )

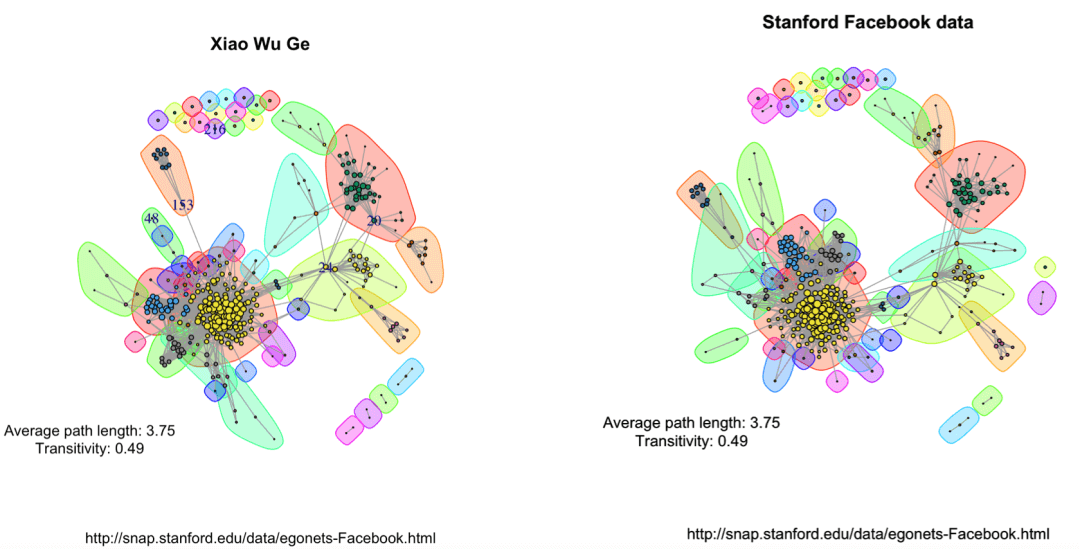
四、算法优缺点

作为一个比较简单的算法，其优缺点也是特别的明显。

1、算法优点

算法逻辑简单，时间复杂度低，接近线性复杂度，在超大规模网络下会有优异的性能，适合做社区发现的baseline。
无须定义优化函数，无须事先指定社区个数，算法会利用自身的网络结构来指导标签传播。

2、算法缺点

雪崩效应：社区结果不稳定，随机性强。由于当邻居节点的社区标签权重相同时，会随机取一个。导致传播初期一个小的错误被不断放大，最终没有得到合适的结果。尤其是异步更新时，更新顺序的不同也会导致最终社区划分结果不同。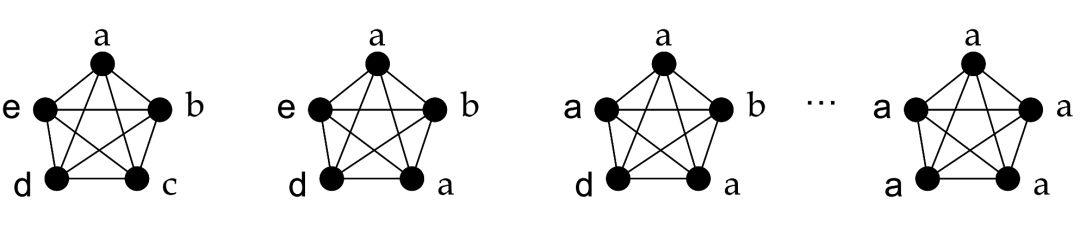

上图中展示了一次标签传播算法的流程：初始化阶段，每个节点都以自己作为社区标签。比如a的社区就是a，c的社区就是c。当进入传播阶段，节点c的邻居节点共4个：a，b，c，d。而社区标签也是4个：a，b，c，d，假设随机取了一个a。
如果是异步更新，此时b，d，e三个节点的邻居节点中社区标签均存在2个a，所以他们都会立马更新成a。如果c当时随机选择的是b，那么d,e就会更新成b，从而导致b社区标签占优，而最终的社区划分也就成b了。
震荡效应：社区结果来回震荡，不收敛，当传播方式处于同步更新的时候，尤其对于二分图或子图存在二分图的结构而言，极易发生。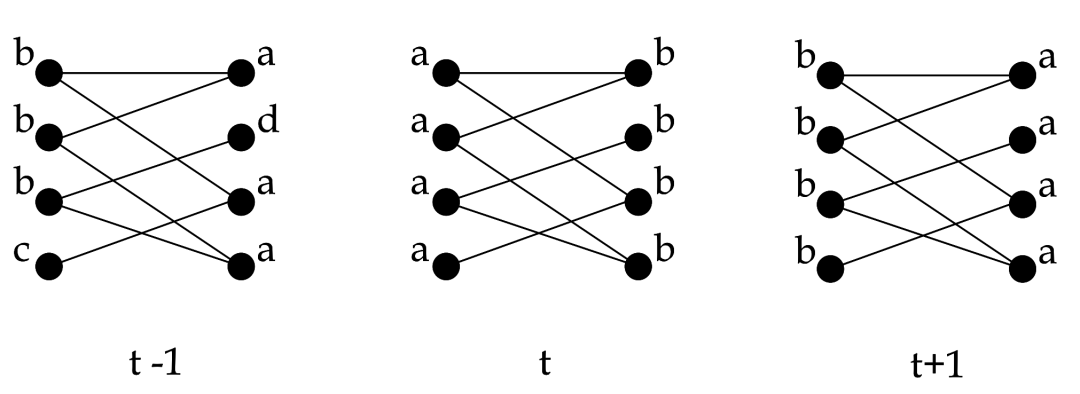

上图中展示了一次二分图中标签传播算法的流程，在同步更新的时候，每个节点依赖的都是上一轮迭代的社区标签。当二分图左边都是a，右边都是b时，a社区的节点此时邻居节点都是b，b社区的节点此时邻居节点都是a，根据更新规则，此时a社区的节点将全部更新为b，b社区的节点将全部更新为a。此时算法无法收敛，使得整个网络处于震荡中。

【3】万物皆网络，万字长文详解社区发现算法Louvain

大家好，我是小伍哥，好久没更新，今天发一篇社区发现（community detection）的文章，文章靠几十篇文章拼拼凑凑而成，也就不标原创了，不过我也写了很多观点进去，还是非常好的参考学习资料。
所谓的社群发现，通俗点，可以叫团伙挖掘，是风控工作中非常核心的算法，我上次也写过一篇LPA的，今天再写一篇Louvain算法相关的，如果你就是想调个包，那直接跳到第八部分就行，如果想认真的了解下，那就从头开始。
注意：我一直认为，在团伙挖掘的过程中，介质的质量、边的构建思路、以及业务的抽象能力，比什么算法都重要，盲目的在质量不高的数据上，啥算法都没用。
一、社区发现概述
1、社区是什么
2、社区发现的目标和意图
3、节点间存在连接的抽象本质 - 逻辑拓朴结构
4、什么时候可以使用社区发现算法
5、社区划分的直观思路
二、什么是模块度

三、模块度最大化算法
1、算法流程
2、怎么表示一个随机图

四、Louvain 算法
1、不同密度社区对比
2、社区发现效果评估-模块化指数Q
3、社区发现算法-Louvain

五、基本概念—权重度
1、节点权重度
2、社区权重度
3、社区内部权重度
4、全图权重度

六、基本概念—社区压缩
1、什么是社区压缩？
2、为什么要进行社区压缩

七、Louvain算法结果处理

八、Louvain算法应用

一、社区发现概述

1、社区是什么

在最常见的社交网络中，每个用户相当一个点，用户之间的互相关注、点赞、私信等形成了边，用户以及相互作用关系构成了一个大的关系网络。
在这样的网络中，有的用户之间的连接较为紧密，有的用户之间的连接关系较为稀疏。其中连接较为紧密的部分可以被看成一个社区，其内部的节点之间有较为紧密的连接，而在两个社区间则相对连接较为稀疏，整个整体的结构被称为社团结构，如下图，红色的黑色的点集呈现出社区的结构。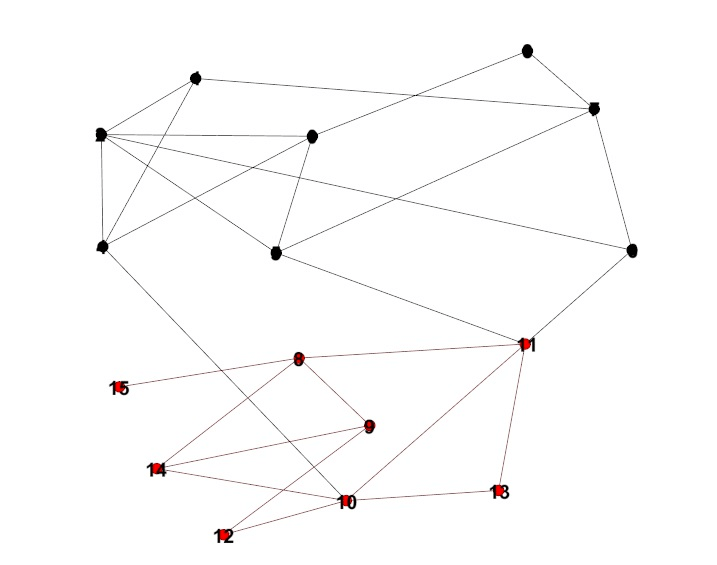

用红色的点和黑色的点对其进行标注，整个网络被划分成了两个部分，其中，这两个部分的内部连接较为紧密，而这两个社区之间的连接则较为稀疏。如何去划分上述的社区便称为社区划分的问题。

2、社区发现的目标和意图

社区发现的目标是什么？我们为什么要去做社区发现？。社区发现的目的也很简单，就是在图中找到一些“潜在的有特定关系的组织”，也就是社区(community)。直观地说，社区发现（community detection）的一般目标是要探测网络中较为紧密的【块cluster】或是【社团community】。
这么做的目的和效果有许多，特别是在风控中，很多有目的的团伙，聚集在一起，有明显的社群关系。哪个块是高风险，哪个块是高价值，非常值得挖掘。
我们再看一个例子，词的联想和搭配构成的网络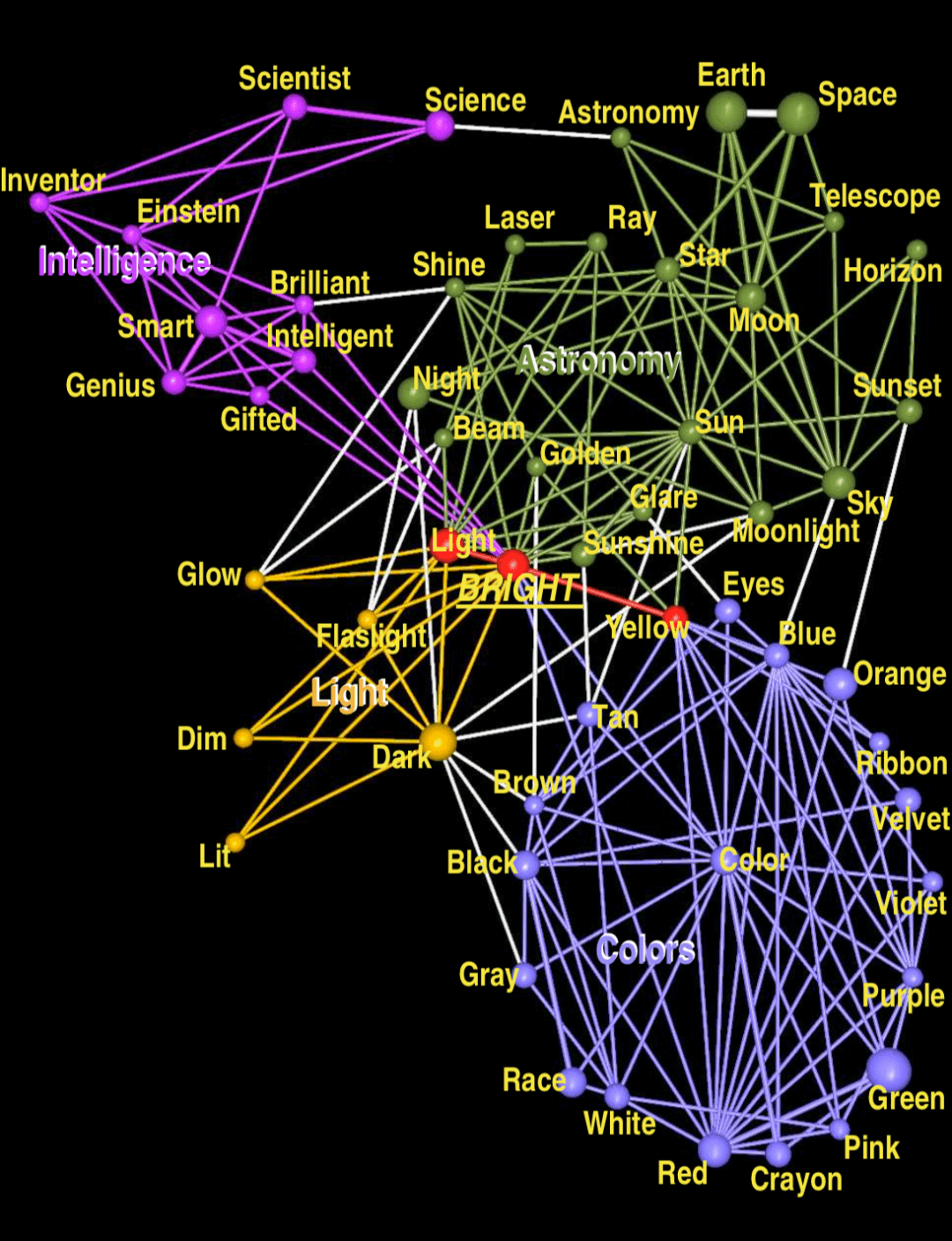

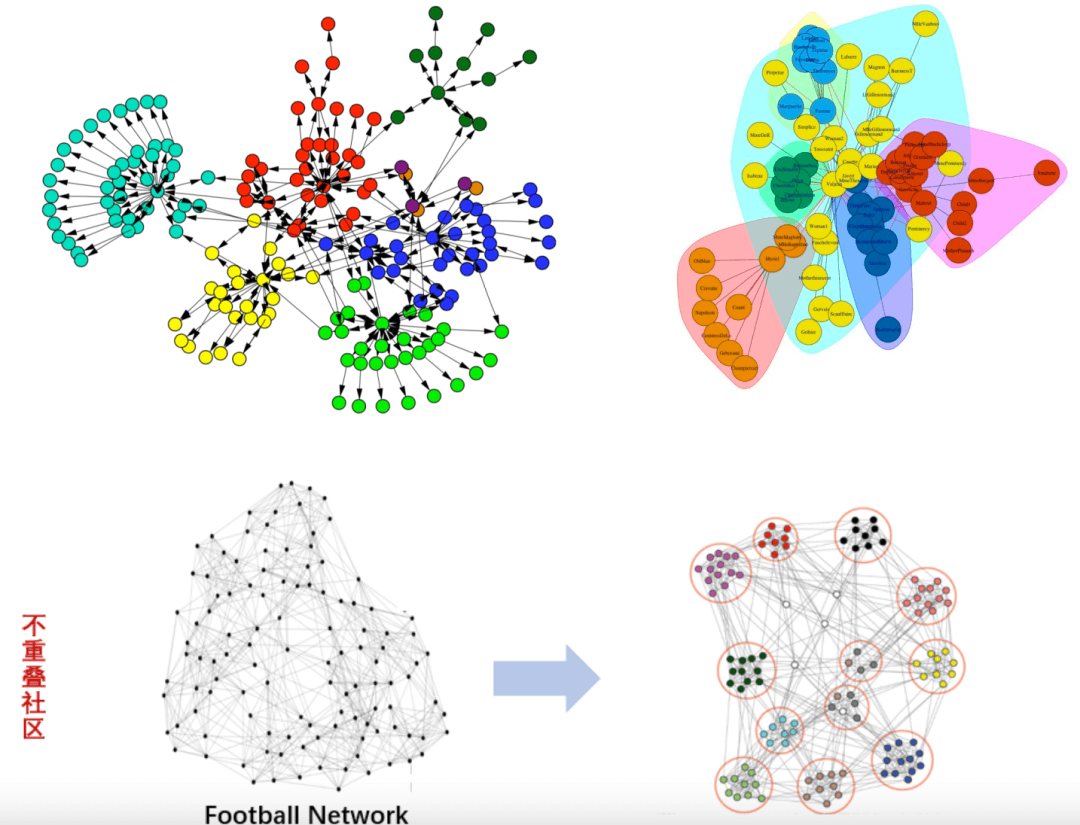
我们用不同的颜色对community进行标记，可以看到这种检测得到的结果很有意思。这个网络从词bright开始进行演化，到后面分别形成了4个组：Colors, Light, Astronomy & Intelligence。
可以说以上这4个词可以较好地概括其所在community的特点（有点聚类的感觉）；另外，community中心的词，比如color, Sun, Smart也有很好的代表性（自动提取摘要）。
同时我们注意到，那些处在交叠位置的词呢，比如Bright、light等词，他们是同义项比较多的词。这个图也揭示出了这一层含义。

3、节点间存在连接的抽象本质 - 逻辑拓朴结构

社区的节点间是网络拓朴结构，即节点间是存在拓朴连接结构的，我们不能将其和欧式空间或者P空间中的点向量集合空间混为一谈。
以欧式空间为例，不同的节点向量存在于不同的空间位置中，向量夹角近的点向量彼此距离近，而向量夹角远的向量彼此距离远。但是即使是欧式距离很近的向量点，也不一定就代表这它们之间存在拓朴连接关系，只能说在一定的度量下（例如欧式距离度量），这两个节点很相近。
但是在社区结构中，节点之间没有什么空间位置的概念。相对的，节点间存在的是一种逻辑拓朴结构，即存在一种共有关系。
存在共有关系的节点在逻辑上会聚集为一个社区，而社区之前不存在或者存在很弱的共有关系，则呈现分离的逻辑拓朴结构。
一定要注意不要用空间结构的概念来试图理解社区结构，不然会陷入理解的困境，并且会限制想象力，社区中的节点只是因为逻辑上的共有关系而聚集在一起而已，彼此之间的位置也没有实际意义，而社区族群之间的分离也是表达一种逻辑上的弱共有关系。举一些实际的例子：
1） 假如节点代表消费者：节点间的连接代表了它们共同购买了一批书籍，权重代表共同购买的书籍数，链接越紧密，代表社群的爱好越相近。
2） 假如节点代表消费者：节点间的连接代表了它们共同领取一批优惠群，权重代表共同领取的优惠券的数量，该社群可能是一个羊毛党社群。
3） 假如节点代表商家：节点间的连接代表了它们共同商品标题，权重代表共同标题商品的数量，该社群可能是一个店群商家，不断换点进行欺诈。
共同的地点、共同的设备、共同的轨迹、共同的时间、共同的证件等等，都可以作为这种逻辑关系的存在，作为一个网络，我们进行社区挖掘，达到我们的业务目的。

4、什么时候可以使用社区发现算法

下面这句话很明确地说明了在什么业务场景下可以使用社区发现算法：我们需要先确定要解决的业务场景中，存在明显的聚集规律，节点（可以是抽象的）之间形成一定的族群结构，而不是呈现无规律的随机分散。同时另一方面，这种聚集的结构是“有意义的”，这里所谓的有意义是指这种聚集本身可以翻译为一定的上层业务场景的表现。
但是很多时候，我们业务场景中的数据集之间的共有关系并不是表现的很明显，即节点之间互相都或多或少存在一些共有关系，这样直接进行社区发现效果肯定是不好的。就没必要进行社区发现挖掘。
所以一个很重要点是，我们在进行社区发现之前，一定要进行数据降噪。理想情况下，降噪后得到的数据集已经是社区完全内聚，社区间完全零连接，这样louvain只要一轮运行就直接得到结果。当然实际场景中不可能有这么好的情况，数据源质量，专家经验的丰富程度等等都会影响降噪的效果，一般情况下，降噪只要能cutoff 90%以上的噪音，louvain就基本能通过几轮的迭代完成整体的社区发现过程。

5、社区划分的直观思路

什么样的结构能成为团？一种很直观的想法是，同一团内的节点连接更紧密，即具有更大的density。
接下来的问题是，什么样的metrics可以用来描述这种density？Louvian 定义了一个数值上的概念（本质上就是一个目标函数），有了这个目标函数，就可以引出接下来要讨论的 method based on modularity optimization
要注意的，社区划分有很多不同的算法，本文讨论的 Fast Unfolding（Louvian）只是其中一种，而这种所谓的density密度评估方法也其实其中一种思想，不要固话地认为社区划分就只有这一种方法。

关于社区发现算法可以应用在哪些领域，或者在风控中能用于什么场景，我也一直在思考中，从这个算法的思想上来看，我倾向于认为社区发现算法比较适合发现一种”抽象泛共现模式”，这种共现是一种泛化的共现，它可以是任何形式的共现，例如
1）两个用户拥有共同的介质
2）两个用户昵称采用共同的起名方式，比如名字加数字，同样的前缀，或者都是四字成语等
3）用户拥有相同的行为，比如做过同样的操作，
4）用户拥有共同的控制人等
5）两个用户发布的内容拥有相似的词频数据
6）两个用户拥有相同的运动轨迹
… …
社区发现的落地效果，很大程度上，取决于我们对业务拓扑逻辑的抽象水平，以及数据降噪的结果，而不取决于发现的算法。并且不同场景，采用的社区发现算法不一样。在大数据场景下，没有上帝全局视角，并且很多常识在规模面前也不管用，甚至引起认知谬误，因此社区发现算法的结果不可能完美，必须结合业务实际情况进行调节和控制，再应用，不然很难达到预期效果，甚至搞出很多问题。

二、什么是模块度

在各类网络中会存在一些紧密连接的区域，这些区域（节点集）通常有自己的属性，称为社群或者社团（Community），社团内部连接紧密，而社团外部的连接则相对稀疏，即“内紧外松”，根据这个特点，人们设计了算法来探测网络中的社团结构，从而更好地理解网络中蕴含的丰富信息。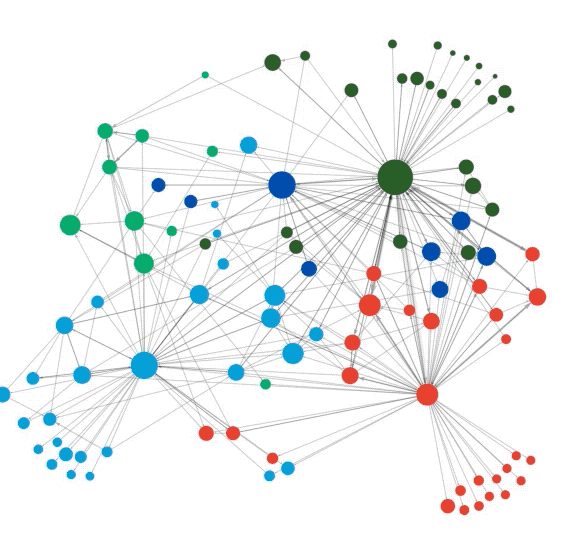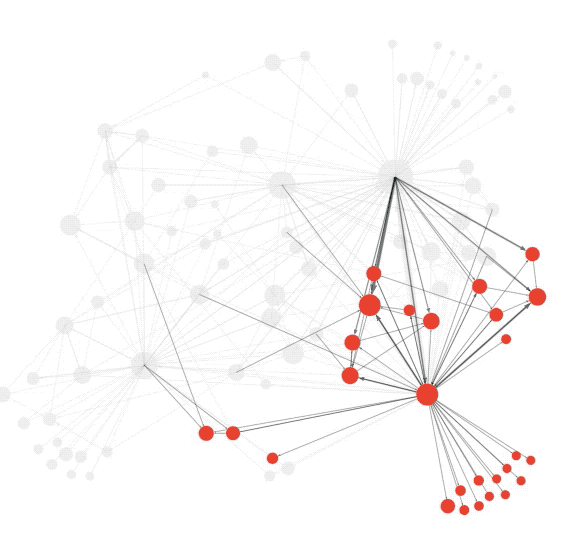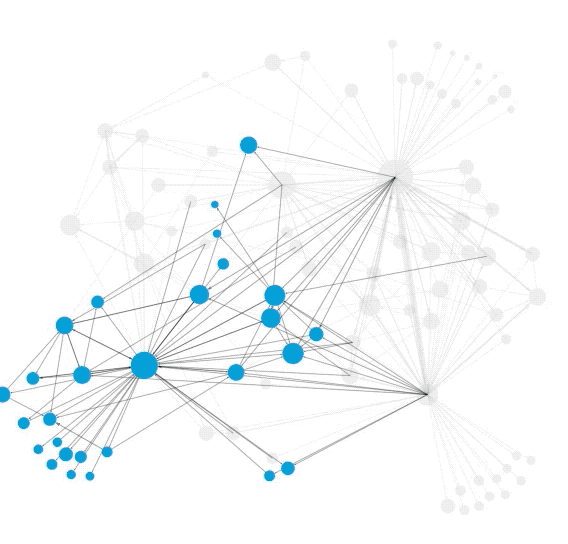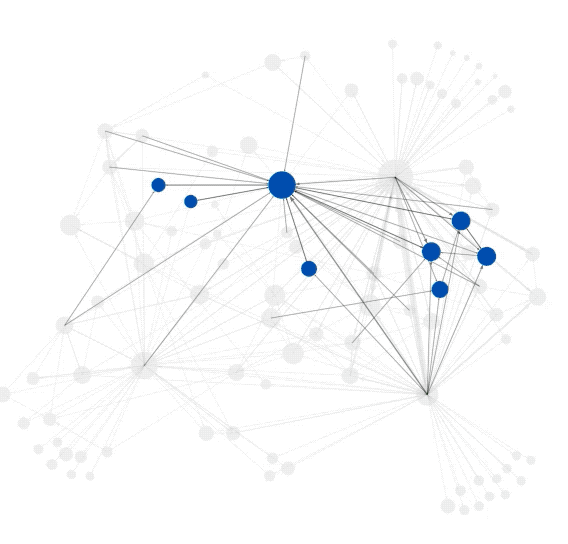

“社群检测”等同于“给节点分组”，模块度（Modularity）是一种常用的衡量节点分组质量的标准，模块度越高说明所检测到的社团越符合“内紧外松”的特征，分组质量越好。

基于模块度的概念，网络科学奠基人之一Mark Newman于2004年提出了一种经典的社团检测方法—模块度最大值法（Modularity maximization）。它通过考虑网络中所有可能的节点分组，找到使得模块度最大的分组方式。基于模块度的社团检测算法至今仍被广泛使用。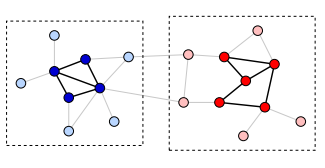

要计算一个网络的模块度，需要构造一个具有相同节点度分布的随机网络作为参照。通俗地来说，模块度的物理含义是：在社团内，实际的边数与随机情况下的边数的差距。如果差距比较大，说明社团内部密集程度显著高于随机情况，社团划分的质量较好。模块度取值范围在[-0.5,1]之间。如果节点组中的连边数量超过了随机分配时所得到的期望连边数量，模块度为正数。没有超过，则为负数。

三、模块度最大化算法

模板度最大值法是使用最为广泛的社团检测方法之一，该方法的目标是从所有可能的分组中找到使得模块度最大的分组，由于穷举所有可能的分组十分困难，所以实际的算法都采用近似优化方法。例如，Mark Newman 提出了模块度最大化的贪婪算法 Fast NewMan (FN)。贪婪算法的原理是找出每个局部最优值，最终将局部最优值整合成整体的近似最优值。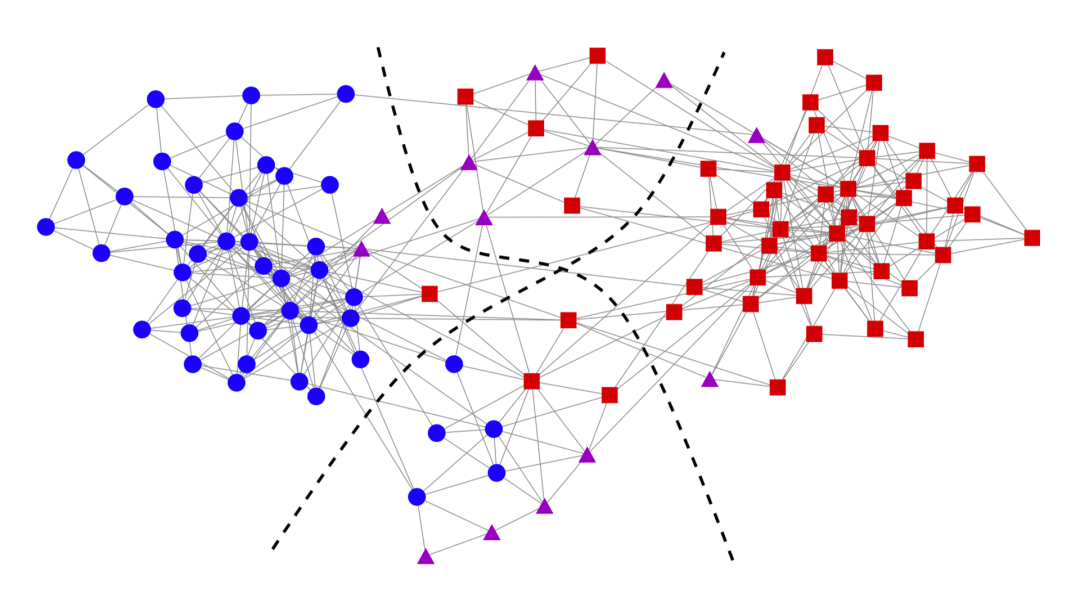

模块度是评估一个社区网络划分好坏的度量方法，它的物理含义是社区内节点的连边数与随机情况下的边数之差，它的取值范围是 [−1/2,1)，其定义如下：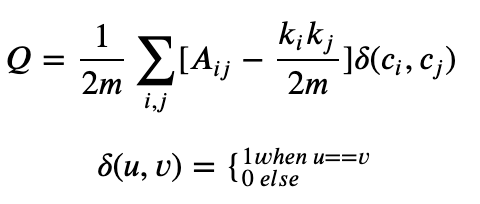

其中，𝐴𝑖𝑗节点i和节点j之间边的权重，网络不是带权图时，所有边的权重可以看做是1；𝑘𝑖=∑𝑗𝐴𝑖𝑗表示所有与节点i相连的边的权重之和（度数）；𝑐𝑖表示节点i所属的社区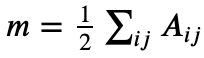；表示所有边的权重之和（边的数目）。公式中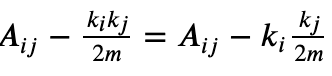

节点j连接到任意一个节点的概率是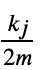，现在节点i有𝑘𝑖的度数，因此在随机情况下节点i与j的边为.
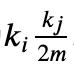模块度的公式定义可以作如下简化：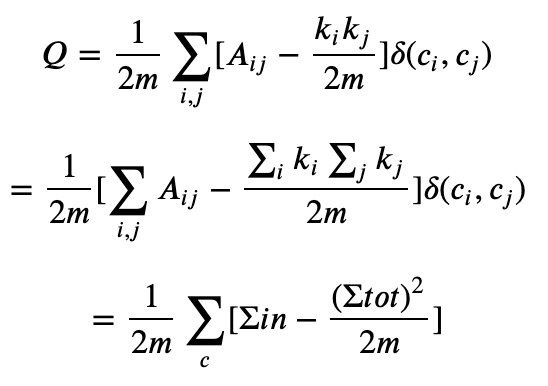

其中Σ𝑖𝑛Σin表示社区c内的边的权重之和，Σ𝑡𝑜𝑡Σtot表示与社区c内的节点相连的边的权重之和。上面的公式还可以进一步简化成: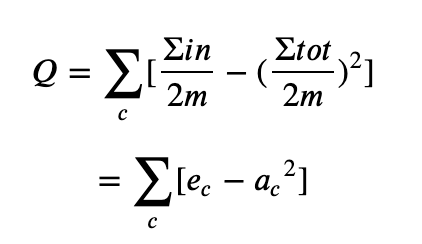

这样模块度也可以理解是社区内部边的权重减去所有与社区节点相连的边的权重和，对无向图更好理解，即社区内部边的度数减去社区内节点的总度数。基于模块度的社区发现算法，都是以最大化模块度Q为目标。

1、算法流程

Louvain算法的思想很简单：
1）将图中的每个节点看成一个独立的社区，次数社区的数目与节点个数相同；
2）对每个节点i，依次尝试把节点i分配到其每个邻居节点所在的社区，计算分配前与分配后的模块度变化Δ𝑄，并记录Δ𝑄最大的那个邻居节点，如果𝑚𝑎𝑥Δ𝑄>0，则把节点i分配Δ𝑄最大的那个邻居节点所在的社区，否则保持不变；
3）重复2），直到所有节点的所属社区不再变化；
4）对图进行压缩，将所有在同一个社区的节点压缩成一个新节点，社区内节点之间的边的权重转化为新节点的环的权重，社区间的边权重转化为新节点间的边权重；
5）重复1）直到整个图的模块度不再发生变化。
从流程来看，该算法能够产生层次性的社区结构，其中计算耗时较多的是最底一层的社区划分，节点按社区压缩后，将大大缩小边和节点数目，并且计算节点i分配到其邻居j的时模块度的变化只与节点i、j的社区有关，与其他社区无关，因此计算很快。在论文中，把节点i分配到邻居节点j所在的社区c时模块度变化为：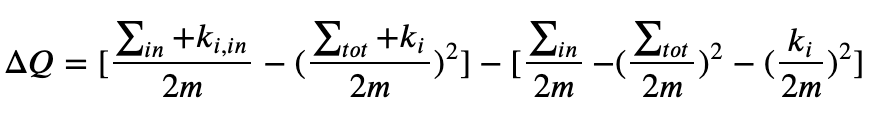

其中𝑘𝑖,𝑖𝑛是社区c内节点与节点i的边权重之和，注意对𝑘𝑖,𝑖𝑛是对应边权重加起来再乘以2，这点在实现时很容易犯错。
Δ𝑄分了两部分，前面部分表示把节点i加入到社区c后的模块度，后一部分是节点i作为一个独立社区和社区c的模块度，这里有一个困惑我的地方，虽然我按照这个公式实现的分群算法效果很好，但是我认为Δ𝑄少了把节点i从其原来社区删除这一步，因为后面的划分时，节点i所在的社区可能有多个节点。
在实现的时候模块度变化还可以简化，把上面的公式展开，很多项就抵消了，化简之和：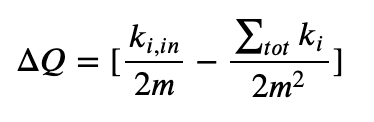

论文中指出，算法第2）步节点的顺序会对分群结果又一定影响，但分群效果差距不大，只是会影响算法的时间效率，还有论文指出按度数从到的小的顺序处理速度最快，不过我在1K边上的图测试，差距不大。

1）初始时将网络中的每个节点都看成独立的小社团。
2）考虑所有相连社团两两合并的情况，计算每种合并带来的模块度的增量。
3）基于贪婪原则，选取使模块度增长最大的两个社团，将它们合并成一个社团。
4）如此循环迭代。随着迭代的进行，模块度不断变化，其最大值时对应最优社团划分。

后来，Vincent Blondel等人运用模板度最大值法的基本原理，提出了Louvain算法，大大降低了算法的时间复杂度。十分适合社会网络等超大规模网络的社团检测。也成为应用最广的算法之一。使用Python的网络科学工具包NetworkX , 可以轻松调用该算法，实现社团检测。

NetworkX：是Python在复杂网络分析领域的软件包，网络分析的必备神器，谁用谁知道。它功能强大，几乎覆盖复杂网络分析中的所有可计算的概念。小伙伴们只要会使用Python进行基本编程，就可以用起来。

官网地址：
https://networkx.github.io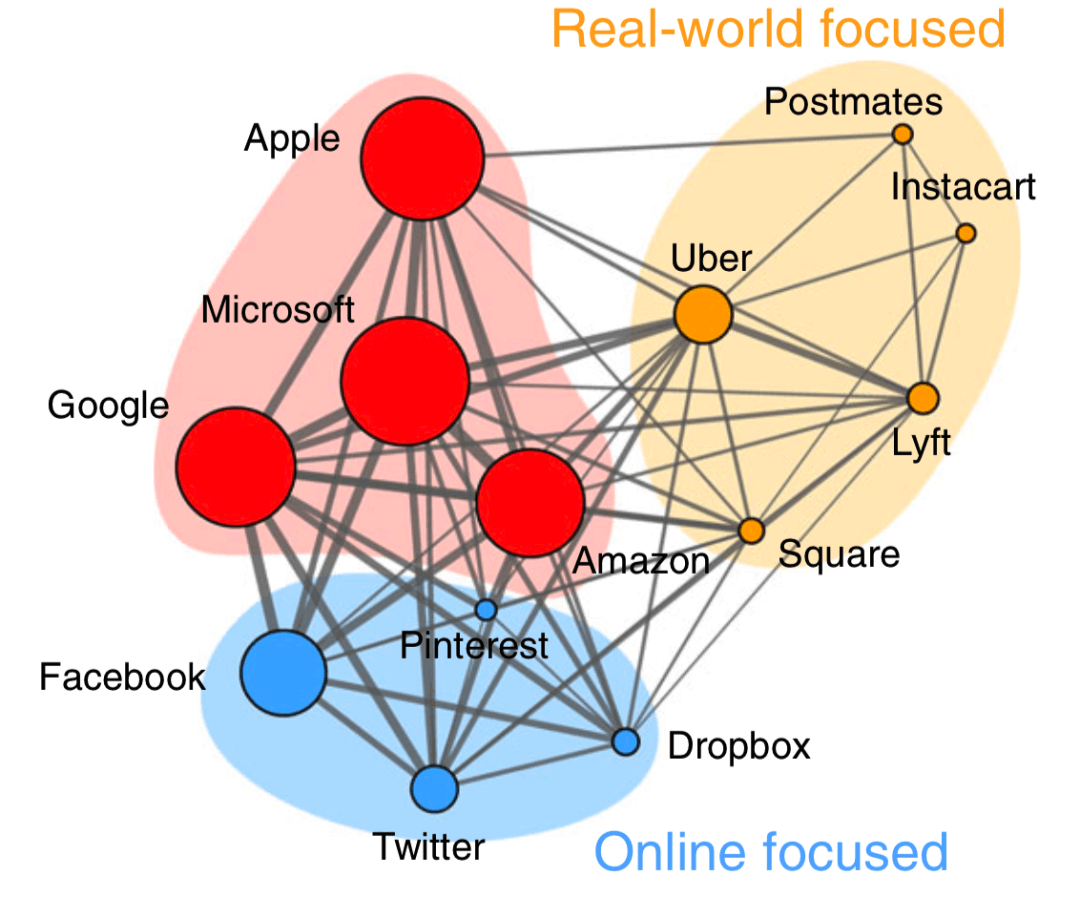

图4：运用模块度最大值算法检测出的社团。节点为公司，边为公司间职员的流动。蓝色为线上为主的公司、黄色为线下为主的公司、红色为线上线下兼顾的公司。

2、怎么表示一个随机图

一个好的社区一定是内部的连接要比随机连接情况下的连接更紧密。说到随机，那自然需要一个零模型(图模型)，这里选择的是配置模型(configuration model)，为了保证与原图有相同的度分布。类似与在介绍 motifs 时，运用的模型，不同的是，这里允许有重边(multi edge)的 multigraph。

四、Louvain 算法

louvain 算是目前市面上提到的和使用过的最常用的社区发现算法之一了，除此之外就是 infomap，这两种。原始论文为：《Fast unfolding of communities in large networks》。所以又被称为Fast unfolding算法。

模块度（Modularity）用来衡量一个社区的划分是否优良。一个好的划分结果其表现形式是：在社区内部的节点相似度较高，而在社区外部节点的相似度较低。模块度的定义由于当时研究的图类型的不同而一直发生变化，

模块度是评估一个社区网络划分好坏的度量方法，它的物理含义是社区内节点的连边数与随机情况下的边数之差，它的取值范围是 [−1/2,1)，其定义如下：

结论：模块度越大，挖掘的社区内部连接越紧密，效果越好。

对无权图：模块度社区内部边的度数减去社区内节点的总度数。
对于权重图：模块度也可以理解是社区内部边的权重减去所有与社区节点相连的边的权重和。
既然，模块度是评价社区结构好坏的指标。那么，自然可以通过最大化模块度来识别社区。这就是下面算法的思想。

1、不同密度社区对比

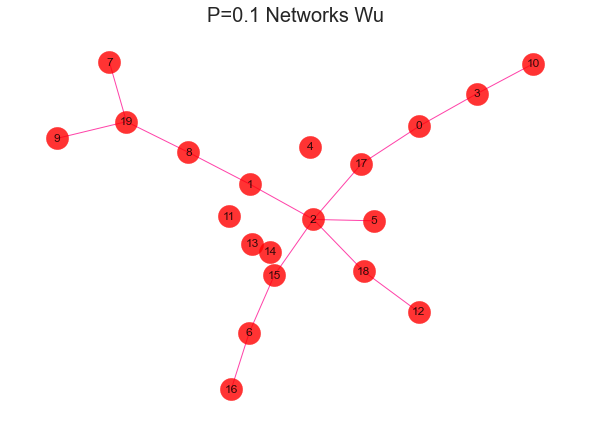
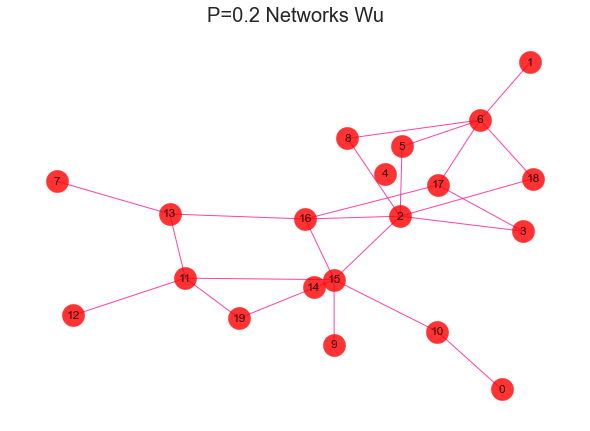
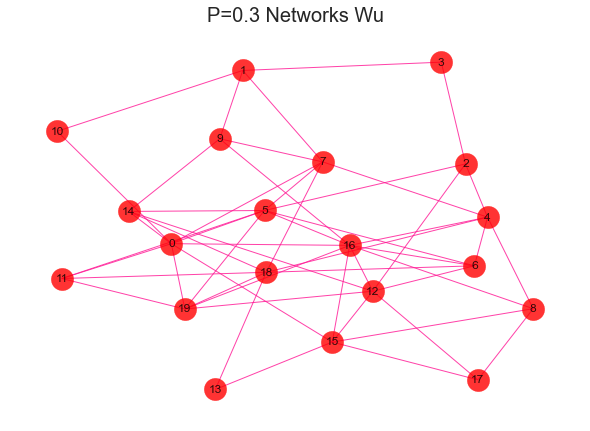
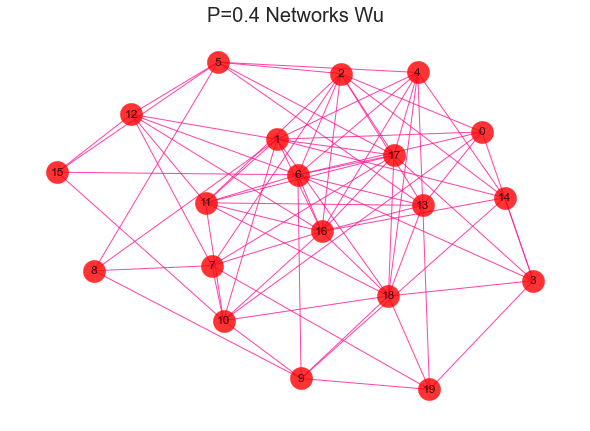
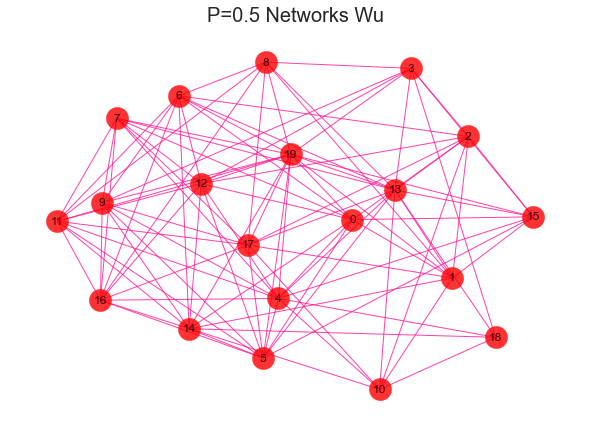
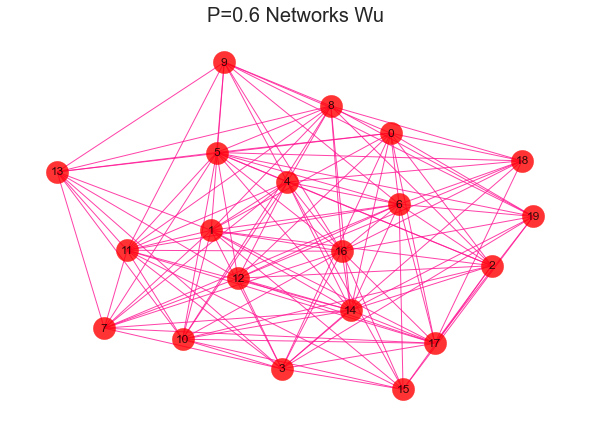
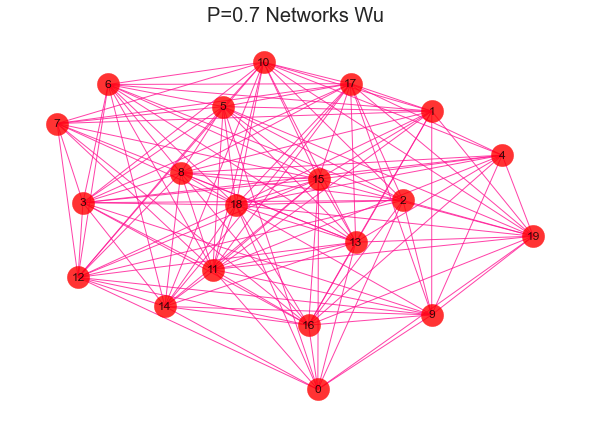
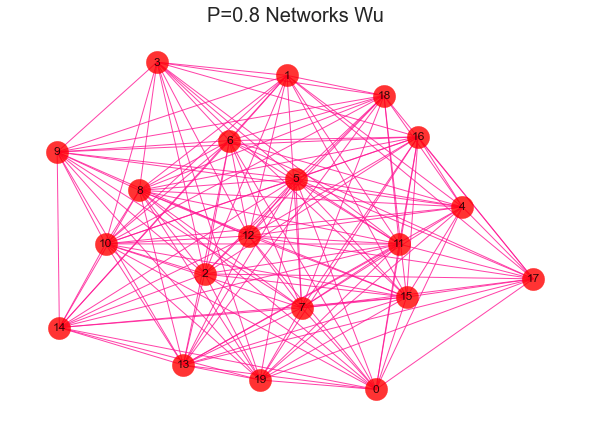
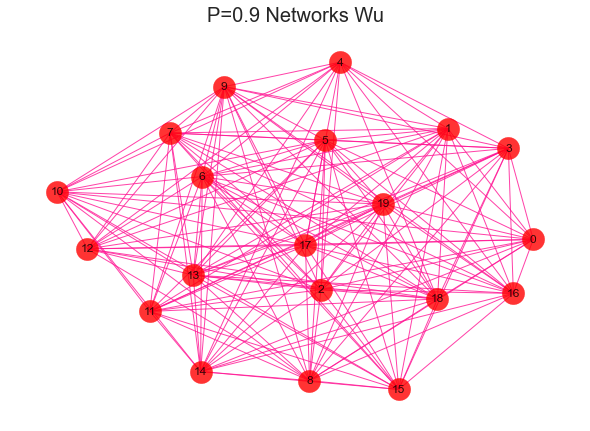
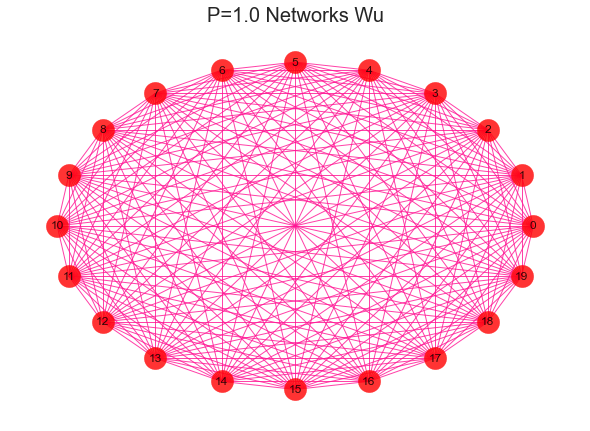
这个公式的含义一定要理解清楚才能体会到 louvain 背后的真谛，我们来直观的看看，不同紧密程度的社区长什么样子。

#导入建网络模型包，导入科学绘图包
import networkx as nx
import matplotlib.pyplot as plt 
'''
随机生成网络 用erdos_renyi_graph(n,p)方法生成一个含有n个节点、
以概率p连接的ER随机图，在本程序中以概率0.8连接20个节点中的每一对节点，完成图形。
'''
for i in range(1,11):
    rate = i/10   
    print(rate) 
    G  = nx.erdos_renyi_graph(20,rate)
    nx.draw(G,
            with_labels=True,
            pos=nx.kamada_kawai_layout(G),
            #width=edgewidth,
            node_size=500,
            alpha=0.8,
            node_color="r",
            edge_color="DeepPink"
            )
    text = 'P={rate} Networks Wu'.format(rate=rate)
    plt.title(text, fontsize = 20)
    plt.show()

2、社区发现效果评估-模块化指数Q

光说思路是没有意义的，在数学上应该如何定义社区发现效果的好坏呢？结论就是直接和随机模型比较就好啦！
你问我什么叫随机模型？简单来说就是图中节点和边数量不变，把节点之间连接关系随机打乱。那么根据这个思路，如果这个图一点都不像随机图，那么说明这个图存在一定的社区结构！
用方程可以这样表示（看不懂没关系，往下翻就对了）：

模块度是评估一个社区网络划分好坏的度量方法，它的物理含义是社区内节点的连边数与随机情况下的边数之差，它的取值范围是 [−1/2,1)，其定义如下：

Q的取值范围是[−1 , 1]，一般认为取值在0.3~0.7之间就认为有明显的社区结构出现了。这个公式的含义一定要理解清楚才能体会到 louvain 背后的真谛。

可以简单理解为，固定节点数，给定图的连接有多少条边，用同样多的节点，随机生成的图，有多少个边，相减，得到的差越大，说明给定图越紧密。
为了更好的理解这里举一个具体的例子：

3、社区发现算法-Louvain

在现实生活中，存在着各种各样的社会网络，比如人际关系网、交通网、金融网等，对这些网络进行社区发现具有极大的意义。
例如在社交网络中社区发现、基于好友关系为用户推荐商品或内容、社交网络中人物影响力的计算、信息在社交网络上的传播模型、虚假信息和机器人账号的识别、基于社交网络信息对股市、大选以及金融行业中的反欺诈预测等。时下，社交网络爆发，图数据库应用火爆，其中，Louvain（鲁汶）算法在图数据分析领域的众多算法中是比较复杂的，同时别具意义。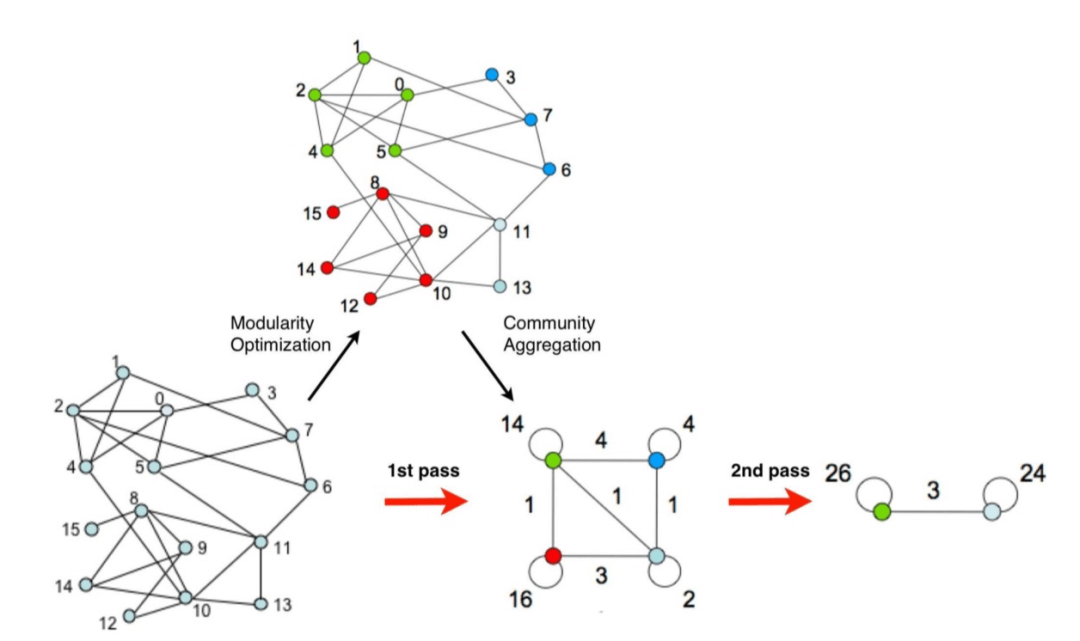

好家伙，到这里才算是引出了本文的正题。截至到本文发布，Louvain算法还是社区发现算法里的靓仔，与infomap算法共同成为调包侠们的最爱。

Louvain算法的思路也很简单，一句话：不择手段把图的模块化指数Q搞大。
事实上Louvain算法也就是个贪心算法，主要分为以下几步：

第一步，将图中每个节点都看作一个社区（没错就是一个节点的社区），尝试让某个节点加入邻居的社区，计算图的模块化指数增量ΔQ，并最终选择一个ΔQ最大的邻居社区加入，比如下图我们从编号为0的节点开始，经过第一步后有如下过程：

有些同学可能会问，每次都要重新计算全局的ΔQ也太麻烦了叭，当然我们有更简单的办法啦，这个时候我们只需要计算这个局部ΔQ就可以惹，那么这个局部ΔQ就可以表示为：

• ∑in是社区C内部连接权重之和
• ∑tot是社区C所有连接权重的和，包括社区与外部的链接；
• ki,in是节点i和社区C之间连接权重之和；
• Ki是与节点i相关的所有连接权重之和。

仔细想想确实还挺有道理，但是我懒，调包就完事儿了（手动狗头）

第二步，在第一步的基础上，把划分出来的社区当成一个超节点看待，如下图所示：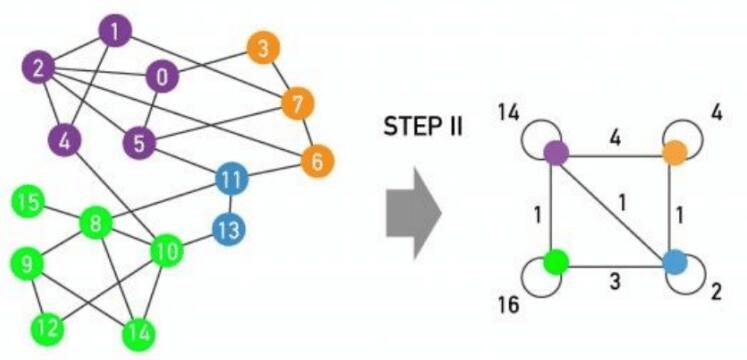

这里需要注意两点：

• 超节点对应的社区内部存在边，需要把它们的权重求和，并作为超节点自环的权重
• 超节点之间的社区存在边，需要把它们的权重求和，并作为超节点之间的边权重

第三步，如果算法已经达到了目标（比如最大的ΔQ小于某个值）那么算法结束，否则将超节点视为普通节点，并回到第一步。这里展示第二轮循环的结果：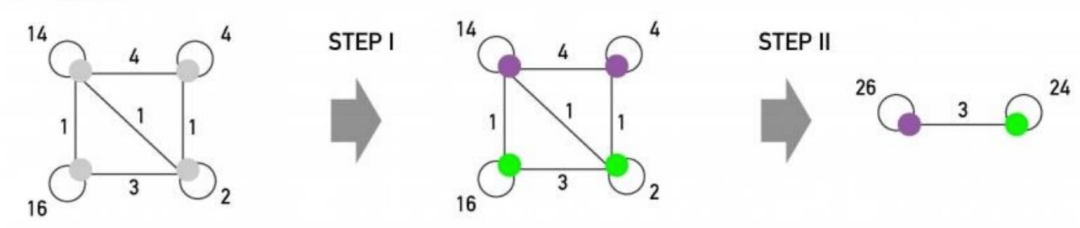

五、基本概念—权重度

Louvain（鲁汶）算法是基于模块度（modularity）计算的社区识别算法，是以最大化模块度为目标的一种对顶点进行聚类的迭代过程。该算法由比利时鲁汶大学的 Vincent D.Blondel 等人于 2008 年提出，因其能以较高的效率计算出令人满意的社区识别结果，而成为近年来最多被提及和使用的社区识别算法。主要用于社交网虚假账号识别、消费群体划分及商品推荐、银行卡伪冒和欺诈团伙识别、银行理财产品、保险产品推荐、企业集团及家族企业识别等领域。
Louvain（鲁汶）算法的基本概念包括：
1、权重度
2、社区压缩
3、模块度
4、模块度增
权重度是考虑了边上权重的度的计算。鲁汶算法在计算模块度时用到了节点权重度和社区权重度两个概念。

1、节点权重度

节点权重度是指与某个点有关（以该点为端点）的所有边的权重和，包括该点的邻边（连接至其它点）以及该点的自环边（连接至该点自身）。

图1：节点权重度
如图1所示，红色节点有三条邻边和一条自环边，因此该点的权重度为 1 + 0.5 + 3 + 1.5 = 6 （注意：自环的权重只被计算1次）。

2、社区权重度

社区权重度是指一个社区内所有节点的权重度的和。

图2：社区权重度
如图2所示:
红色节点的权重度为 1 + 0.5 + 3 + 1.5 = 6
绿色节点的权重度为 1 + 1.7 = 2.7
蓝色节点的权重度为 0.5 + 0.3 + 2 = 2.8
黄色节点的权重度为 3
因此 1 号社区的权重度为 6 + 2.7 + 2.8 + 3 = 14.5

3、社区内部权重度

社区内部权重度是指在计算一个社区的权重度时，仅考虑两个端点均在该社区内的边；或者说，从该社区的权重度中去掉该社区和其它社区之间的边的权重，即为该社区的内部权重度。
如上图所示，Ⅰ号社区和其它两个社区之间共有三条边，权重分别为 1.7、0.3 和 2，因此Ⅰ号社区的内部权重度为 14.5 - 1.7 - 0.3 - 2 = 10.5

注意，社区内部权重度并不是两个端点均在社区内的边的权重和，而是这些边当中的非自环边的权重和的二倍再加上自环边的权重和。原因是非自环边的两个端点会令该边被计算两次。换句话说，社区内部除了自环类型的边的权重只被计算一次，其它边会被计算两次——因为每个边会连接2个端点，按照社区内部权重度的定义，边的权重需要x2。
用上一张图进行验证，Ⅰ号社区的内部权重度可以计算为 (1 + 0.5 + 3) * 2 + 1.5 = 10.5

4、全图权重度

全图权重度是指图中所有节点的权重度的和。如果将全图划分为多个社区，由于图中每个点属于并且仅属于一个社区，全图权重度也等于这些社区的权重度的和。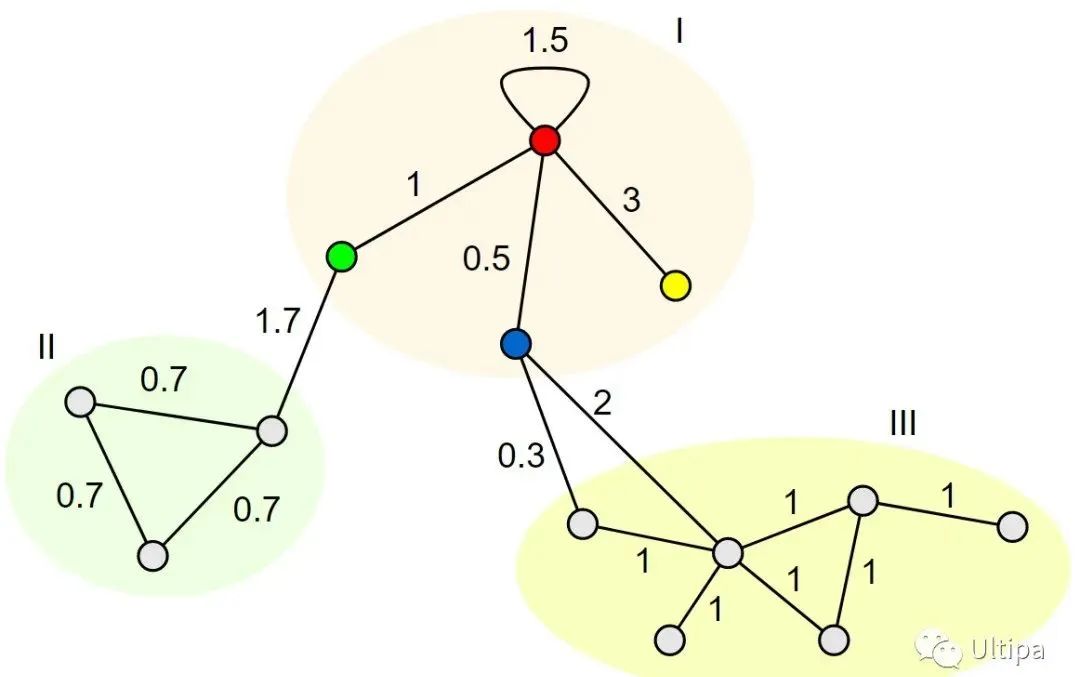

图3：全图权重度
如图3所示，Ⅰ号社区的权重度为 14.5，Ⅱ号社区的权重度为 0.7 3 2 + 1.7 = 5.9，Ⅲ号社区的权重度为 1 6 2 + 0.3 + 2 = 14.3，全图的权重度为 14.5 + 5.9 + 14.3 = 34.7

如果将全图看成一个社区，那么全图权重度也可以理解为该社区的内部权重度。还用上图进行验证，全图权重度为 (1 + 0.5 + 3 + 1.7 + 0.7 3 + 0.3 + 2 + 1 6) * 2 + 1.5 = 34.7

以上两种计算方法的结果可以相互印证，并且应该是一致的。

六、基本概念—社区压缩

时下，社交网络爆发，图数据库应用火爆，其中，Louvain（鲁汶）算法在图数据分析领域的众多算法中是比较复杂的，同时别具意义。在上节的“文库”中，我们详细解读了权重度，本节将具体对社区压缩进行科普。做好准备，干货来了！

1、什么是社区压缩？

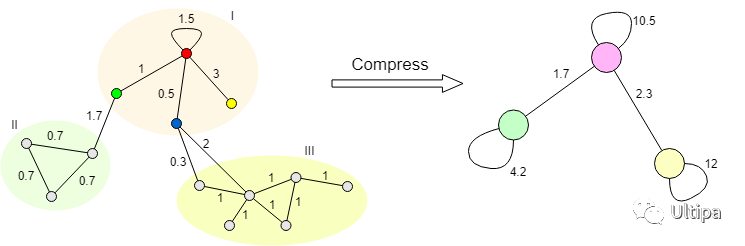
社区压缩是将每个社区内的所有节点用一个聚合点来表示，该社区的内部权重度即为此聚合点的自环边的权重，每两个社区间的边的权重和即为相应两个聚合点之间的边的权重。

如动图所示，对I、II、III三个社区进行压缩，I号社区压缩后的自环边的权重为该社区的内部权重，即 10.5；II 号社区压缩后自环边的权重为 0.7 3 2 = 4.2，III 号社区压缩后自环边的权重为 1 6 2 = 12。同时，I 号与 II号社区之间的边压缩后权重为 1.7，与 III 号社区之间的边压缩后权重为 0.3 + 2 = 2.3。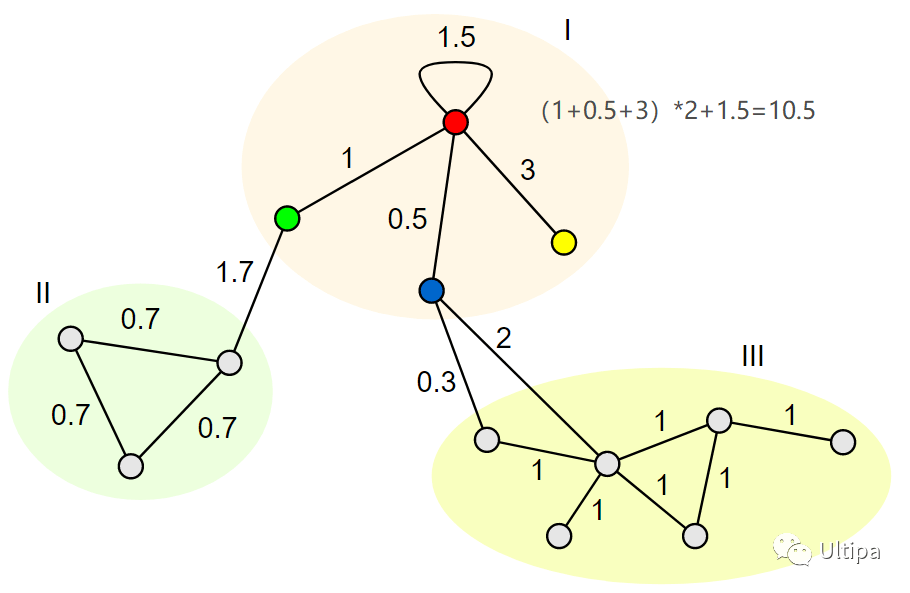

插播一段，看上图。注意呀，以I号社区为例，它的权重度等于10.5。除了自环边，其中红绿、红蓝和红黄的点边，都需要分别计算2次哦。

综上，经过倒推计算可知，压缩后的全图权重度为 10.5 + 4.2 + 12 + (1.7 + 2.3) * 2 = 34.7，与压缩前相同。

压缩前和压缩后的结果，是相等的呀！

2、为什么要进行社区压缩？

在鲁汶算法中，使用了大量的社区压缩。那为什么要进行压缩呢？它的作用是什么呢？究其本质来看，进行社区压缩有两方面的好处：
一是，让计算效率变高。进行社区压缩，在不改变局部权重度及全图权重度的前提下，通过最大限度减少图的点、边数量来提高后续（迭代）的计算速度；

二是，实现层级化的社区划分。社区内的点在压缩后将作为一个整体进行模块度优化的计算，不再拆分，从而实现了层级化（迭代化）的社区划分效果。

七、Louvain算法结果处理

细心的同学肯定发现了，经过Louvain算法计算后的社区，是一个多层次的结构，通常来说它会是这样的：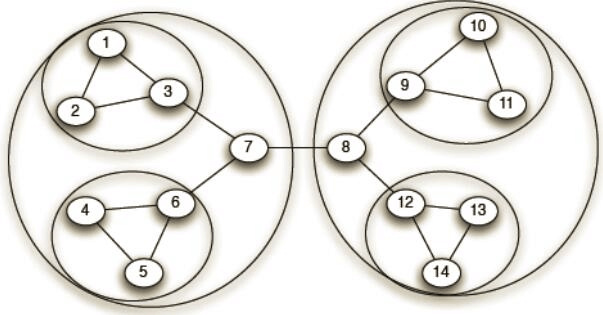

那么选取哪个层次的社区结构也是比较头疼的过程呢。这里我建议可以将手肘法作为辅助工具，当模块化指数Q或社区数量随着迭代次数增加出现明显拐点的时候，选取对应层次的社区结构就比较合理啦，比如下面这样的：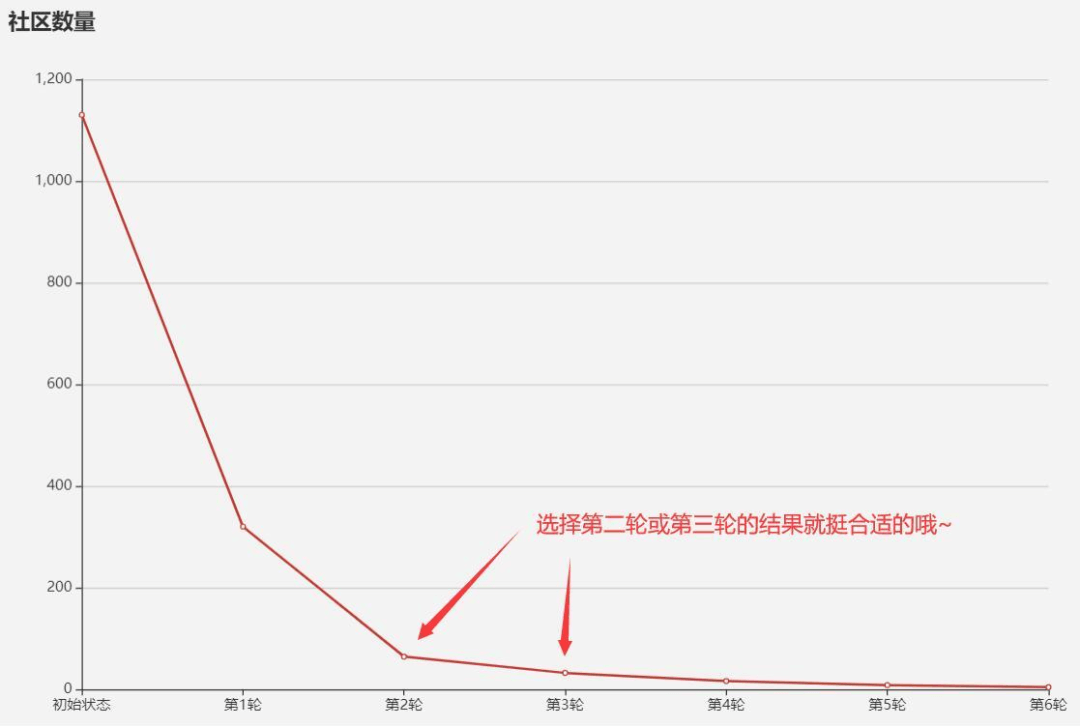

八、Louvain算法应用

很多人在调用community.best_partiton()方法时，总是报错：AttributeError: ‘module’ object has no attribute ‘best_partition，一直使用失败，许多网络上代码直接调用 import community， 就以为这个包叫community，实际上，这个包叫python-louvain。包的地址为：https://github.com/taynaud/python-louvain

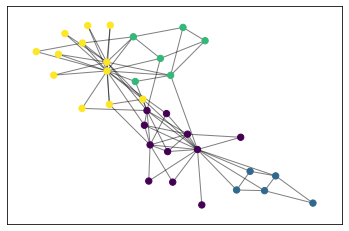
#安装的方法为：pip install python-louvain
#调用的方法为from community import community_louvain

如果遇到问题，可以按下面的方法进行安装

'''
不要单独安装networkx和community ，会导致Graph没有best_parition属性。
安装与networkx 2.x 版本对应的python-louvain(它内部包含了community)
'''
# pip install -U git+https://github.com/taynaud/python-louvain.git@networkx2
# 安装 networkx,理论上应该默认安装最新版版的 2.4
# pip install networkx
# 调用并测试分群的结果                                                                                       
from community import community_louvain
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import networkx as nx
# load the karate club graph
G = nx.karate_club_graph()
# 对图数据进行社群划分
partition = community_louvain.best_partition(G)
# 查看分组情况
print(partition)
# {0: 0, 1: 0, 2: 0, 3: 0, 4: 1, 5: 1, 6: 1, 7: 0, 8: 3, 9: 3, 10: 1, 
#  11: 0, 12: 0, 13: 0, 14: 3, 15: 3, 16: 1, 17: 0, 18: 3, 19: 0, 
#  20: 3, 21: 0, 22: 3, 23: 2, 24: 2, 25: 2, 26: 3, 27: 2, 28: 2, 
#  29: 3, 30: 3, 31: 2, 32: 3, 33: 3
# }
#在实际应用的时候，我们一般转换成DataFrame
import pandas as pd
pd.DataFrame({'Id':partition.keys(),'Group':partition.values()})
#     Id  Group
# 0    0      0
# 1    1      0
# 2    2      0
# 3    3      0
# 4    4      1
# 5    5      1
# 6    6      1
# 7    7      0
# 8    8      3
# 9    9      3
# draw the graph
pos = nx.spring_layout(G)
# color the nodes according to their partition
cmap = cm.get_cmap('viridis', max(partition.values()) + 1)
nx.draw_networkx_nodes(G, 
                       pos, 
                       partition.keys(), 
                       node_size=40,
                       cmap=cmap, 
                       node_color=list(partition.values())
                      )
nx.draw_networkx_edges(G, pos, alpha=0.5)
# AttributeError: module 'matplotlib.cbook' has no attribute 'iterable'
# pip install --upgrade networkx  这个代码修复  Successfully installed networkx-3.0
plt.show()