来源：https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650187831&idx=1&sn=6d2c49c181aa173df08d6e70ad5f5ca2&chksm=88238ff3bf5406e5d70b96c854ae77ae1e00a3099bb1269bd315b8d4b1114ec0a03d746643c8&scene=21#wechat_redirect

风控策略同学在挖掘有效的风控规则的时候，经常需要基于业务经验，将那几个特征进行组合形成风控策略，会导致在特征组合的时候浪费大量的时间，我们有没有什么方法，替代人工的分析，直接得出策略组合呢，决策树就是其中的一个选择，可以实现自动化的挖掘大批量的策略组合。
在众多的算法中，决策树整体分类准确率不高，但是部分叶子节点的准确率却可以很高，因此我们可以提取决策树的叶子规则，并筛选准确率比较高的叶子节点，作为风控策略挖掘手段，并进行策略推荐，替代人工或者辅助人工，大大提高策略发现的效率于效果。

数据下载：https://pan.baidu.com/s/14YTXEhoUf_4HYKtZKIhayg?dp-logid=70888500703050440002#/home/%2F/%2F

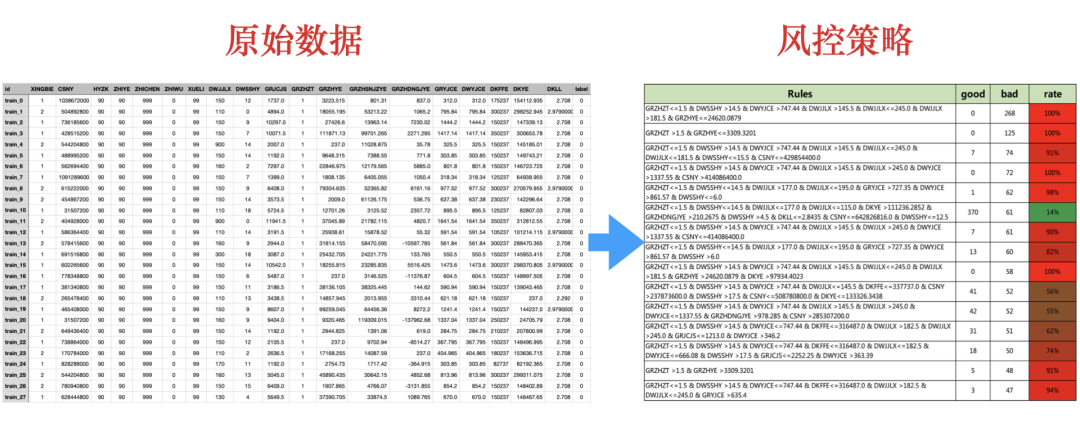
*决策树三种可视化展示形态 - 图1
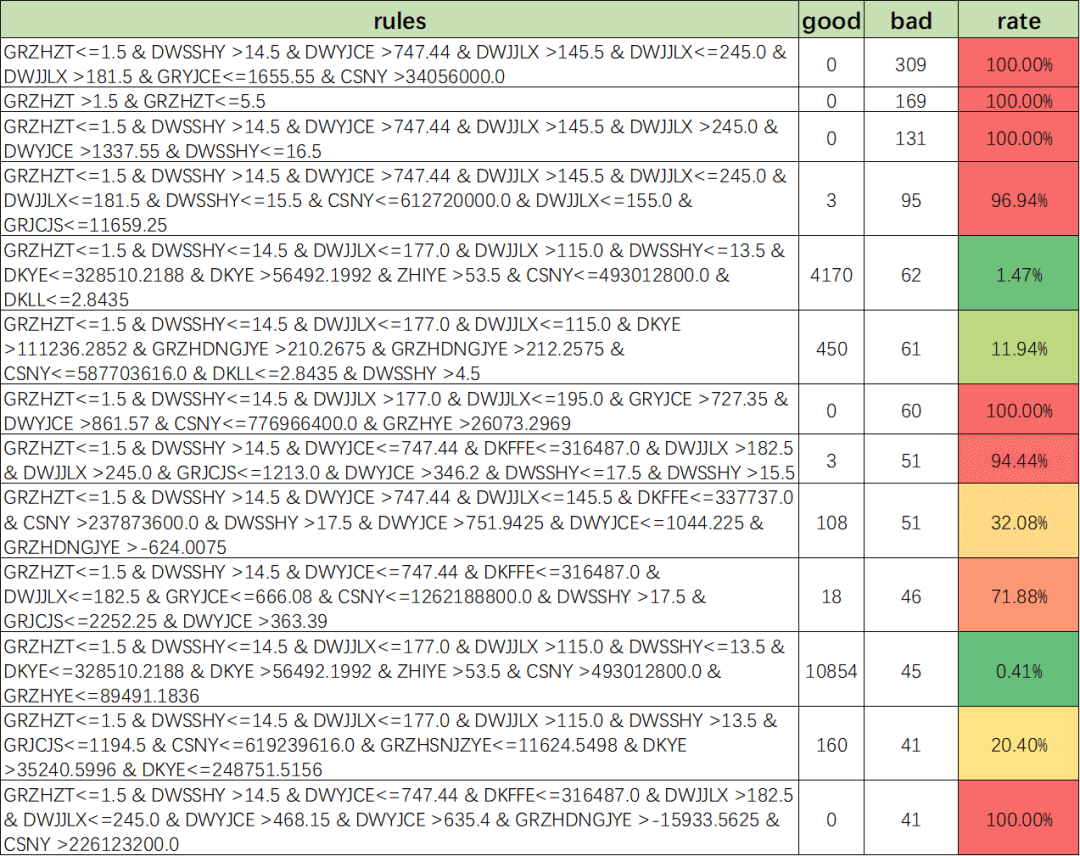
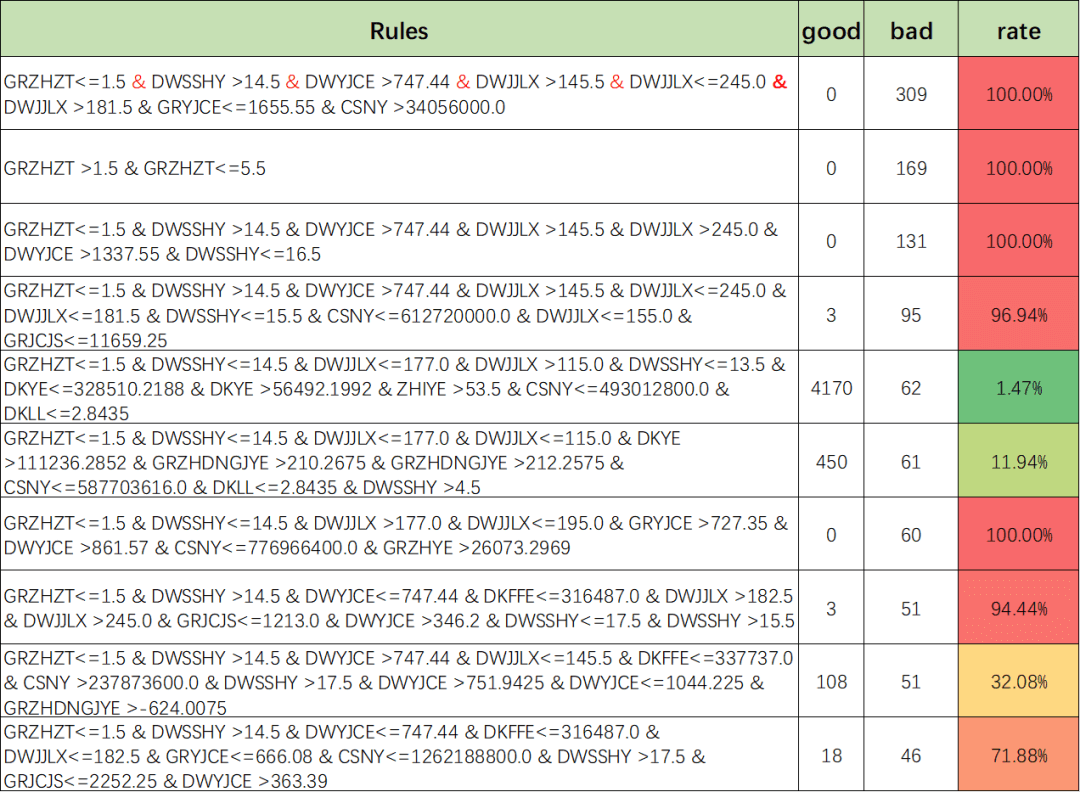
策略节选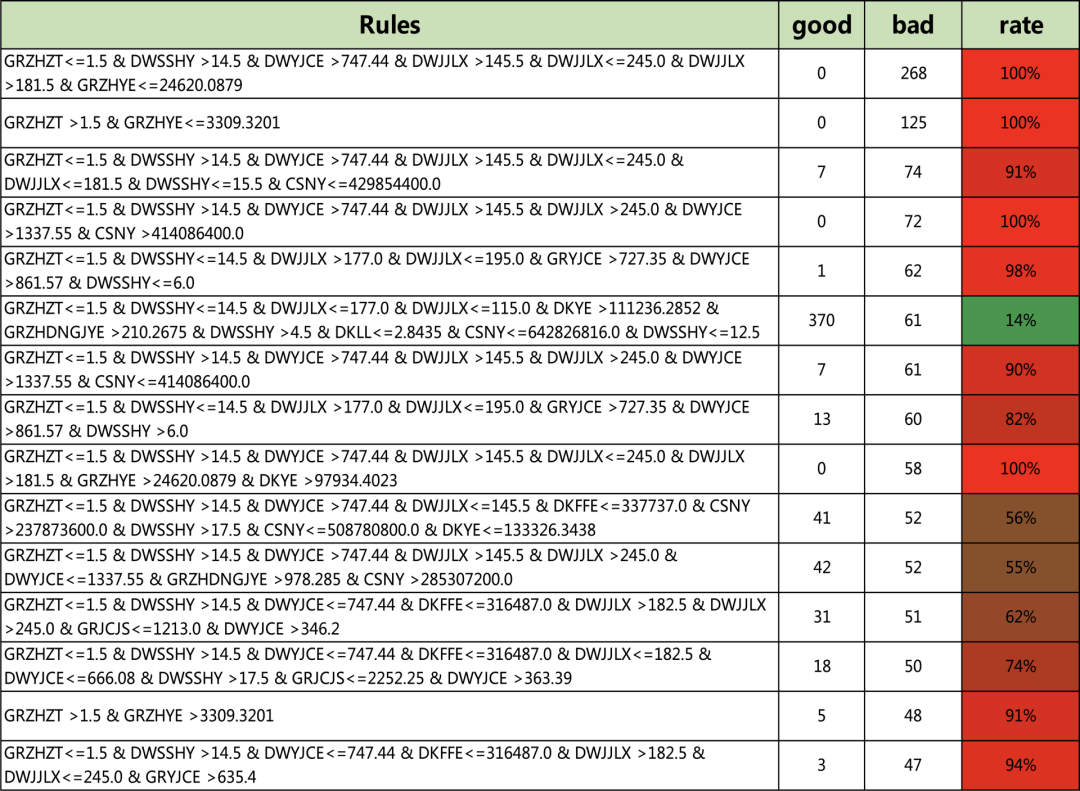
*决策树三种可视化展示形态 - 图2

代码：

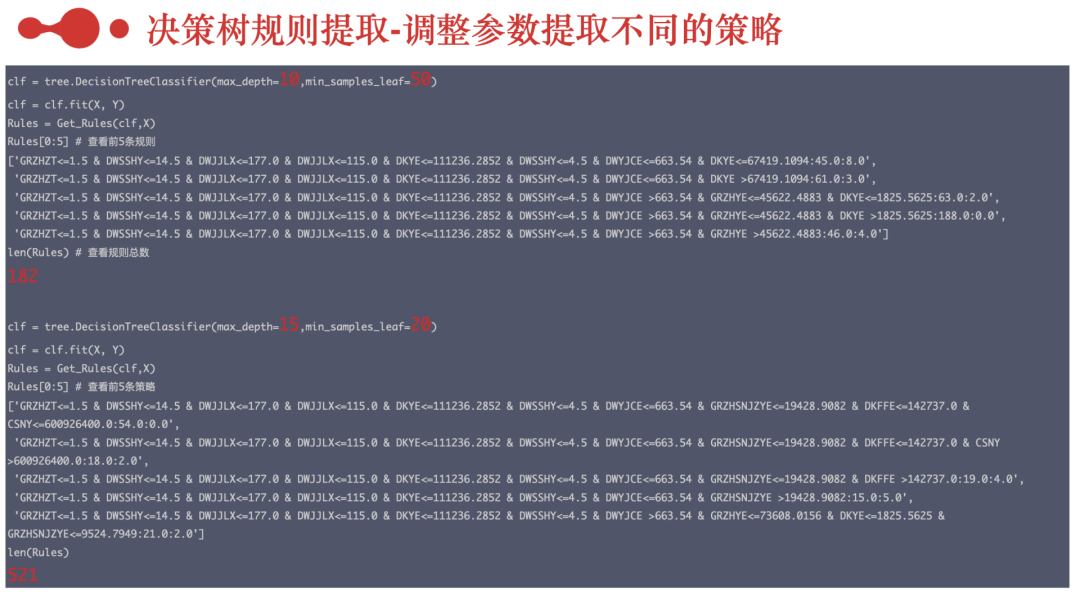
  1. # -*- coding: utf-8 -*-
  2. """
  3. Created on Wed Mar 29 08:55:46 2023
  5. @author: yingtao.xiang
  6. """
  8. #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
  9. # 一、数据读取 #
  10. import pandas as pd
  11. import numpy  as np
  12. pd.set_option('display.max_columns', None)#显示所有的列
  13. path  = '/Users\yingtao.xiang\Downloads/train.csv'
  14. train = pd.read_csv(path).fillna(-1)
  15. train.columns
  16. # Index(['id', 'XINGBIE', 'CSNY', 'HYZK', 'ZHIYE', 'ZHICHEN', 'ZHIWU', 'XUELI',
  17. #        'DWJJLX', 'DWSSHY', 'GRJCJS', 'GRZHZT', 'GRZHYE', 'GRZHSNJZYE',
  18. #        'GRZHDNGJYE', 'GRYJCE', 'DWYJCE', 'DKFFE', 'DKYE', 'DKLL', 'label'],
  19. #       dtype='object')
  23. train.head()#查看前面的数据
  24. #  id  XINGBIE        CSNY  HYZK  ZHIYE  ZHICHEN  ZHIWU  XUELI  DWJJLX  \
  25. # 0  train_0        1  1038672000    90     90      999      0     99     150   
  26. # 1  train_1        2   504892800    90     90      999      0     99     110   
  27. # 2  train_2        1   736185600    90     90      999      0     99     150   
  28. # 3  train_3        1   428515200    90     90      999      0     99     150   
  29. # 4  train_4        2   544204800    90     90      999      0     99     900   
  31. #    DWSSHY   GRJCJS  GRZHZT      GRZHYE  GRZHSNJZYE  GRZHDNGJYE   GRYJCE  \
  32. # 0      12   1737.0       1    3223.515     801.310     837.000   312.00   
  33. # 1       0   4894.0       1   18055.195   53213.220    1065.200   795.84   
  34. # 2       9  10297.0       1   27426.600   13963.140    7230.020  1444.20   
  35. # 3       7  10071.5       1  111871.130   99701.265    2271.295  1417.14   
  36. # 4      14   2007.0       1     237.000   11028.875      35.780   325.50   
  38. #     DWYJCE   DKFFE        DKYE   DKLL  label  
  39. # 0   312.00  175237  154112.935  2.708      0  
  40. # 1   795.84  300237  298252.945  2.979      0  
  41. # 2  1444.20  150237  147339.130  2.708      0  
  42. # 3  1417.14  350237  300653.780  2.708      0  
  43. # 4   325.50  150237  145185.010  2.708      0  
  45. #构建训练集
  46. X = train.loc[:,'XINGBIE':'DKLL']
  47. Y = train['label']
  51. from sklearn import tree
  52. clf = tree.DecisionTreeClassifier(
  53.      max_depth=3,
  54.      min_samples_leaf=50
  55.      )
  56. clf = clf.fit(X, Y)
  57. #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
  61. #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
  62. # 二、决策树的可视化 #
  63. # 1、plot_tree（太丑，不推荐）
  65. #包里自带的，有点丑
  66. tree.plot_tree(clf)
  67. plt.show()
  70. # 2、graphviz对决策树进行可视化
  71. import graphviz 
  72. dot_data = tree.export_graphviz(
  73.                      clf, 
  74.                      out_file=None, 
  75.                      feature_names=X.columns,  
  76.                      class_names=['good','bad'],  
  77.                      filled=True, rounded=True,  
  78.                      special_characters=True)  
  79. graph = graphviz.Source(dot_data)  
  80. graph
  82. # 3、dtreeviz对决策树进行可视化
  84. # cannot import name 'dtreeviz' from 'dtreeviz.trees'
  86. # 这里代码 不对 现在不用这个dtreeviz.trees
  88. # from dtreeviz.trees import dtreeviz
  89. # testX = X.iloc[77,:]
  90. # viz = dtreeviz(clf,X,Y,
  91. #         feature_names=np.array(X.columns),
  92. #         # class_names=['good','bad'],
  93. #         class_names={0:'good',1:'bad'},
  94. #         X = testX)              
  95. # viz.view()
  98. # 最新代码 是用  dtreeviz.model
  99. import dtreeviz
  102. # viz_model = dtreeviz.model(clf,
  103. #                            X_train=X, y_train=y,
  104. #                            feature_names=iris.feature_names,
  105. #                            target_name='iris',
  106. #                            class_names=iris.target_names)
  108. # v = viz_model.view()     # render as SVG into internal object 
  109. # v.show()                 # pop up window
  110. # v.save("/tmp/iris.svg")  # optionally save as svg
  112. testX = X.iloc[77,:]
  113. # feature_names 要list
  114. viz = dtreeviz.model(clf,
  115.                     X_train=X, y_train=Y,
  116.                     feature_names=X.columns,
  117.                     class_names=['good','bad']
  118.                     # feature_names=np.array(X.columns),
  119.                     # class_names=['good','bad'],
  120.                     # class_names={0:'good',1:'bad'}
  121.                     )              
  122. v=viz.view()
  123. v.show()
  126. # def model(model,
  127. #           X_train,
  128. #           y_train,
  129. #           tree_index: int = None,
  130. #           feature_names: List[str] = None,
  131. #           target_name: str = None,
  132. #           class_names: (List[str], Mapping[int, str]) = None)
  135. # 我们把树的深度再加深到5看看，树更复杂了
  136. from sklearn import tree
  137. clf = tree.DecisionTreeClassifier(
  138.      max_depth=5,
  139.      min_samples_leaf=50
  140.      )
  141. clf = clf.fit(X, Y)
  144. testX = X.iloc[77,:]
  145. viz = dtreeviz.model(clf,
  146.                     X_train=X, y_train=Y,
  147.                     feature_names=X.columns,
  148.                     # feature_names=np.array(X.columns),
  149.                     # class_names=['good','bad'],
  150.                     class_names={0:'good',1:'bad'}
  151.                     )              
  152. v=viz.view()
  153. v.show()
  155. # from dtreeviz import trees
  156. # from dtreeviz.models.sklearn_decision_trees import ShadowSKDTree
  157. # from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
  158. # random_state=1234
  160. # dataset=X
  163. # tree_classifier = DecisionTreeClassifier(max_depth=4, random_state=random_state)
  164. # tree_classifier.fit(X, Y)
  165. # sk_dtree = ShadowSKDTree(tree_classifier, X, Y, X.columns, 'label', [0, 1])
  167. # trees.dtreeviz(tree_classifier, X, Y, X.columns, 'label', class_names=[0, 1])
  169. # trees.dtreeviz(sk_dtree, fancy=False)
  172. #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
  175. #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
  176. # 四、决策规则提取 #
  177. # 1、决策树的生成的结构探索
  179. from sklearn.datasets import load_iris
  180. from sklearn import tree
  181. iris = load_iris()
  182. clf = tree.DecisionTreeClassifier()
  183. clf = clf.fit(iris.data, iris.target)
  184. clf.classes_
  185. [x for x in dir(clf) if not x.startswith('_')]
  188. dir(clf.tree_)
  189. # ['apply','capacity', 'children_left','children_right',
  190. #  'compute_feature_importances','compute_partial_dependence',
  191. #  'decision_path','feature',
  192. #  'impurity','max_depth',
  193. #  'max_n_classes','n_classes',
  194. #  'n_features','n_leaves',
  195. #  'n_node_samples','n_outputs','node_count',
  196. #  'predict','threshold',
  197. #  'value', 'weighted_n_node_samples']
  200. # 2、老方法提取决策树规则
  202. import pandas as pd
  203. import numpy  as np
  204. pd.set_option('display.max_columns', None)#显示所有的列
  205. path  = '/Users\yingtao.xiang\Downloads/train.csv'
  206. train = pd.read_csv(path).fillna(-1)
  207. train.columns
  210. X = train.loc[:,'XINGBIE':'DKLL']
  211. Y = train['label']
  213. from sklearn import tree
  214. clf = tree.DecisionTreeClassifier(
  215.      max_depth=3,
  216.      min_samples_leaf=50
  217.      )
  218. clf = clf.fit(X, Y)
  220. from sklearn.tree import _tree
  221. def tree_to_code(tree, feature_names):
  222.     tree_ = tree.tree_
  223.     feature_name = [
  224.         feature_names[i] if i != _tree.TREE_UNDEFINED else "undefined!"
  225.         for i in tree_.feature
  226.     ]
  227.     print ("def tree({}):".format(", ".join(feature_names)))
  229.     def recurse(node, depth):
  230.         indent = "  " * depth
  231.         if tree_.feature[node] != _tree.TREE_UNDEFINED:
  232.             name = feature_name[node]
  233.             threshold = tree_.threshold[node]
  234.             print("{}if {} <= {}:".format(indent, name, threshold))
  235.             recurse(tree_.children_left[node], depth + 1)
  236.             print("{}else:  # if {} > {}".format(indent, name, threshold))
  237.             recurse(tree_.children_right[node], depth + 1)
  238.         else:
  239.             print("{}return {}".format(indent, tree_.value[node]))
  241.     recurse(0, 1)
  243. tree_to_code(clf,X.columns)
  244. # def tree(XINGBIE, CSNY, HYZK, ZHIYE, ZHICHEN, ZHIWU, XUELI, DWJJLX, DWSSHY, GRJCJS, GRZHZT, GRZHYE, GRZHSNJZYE, GRZHDNGJYE, GRYJCE, DWYJCE, DKFFE, DKYE, DKLL):
  245. #   if GRZHZT <= 1.5:
  246. #     if DWSSHY <= 14.5:
  247. #       if DWJJLX <= 177.0:
  248. #         return [[24563.   524.]]
  249. #       else:  # if DWJJLX > 177.0
  250. #         return [[4969.  443.]]
  251. #     else:  # if DWSSHY > 14.5
  252. #       if DWYJCE <= 747.4400024414062:
  253. #         return [[5309.  482.]]
  254. #       else:  # if DWYJCE > 747.4400024414062
  255. #         return [[2397. 1135.]]
  256. #   else:  # if GRZHZT > 1.5
  257. #     if GRZHYE <= 3309.320068359375:
  258. #       return [[  0. 125.]]
  259. #     else:  # if GRZHYE > 3309.320068359375
  260. #       return [[ 5. 48.]]
  263. # 新方法提取决策树规则
  264. def Get_Rules(clf,X):
  265.     n_nodes = clf.tree_.node_count
  266.     children_left = clf.tree_.children_left
  267.     children_right = clf.tree_.children_right
  268.     feature = clf.tree_.feature
  269.     threshold = clf.tree_.threshold
  270.     value = clf.tree_.value
  272.     node_depth = np.zeros(shape=n_nodes, dtype=np.int64)
  273.     is_leaves  = np.zeros(shape=n_nodes, dtype=bool)
  274.     stack = [(0, 0)]
  276.     while len(stack) > 0:
  278.         node_id, depth = stack.pop()
  279.         node_depth[node_id] = depth
  281.         is_split_node = children_left[node_id] != children_right[node_id]
  283.         if is_split_node:
  284.             stack.append((children_left[node_id],  depth+1))
  285.             stack.append((children_right[node_id], depth+1))
  286.         else:
  287.             is_leaves[node_id] = True  
  288.     feature_name = [
  289.             X.columns[i] if i != _tree.TREE_UNDEFINED else "undefined!"
  290.             for i in clf.tree_.feature]
  292.     ways  = []
  293.     depth = []
  294.     feat = []
  295.     nodes = []
  296.     rules = []
  297.     for i in range(n_nodes):   
  298.         if  is_leaves[i]: 
  299.             while depth[-1] >= node_depth[i]:
  300.                 depth.pop()
  301.                 ways.pop()    
  302.                 feat.pop()
  303.                 nodes.pop()
  304.             if children_left[i-1]==i:#当前节点是上一个节点的左节点，则是小于
  305.                 a='{f}<={th}'.format(f=feat[-1],th=round(threshold[nodes[-1]],4))
  306.                 ways[-1]=a              
  307.                 last =' & '.join(ways)+':'+str(value[i][0][0])+':'+str(value[i][0][1])
  308.                 rules.append(last)
  309.             else:
  310.                 a='{f}>{th}'.format(f=feat[-1],th=round(threshold[nodes[-1]],4))
  311.                 ways[-1]=a
  312.                 last = ' & '.join(ways)+':'+str(value[i][0][0])+':'+str(value[i][0][1])
  313.                 rules.append(last)
  315.         else: #不是叶子节点 入栈
  316.             if i==0:
  317.                 ways.append(round(threshold[i],4))
  318.                 depth.append(node_depth[i])
  319.                 feat.append(feature_name[i])
  320.                 nodes.append(i)             
  321.             else: 
  322.                 while depth[-1] >= node_depth[i]:
  323.                     depth.pop()
  324.                     ways.pop()
  325.                     feat.pop()
  326.                     nodes.pop()
  327.                 if i==children_left[nodes[-1]]:
  328.                     w='{f}<={th}'.format(f=feat[-1],th=round(threshold[nodes[-1]],4))
  329.                 else:
  330.                     w='{f}>{th}'.format(f=feat[-1],th=round(threshold[nodes[-1]],4))              
  331.                 ways[-1] = w  
  332.                 ways.append(round(threshold[i],4))
  333.                 depth.append(node_depth[i]) 
  334.                 feat.append(feature_name[i])
  335.                 nodes.append(i)
  336.     return rules
  338. # 利用函数对规则进行提取
  339. #训练一个决策树，对规则进行提取
  340. clf = tree.DecisionTreeClassifier(max_depth=10,
  341. min_samples_leaf=50)
  342. clf = clf.fit(X, Y)
  343. Rules = Get_Rules(clf,X)
  345. Rules[0:5] # 查看前5条规则
  346. # ['GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE<=663.54 & DKYE<=67419.1094:45.0:8.0',
  347. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE<=663.54 & DKYE >67419.1094:61.0:3.0',
  348. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE >663.54 & GRZHYE<=45622.4883 & DKYE<=1825.5625:63.0:2.0',
  349. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE >663.54 & GRZHYE<=45622.4883 & DKYE >1825.5625:188.0:0.0',
  350. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE >663.54 & GRZHYE >45622.4883:46.0:4.0']
  351. len(Rules) # 查看规则总数
  352. # 182
  354. # 提高树的深度再看看，max_depth=15，可以看到规则数从182变成了521条，规模更大
  356. clf = tree.DecisionTreeClassifier(max_depth=15,min_samples_leaf=20)
  357. clf = clf.fit(X, Y)
  358. Rules = Get_Rules(clf,X)
  359. Rules[0:5]
  360. # ['GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE<=663.54 & GRZHSNJZYE<=19428.9082 & DKFFE<=142737.0 & CSNY<=600926400.0:54.0:0.0',
  361. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE<=663.54 & GRZHSNJZYE<=19428.9082 & DKFFE<=142737.0 & CSNY >600926400.0:18.0:2.0',
  362. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE<=663.54 & GRZHSNJZYE<=19428.9082 & DKFFE >142737.0:19.0:4.0',
  363. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE<=663.54 & GRZHSNJZYE >19428.9082:15.0:5.0',
  364. #  'GRZHZT<=1.5 & DWSSHY<=14.5 & DWJJLX<=177.0 & DWJJLX<=115.0 & DKYE<=111236.2852 & DWSSHY<=4.5 & DWYJCE >663.54 & GRZHYE<=73608.0156 & DKYE<=1825.5625 & GRZHSNJZYE<=9524.7949:21.0:2.0']
  365. len(Rules)
  366. # 521
  368. #可以遍历所有的规则
  369. for i in Rules:
  370.     print(i)
  372. pd.DataFrame(Rules).to_excel('rules.xlsx',index=False)
  373. #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#

一、数据说明及读取

1、数据集信息

数据从真实场景和实际应用出发，利用个人的基本身份信息、个人的住房公积金缴存和贷款等数据信息，来建立准确的风险控制模型，来预测用户是否会逾期还款。一共提供了40000带标签训练集样本，数据仅有一张表，一共有19个基本特征，且均不包含任何缺失值。

2、数据属性信息

标签：label是否逾期（是 = 1，否 = 0）。
特征：包含以下19个变量，名称和含义如下。

序号 字段名 类型 说明
1 id String 主键
2 XINGBIE int 性别
3 CSNY int 出生年月
4 HYZK int 婚姻状况
5 ZHIYE int 职业
6 ZHICHEN int 职称
7 ZHIWU int 职务
8 XUELI int 学历
9 DWJJLX int 单位经济类型
10 DWSSHY int 单位所属行业
11 GRJCJS float 个人缴存基数
12 GRZHZT int 个人账户状态
13 GRZHYE float 个人账户余额
14 GRZHSNJZYE float 个人账户上年结转余额
15 GRZHDNGJYE float 个人账户当年归集余额
16 GRYICE float 个人月缴存额
17 DWYICE float 单位月缴存额
18 DKFFE int 贷款发放额
19 DKYE float 贷款余额
20 DKLL float 贷款利率
21 label int 是否逾期 (0代表没逾期1代表逾期)

3、读取数据

二、构建决策树

三、决策树的可视化

决策树可视化的方案比较多，都写出来给对比看看，推荐第二种和第三种。对决策树进行可视化，是非常有必要的，能够帮助我们自己充分理解决策树的生成过程，如果是风控，也有利于咱们给业务部门解释数据和结果。

1、plot_tree（太丑，不推荐）

*决策树三种可视化展示形态 - 图3

2、graphviz对决策树进行可视化

如果搜索“可视化决策树”，很快便能找到由scikit提供的基于Python语言的解决方案：sklearn.tree.export_graphviz，这个也是最常用的解决方案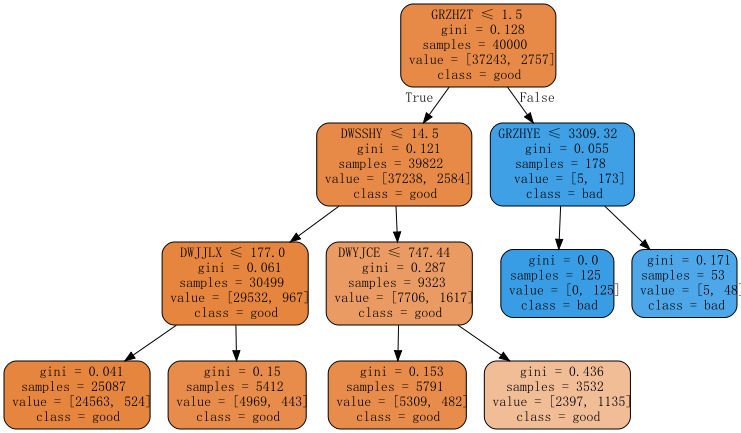
image.png

生成的决策树解释
1）samples：节点中观察的数量，比如根节点40000，表示数据集总共有4万个样本
2）有多少种类别，整棵树的叶子就有多少种颜色，比如我们这里有2个类别，颜色对应是黄、绿、Gini指数越小，该节点颜色越深，也就是纯度越高。
3）value表示当前节点2种类别的样本有多少，比如下面第一棵树的根节点，value = [37243,2757]，表示有37243个好样本，2757坏样本
4）class表示当前那个类别的样本最多，比如下面最右边的一棵树的根节点，class = bad，可以看到当前节点它的坏样本数是最多的。
5）gini：节点的基尼不纯度。当沿着树向下移动时，平均加权的基尼不纯度必须降低。

3、dtreeviz对决策树进行可视化

3.1 dtreeviz 的包详解

https://github.com/parrt/dtreeviz

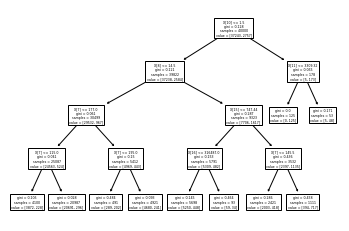
dtreeviz是我认为非常完美的决策树可视化的包，非常好理解，也非常美观。下面我们看看这个包可视化的结果。


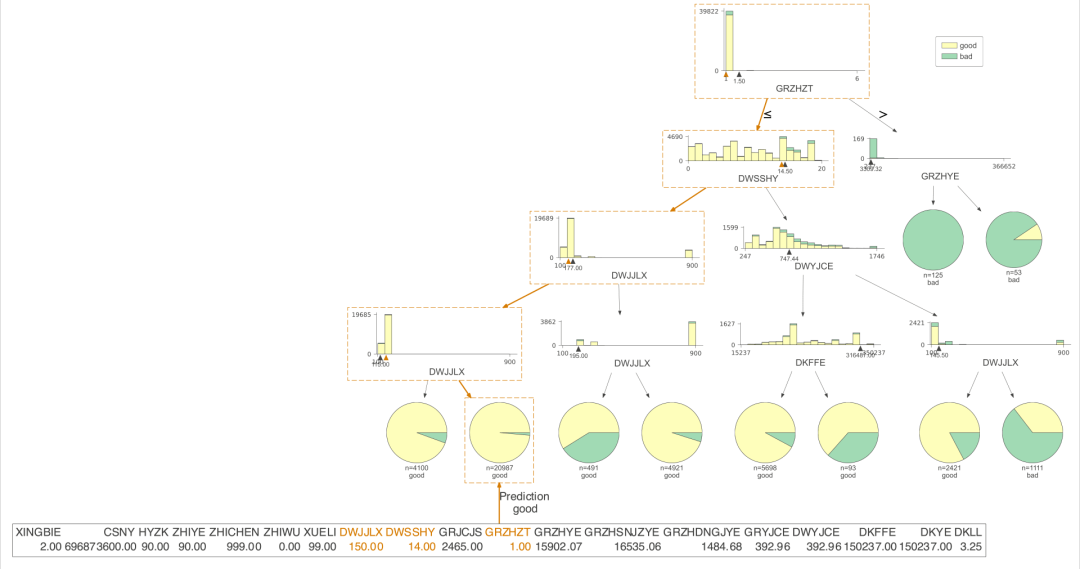
*决策树三种可视化展示形态 - 图5


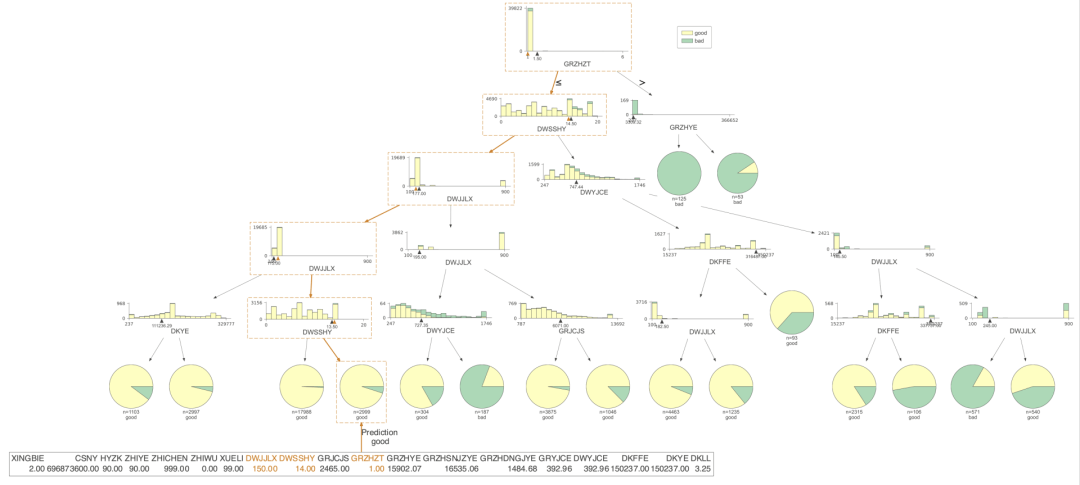
*决策树三种可视化展示形态 - 图6


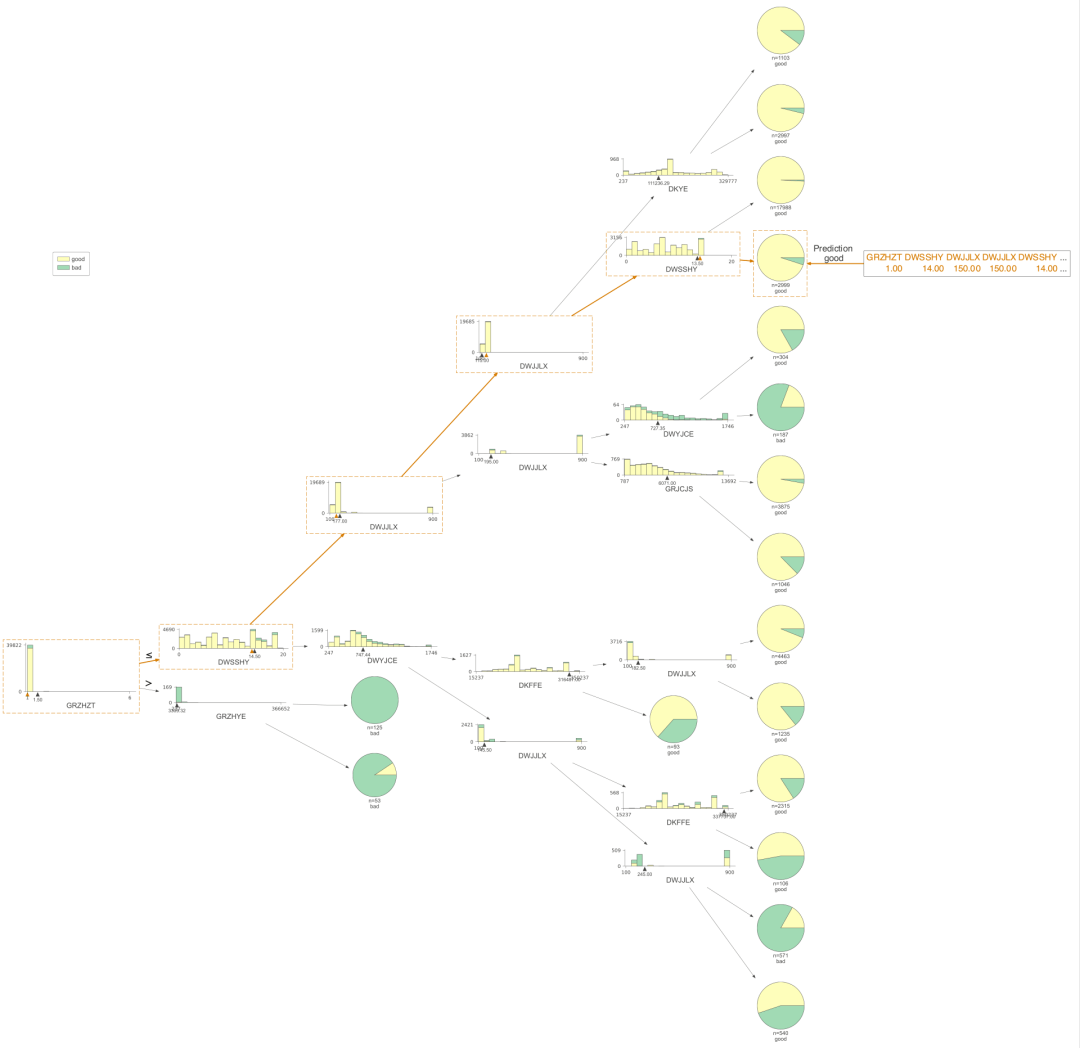
*决策树三种可视化展示形态 - 图7

只展示了预测的路径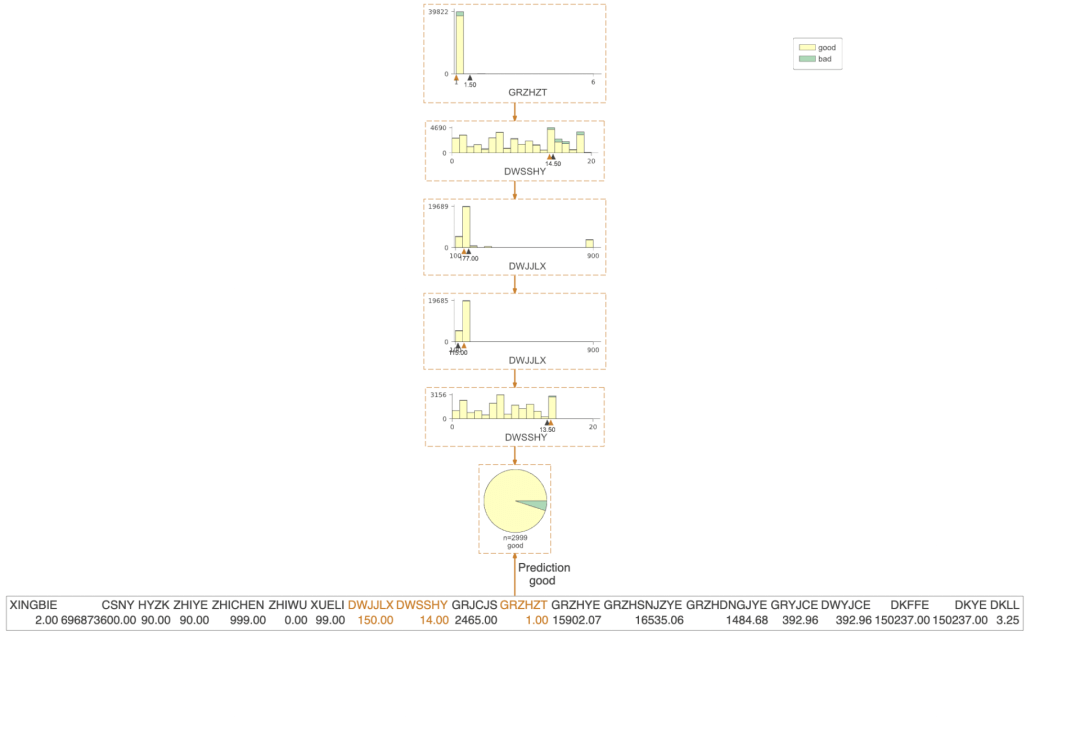
*决策树三种可视化展示形态 - 图8

有了决策树的可视化，我们就能直接得到每条策略了，当时人为的看，效率还是比较低，我们需要更高效的方式，对数据决策树上的信息进行提取，直接得到规则。

四、决策规则提取

1、决策树的生成的结构探索

要提取出来其中的规则，我们需要探索决策树的存储结构，为了探究sklearn中决策树是如何设计和实现的，以分类决策树为例，首先看下决策树都内置了哪些属性和接口：通过dir属性查看一颗初始的决策树都包含了哪些属性（这里过滤掉了以”_”开头的属性，因为一般是内置私有属性），得到结果如下：

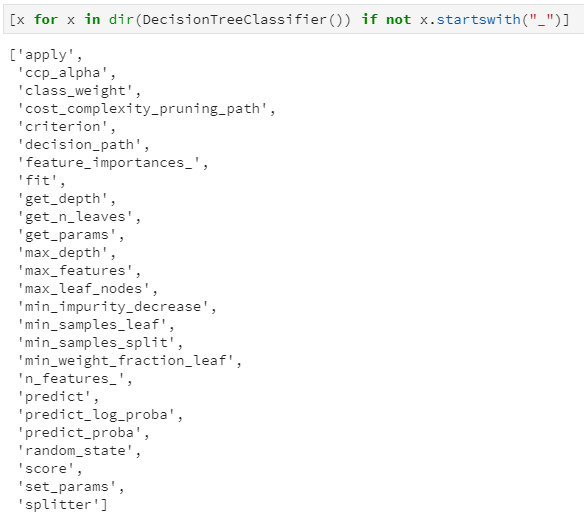
*决策树三种可视化展示形态 - 图9
大致浏览上述结果，属性主要是决策树初始化时的参数，例如ccp_alpha：剪枝系数，class_weight：类的权重，criterion：分裂准则等；还有就是决策树实现的主要函数，例如fit：模型训练，predict：模型预测等等。
本文的重点是探究决策树中是如何保存训练后的”那颗树”，所以我们进一步用鸢尾花数据集对决策树进行训练一下，而后再次调用dir函数，看看增加了哪些属性和接口：
本文的重点是探究决策树中是如何保存训练后的”那颗树”，所以我们进一步用鸢尾花数据集对决策树进行训练一下，而后再次调用dir函数，看看增加了哪些属性和接口：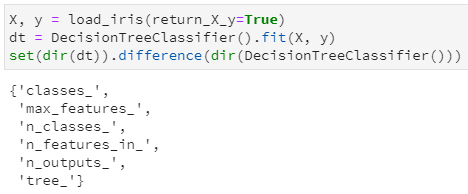
*决策树三种可视化展示形态 - 图10
通过集合的差集，很明显看出训练前后的决策树主要是增加了6个属性（都是属性，而非函数功能），其中通过属性名字也很容易推断其含义：

  • classes_：分类标签的取值，即y的唯一值集合
  • maxfeatures：最大特征数
  • nclasses：类别数，如2分类或多分类等，即classes_属性中的长度
  • nfeatures_in：输入特征数量，等价于老版sklearn中的nfeatures，现已弃用，并推荐nfeatures_in
  • n_outputs：多输出的个数，即决策树不仅可以用于实现单一的分类问题，还可同时实现多个分类问题，例如给定一组人物特征，用于同时判断其是男/女、胖/瘦和高矮，这是3个分类问题，即3输出（需要区别理解多分类和多输出任务）
  • tree：毫无疑问，这个tree就是今天本文的重点，是在决策树训练之后新增的属性集，其中存储了决策树是如何存储的。

那我们对这个tree属性做进一步探究，首先打印该tree属性发现，这是一个Tree对象，并给出了在sklearn中的文件路径：
*决策树三种可视化展示形态 - 图11
我们可以通过help方法查看Tree类的介绍：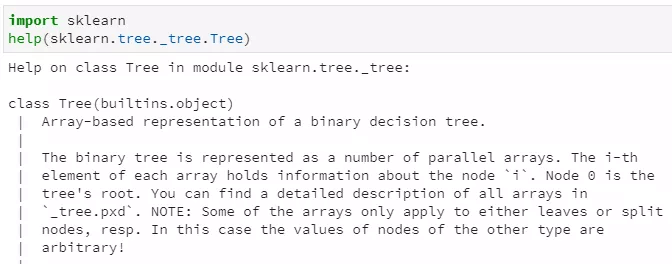
*决策树三种可视化展示形态 - 图12
通过上述doc文档，其中第一句就很明确的对决策树做了如下描述：
Array-based representation of a binary decision tree.
即：基于数组表示的二分类决策树，也就是二叉树！进一步地，在这个二叉树中，数组的第i个元素代表了决策树的第i个节点的信息，节点0表示决策树的根节点。那么每个节点又都蕴含了什么信息呢？我们注意到上述文档中列出了节点的文件名：_tree.pxd，查看其中，很容易发现节点的定义如下：
*决策树三种可视化展示形态 - 图13
虽然是cython的定义语法，但也不难推断其各属性字段的类型和含义，例如：

  • left_child：size类型（无符号整型），代表了当前节点的左子节点的索引
  • right_child：类似于left_child
  • feature：size类型，代表了当前节点用于分裂的特征索引，即在训练集中用第几列特征进行分裂
  • threshold：double类型，代表了当前节点选用相应特征时的分裂阈值，一般是≤该阈值时进入左子节点，否则进入右子节点
  • n_node_samples：size类型，代表了训练时落入到该节点的样本总数。显然，父节点的n_node_samples将等于其左右子节点的n_node_samples之和。

至此，决策树中单个节点的属性定义和实现基本推断完毕，那么整个决策树又是如何将所有节点串起来的呢？我们再次诉诸于训练后决策树的tree_属性，看看它都哪些接口，仍然过滤掉内置私有属性，得到如下结果：

  • 训练后的决策树共包含5个节点，其中3个叶子节点
  • 通过children_left和children_right两个属性，可以知道第0个节点（也就是根节点）的左子节点索引为1，右子节点索引为2,；第1个节点的左右子节点均为-1，意味着该节点即为叶子节点；第2个节点的左右子节点分别为3和4，说明它是一个内部节点，并做了进一步分裂
  • 通过feature和threshold两个属性，可以知道第0个节点（根节点）使用索引为3的特征（对应第4列特征）进行分裂，且其最优分割阈值为0.8；第1个节点因为是叶子节点，所以不再分裂，其对应feature和threshold字段均为-2
  • 通过value属性，可以查看落入每个节点的各类样本数量，由于鸢尾花数据集是一个三分类问题，且该决策树共有5个节点，所以value的取值为一个5×3的二维数组，例如第一行代表落入根节点的样本计数为[50, 50, 50]，第二行代表落入左子节点的样本计数为[50, 0, 0]，由于已经是纯的了，所以不再继续分裂。
  • 另外，tree中实际上并未直接标出各叶节点所对应的标签值，但完全可通过value属性来得到，即各叶子节点中落入样本最多的类别即为相应标签。甚至说，不仅可知道对应标签，还可通过计算数量之比得到相应的概率！

拿鸢尾花数据集手动验证一下上述猜想，以根节点的分裂特征3和阈值0.8进行分裂，得到落入左子节点的样本计数结果如下，发现确实是分裂后只剩下50个第一类样本，也即样本计数为[50, 0, 0]，完全一致。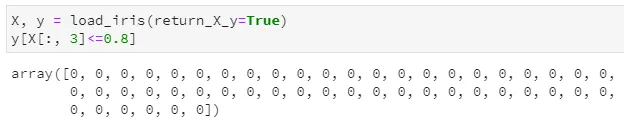
*决策树三种可视化展示形态 - 图14
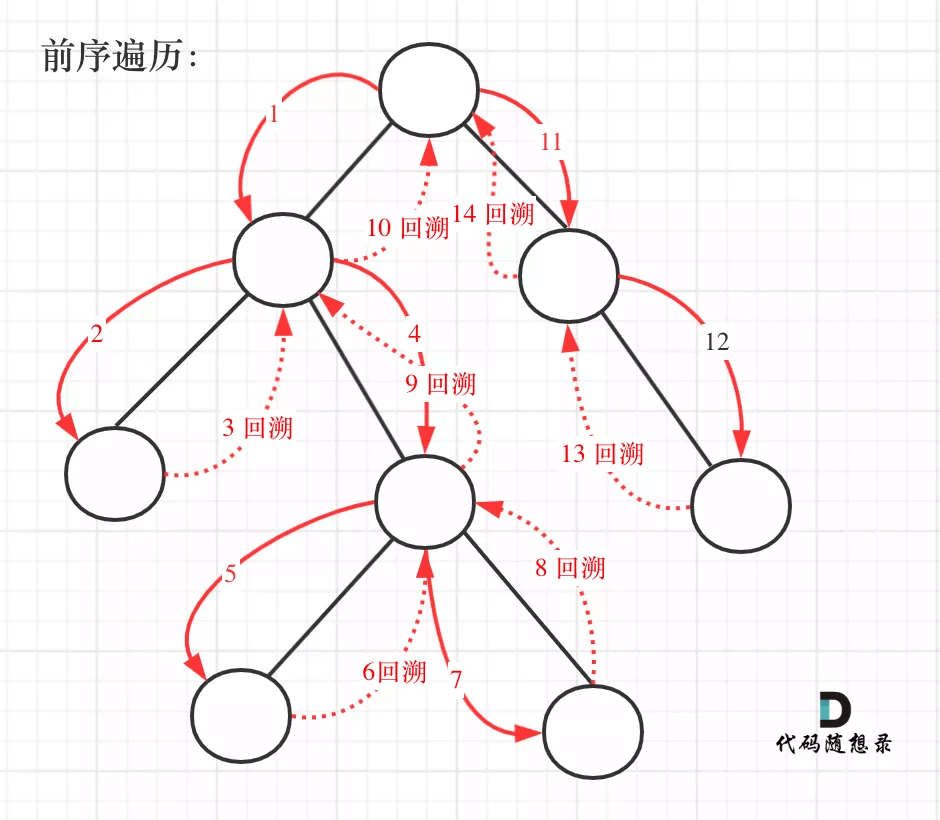
另外，通过children_left和children_right两个属性的子节点对应关系，其实我们还可以推断出该二叉树的遍历方式为前序遍历，即按照根-左-右的顺序，对于上述决策树其分裂后对应二叉树示意图如下：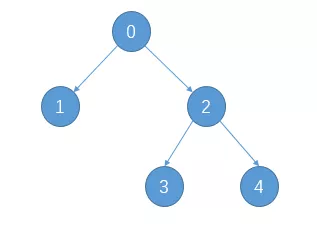
*决策树三种可视化展示形态 - 图15

2、老方法提取决策树规则

通过上面的分析，我们知道了决策树的存储方式，下面就开始规则提取，在网上搜索，基本上只能收到下面的方法：

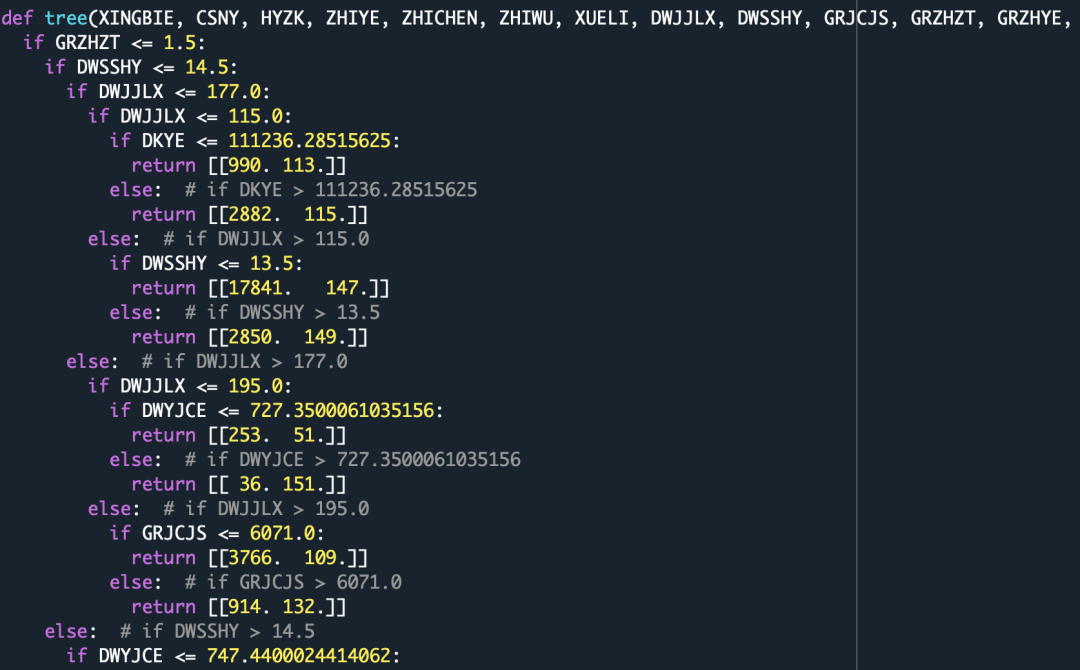
*决策树三种可视化展示形态 - 图16
’可以看得出来，虽然提取出来了策略，但是并不是很完美，还是需要人为拆解策略，于是我继续研究。

3、新方法提取决策树规则

不仅仅对对二叉树的所有路径进行遍历，还需要进行回溯并组合成变量，根据决策树的输出，构建规则提取函数，需要用到二叉树遍历和回溯算法，本人数据结构不是很好，干了两个晚上，真是编程偷不了懒，出来混迟早要还的。代码比较混乱，大家将就看，还好这个部分对效率没啥要求。如果有更好的代码，不吝赐教。
*决策树三种可视化展示形态 - 图17

*决策树三种可视化展示形态 - 图18
*决策树三种可视化展示形态 - 图19
*决策树三种可视化展示形态 - 图20