巴塞尔协议下的全面风险管理的目标是金融机构在资本约束下实现利润的最大化，而资产组合管理是全面风险管理的核心概念。资产组合管理的核心指标是风险调整后资本收益率(RAROC)和经济增加值(EVA)。公式如下：

本文基于上述思想，试图从风险损失、资产迁徙、催收运营成本角度计算资产收益情况。文章内容基于本人经验与理解，不妥之处望各位多加指正。

目录
1.数据处理
2.资产包迁徙率计算
3.资产包Vintage预估
4.资产包催收成本测算
5.单体风险收益预估

一、数据处理
首先，需要根据资产mob表计算出单个资产包截止当前时点每一期各逾期阶段的逾期个数、余额、累计逾期个数，得到一张汇总表大致如下：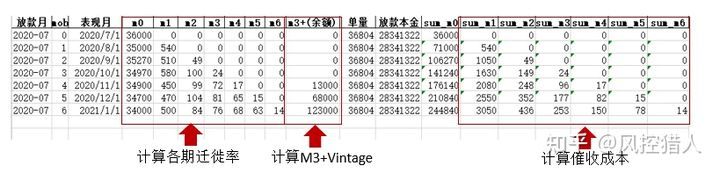

其中左侧部分为各个资产包每一期各阶段的逾期个数，基于此数据可以计算每一期的迁徙率；m3+(金额)这一列是余额，是用来计算M3+vintage数据的；右侧是累计的逾期个数，用来计算催收成本。此表基于风控mob表计算，生成的主要代码如下:
# 从mob表取数
conn=pymysql.connect(host=’’,user=’’,password=’’,db=’’)
df=pd.read_sql(‘select a.*,b.cnt,b.principalsum from ( \
select business_line 产品线,date_format(open_date,”%Y-%m”) as 放款月,mob, \
sum(case when current_cycle_status=0 then 1 else null end ) as “m0”, \
sum(case when current_cycle_status=1 then 1 else null end ) as “m1”, \
sum(case when current_cycle_status=2 then 1 else null end ) as “m2”, \
sum(case when current_cycle_status=3 then 1 else null end ) as “m3”, \
sum(case when current_cycle_status=4 then 1 else null end ) as “m4”, \
sum(case when current_cycle_status=5 then 1 else null end ) as “m5”, \
sum(case when current_cycle_status=6 then 1 else null end ) as “m6”, \
sum(case when current_cycle_status>=4 then unrecived_principal else null end ) as “m3+amt” \
from mob \
where business_line in (“XXX”) \
group by business_line,date_format(open_date,”%Y-%m”),mob)a \
inner join \
(select business_line,date_format(open_date,”%Y-%m”) as open_month,count(distinct credit_extension_app_id)as cnt,sum(principal) as principalsum \
from 成功件表 \
where business_line in (“XXX”) \
group by business_line,date_format(open_date,”%Y-%m”))b \
on a.产品线=b.business_line and a.放款月=b.open_month’,conn)

计算累计逾期个数
df.replace(np.nan,0,inplace=True)
df[‘表现月’]=df.apply(lambda x:pd.to_datetime(x[‘放款月’])+relativedelta(months=x[‘mob’]),axis=1)
df.sort_values([‘产品线’,’放款月’,’mob’],inplace=True)
df[‘sum_m0’]=df.groupby([‘产品线’,’放款月’])[‘m0’].transform(‘cumsum’)
df[‘sum_m1’]=df.groupby([‘产品线’,’放款月’])[‘m1’].transform(‘cumsum’)
df[‘sum_m2’]=df.groupby([‘产品线’,’放款月’])[‘m2’].transform(‘cumsum’)
df[‘sum_m3’]=df.groupby([‘产品线’,’放款月’])[‘m3’].transform(‘cumsum’)
df[‘sum_m4’]=df.groupby([‘产品线’,’放款月’])[‘m4’].transform(‘cumsum’)
df[‘sum_m5’]=df.groupby([‘产品线’,’放款月’])[‘m5’].transform(‘cumsum’)
df[‘sum_m6’]=df.groupby([‘产品线’,’放款月’])[‘m6’].transform(‘cumsum’)
df[‘sum_m3+’]=df.groupby([‘产品线’,’放款月’])[‘m3+amt’].transform(‘cumsum’)

二、资产包迁徙率计算
以上面的数据为例，计算资产包各期的迁徙率，此处计算的是期末的个数迁徙率，如果上图中统计的是逾期阶段的是余额而非个数，则可以计算余额迁徙率。个数迁徙率也可以采用两种方法，一种是计算当期和上一期的迁徙情况，另一种是计算当期累计和上期累计的迁徙情况，两种计算方法的结果分别如下：
计算从上一期迁徙到当期的情况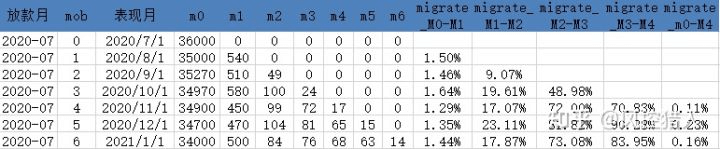

计算从上一期累计迁徙到当期累计的情况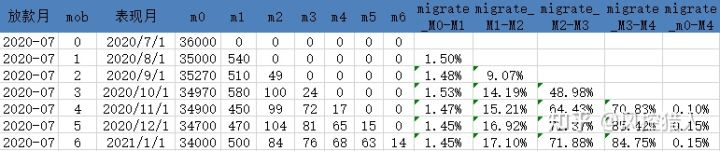

下面对比一下两种计算方式的区别，由于上面的数据已做过脱敏处理，所以对比的时候没有采用上述数据，而是采用的真实的数据。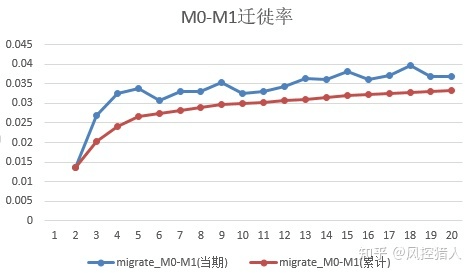

从M0-M1的迁徙率来看，资产包每一期的M0-M1迁徙率有所波动，整体趋势是在不断增高的，如果算累计的M0-M1迁徙率的话会平缓一些，但是整体趋势仍然是升高的。这种趋势的原因可以这样解释：假设第2期和第10期都产生100个M1逾期，但是第1期时的M0有1000个，到第9期时的M0只有900个。结合Vintage图解释的话，即M1+Vintage(个数)在持续走高，M1Vintage(个数)出现走平，这种情况下M0-M1迁徙率依然是升高的。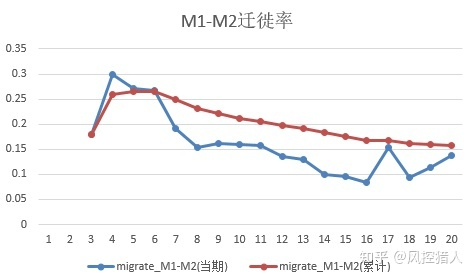

第1期迁徙率低是因为产品形态原因导致，可不作解释。整体M1-M2迁徙率的趋势是在下降的，说明越往后的资产越容易回收，这是因为越往后催收形成了一定的经验，逾期用户也形成了一定的还款习惯，且多为反复性逾期客户，所以回收率会越来越高。

三、资产包Vintage预估
以余额口径的M4+的vintage来预估每个资产包最后的损失，历史的M4+vintage如下图：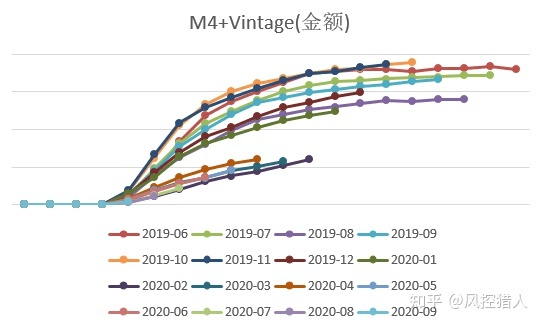

可以看到M4+vintage在12期左右开始走平。而对于未到12期的资产包，则需要通过迁徙率来预估资产包走平之后的vintage。以2020年4月份的M4+vintage为例，已有9期表现，预估其12期之后的M4+vintage的值。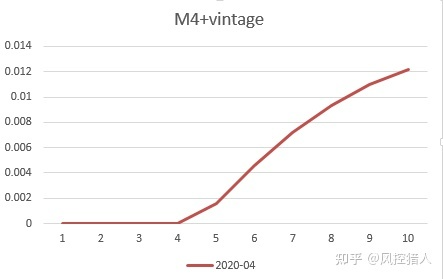

下表是这包资产每一期的逾期情况及迁徙情况。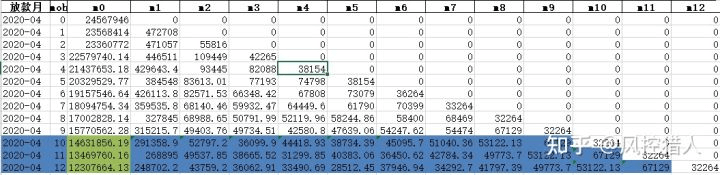


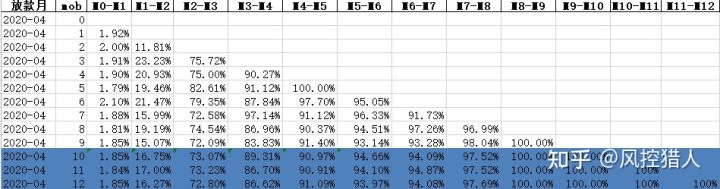
表中蓝色部分即为预测资产9期之后的表现。一共分为以下几步：
1.预测9期之后每一期的迁徙率，采用移动平均法。
2.预测9期之后每一期的M0余额，采用移动平均法。
3.将1和2预测的数据相乘，得到9期之后的资产分布情况。
基于上述步骤得到12期的M4+vintage如下：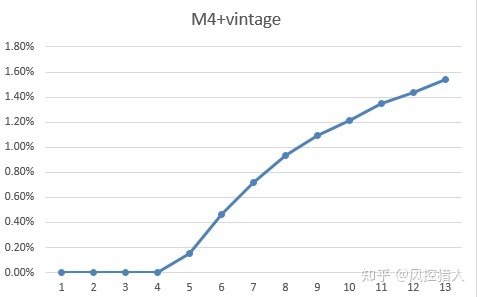

四、资产包催收成本测算
资产包催收成本和资产的vintage是强相关的，资产质量好逾期也会相应少，催收成本也相应减少。由于催收的计价方式有坐席制、计件制和费率制，不论采用何种方式计价，都可以转换成发生一次逾期所需要的费用。比如坐席制，一个坐席12000元，处理600个M1的案子，则发生一次M1逾期需要20元；如果是费率制，M1回收率90%，回收一个M1案子平均100元，按20%结佣，则发生一次M1逾期需要10020%90%=18元。M2+以上同理，可算出各逾期阶段每发生一次逾期需要花费的成本。

以上图为例，已经计算出资产包每一期的逾期个数以及逾期累计个数，按每发生一次逾期需要花费的成本与个数相乘即可计算出资产包的催收成本。
如果并不是所有客户在逾期第一天就入催，那么就需要对上图中的逾期个数进行折算。折算的过程分为两步：
1.计算出资产包每一期的缓催命中比例。
2.计算缓催期内的回收率。
有了上面两个数据则可以计算出每一期大致需要入催的比例，对上图中的逾期个数进行折算，可以对催收成本进行更加精细准确的预估。

五.单体风险收益预估
计算并预测出资产包的坏账率、催收成本后，RAROC中的分子就已经得出，大致可以看出资产包在当前vintage、迁徙率的情况下，在周期末的损失和成本，以及最终得收益为多少。因此可以提前采取针对性得措施，达到优化资产组合得目的。