来源：https://blog.csdn.net/baidu_39413110/article/details/105522672

逻辑回归评分卡因其可解释性强、上线便捷、方便管理等特点往往成为传统金融领域风险管控模型的不二选择。本篇文章就来聊一下逻辑回归评分卡的开发流程。
如果选择用python开发评分卡，经常用到的包有两个，一个是sklearn里面的LogisticRegression，一个是statsmodel里面的Logit，不管选择哪个包，我们都需要先对算法原理和拟合过程有一个理解，最好能看过源码或自己实现一下。（关于逻辑回归的python实现，具体可以参看 这篇博客）。

一、变量做WOE转换

1、WOE转换的优势

业务上做评分卡，往往不会直接去拟合变量的原始值，而是先做woe转换。变量做woe转换即把变量先分箱，然后用每箱的woe值替代原始值，然后把woe转换之后的变量拿来拟合逻辑回归。当然，理论上来讲，我们可以直接用变量原始值拟合逻辑回归，但更建议变量先做woe转换，主要因为以下几点优势：

1. 有效处理缺失值
   业务数据中很多变量不可避免会有部分缺失，缺失不一定是坏事，很多时候是否缺失本身就是很有区分度的信息，这个时候如果对缺失做均值或中位数填充，则会降低变量区分度。如果做woe转换即可以把缺失单独分一箱，有效保留了是否缺失的有效信息。
2. 对异常值不再敏感
   回归算法对异常值还是十分敏感的，有时候一个极异常点会导致整条回归拟合线的趋势反转。分箱并用woe值替代之后，异常值就不会再产生影响。
3. 对类别型变量进行了统一处理
   woe转换起到了统一处理类别型和数值型变量的作用，而且，个人认为，相比于独热编码，做woe转换是更好的处理类别变量的方式：独热编码的处理方式一是容易造成信息丢失，尤其是变量类别数过多的时候，一个类别型变量被拆分成多个0-1变量，而最后往往做不到所有0-1变量都入模，造成部分信息丢失；二是独热编码这种处理方式和变量本身的风险区分度也没啥关系。而woe转换则在这两点上具有优势，一不会造成信息丢失，二woe值也能够反映变量本身的风险区分力（区分度越强的变量，woe转换后的方差越大）。

4.起到了标准化的作用
woe转换后的变量取值都会被统一到一个量级下，变量的方差大小只和变量本身的风险区分度有关，不再受变量本身取值的影响，起到了和标准化一样的效果。如此更利于逻辑回归的拟合，在梯度下降的时候下降更快且更易找到全局最优点。

1. 非线性关系转换为线性
   最终的评分卡一定是线性的，即要么越大越好，要么越大越坏；但很多变量并不满足这种单调线性的性质，比如很多业务场景下的多头数据，会出现U型的趋势，这种U型的变量直接用来拟合逻辑回归，则很难得到一个合理的参数，而分箱woe转换后就能够将两头比较坏的人群赋予一个高woe值，中间比较好的人群赋予一个低woe值，从而让这个变量转换为线性的。当然，前提是变量本身的非线性趋势是合理的并且业务可以接受的。
2. 跟业务更好地结合
   既然我们做了分箱，就可以通过调整分箱分隔点来契合业务需求。
3. 方便评分卡的量化评估和管理
   当我们评分卡上线后，难免会遇到客群或变量偏移的情况，如果我们在开发评分卡的时候就做了分箱和woe转换，那么当某个变量发生分布偏移后，我们很容易便可以计算出客群在各个分箱之间的迁徙率，并通过系数乘以woe值量化出这种偏移对最终评分卡打分造成了多大的偏移影响。
   相应地，我们也可以通过调整变量的分箱阈值来对这种变量分布偏移进行一个人为的纠偏，至少可以让整体打分保持在一个稳定的状态。

2、为什么是WOE转换？

以上几点是woe转换在实际业务操作过程中的优势，但我们还需要深入思考一下，为什么要做woe这种形式的转换，分箱后直接用每箱的坏账率做替换不也能达到同样的效果吗？
我们知道，逻辑回归可以写成如下形式：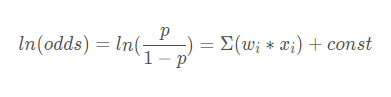

即逻辑回归是对ln(odds)的线性拟合。而woe转换即是为了和ln(odds)统一格式，让转换后的每个变量和ln(odds)之间呈现出一种单调的、线性的关系。更具体一点，woe转换后，会使得变量每增加一个单位，Odds就增加相同的值。（更详尽的解释可以参考【详解】银行信用评分卡中的WOE在干什么？）

二、相关性与多重共线性

1、相关性

在做逻辑回归拟合之前，我们都会做一步去除相关性过高的变量，为什么要这么做呢？最直观的理解就是同样维度，代表同样信息的变量不需要重复使用。那如果我们不做相关性剔除会怎样呢？
假设我们有两个变量X1和X2，真实模型是Y = X1 + X2。如果X1和X2高度相关，那我们拟合出的模型可能是Y = -2X1 + 3X2或者Y = 20X1 - 19X2，它们最终的效果和真实模型也差不多。当然单纯使用这样的模型也没有问题，但问题是拟合出的系数很病态，我们希望拟合出的每个变量的系数能够一定程度上代表这个变量对最终得分的贡献，或者至少是正贡献或负贡献能够通过系数解读出来，而不做相关性剔除的话，拟合出的系数显然不能满足我们的预期。

2、多重共线性

相关性能找出哪两个变量间高度相似，那如果某个变量和其它几个变量的线性组合高度相似怎么办呢？这种情况的存在同样会导致拟合出的系数比较病态。这个时候就需要做共线性的排查，通常我们会使用方差膨胀系数（VIF）这个指标。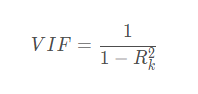

上述Rk2 代表第k个变量和其它剩余变量做回归时的判定系数。VIF这个指标说白了就是量化该变量能够多大程度上被其它变量的线性组合所解释。一般VIF为5就很高了，我们做个换算，VIF为5对应的R k 就有0.8，即剩余变量的线性组合可以解释第k个变量80%的变化特征，基本也就不需要第k个特征出现在最终的模型中了。业务操作上可以根据需求卡一个再低一些的阈值。

三、模型拟合

1、前向回归

简单说下算法逻辑：

每个变量和Y拟合一个单变量模型，根据P值或模型的卡方选择一个最优变量；
在剩余变量中选择一个最优变量入模，最优的判断标准为加入该变量后，模型的卡方最高；
重复第二步，直到剩余变量的p值都大于某个值或模型整体的卡方不再发生显著变化。

2、后向回归

所有变量入模拟合，去掉P值最高的那个变量；
剩余变量重新拟合，去掉P值最高的那个；
重复第二步直到所有变量P值小于某个阈值。
相比于前向回归方法，后向回归方法会让一些区分度相对较弱的变量有更高的几率入模。

3、逐步回归

前向回归方法选择一个最优变量入模；
加入最优变量后，重新拟合已选择的所有变量，去掉最不显著的变量（比如可以设定P值高于0.05的变量）；
重复1-2步知道变量不再发生变化。
以上方法可以帮我们找到算法上的最优解，但有时业务上往往对某些变量有硬性的入模需求，我们可以根据业务需要，把必须入模的变量做为初始变量组保留在模型中，并在此基础上再执行以上算法去选择变量。

四、 拟合结果解读

使用python做逻辑回归时，我们一般首选statsmodel这个三方包，因为它会为我们计算出一系列详细的统计检验指标，比如当我们训练好一个逻辑回归后，会得到如下这样的表格，接下来我们就来看一下这些指标都是怎么计算的以及有什么指示意义：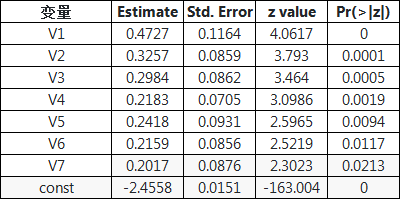

首选，estimate这一列代表的是每个变量拟合出来的系数。这里我们需要注意，除了截距const项，如果有变量的系数出现了负值，那就不太正常了。因为我们在拟合之前都对变量进行了woe转换，说明每个变量都是和y是正相关的，那系数也理应是正。如果出现了负值，说明共线性的问题没有得到有效解决，应该返回第二步继续排查一下共线性的问题再建模。
Std. Error这一列指的是拟合改变量系数时标准误差。
z value这一列是Z统计量，在统计学中，一般我们用Z表示一个具有标准正态分布的随机量。这里我们做了这样一个零假设（null hypothesis），即该变量的系数w是0，换句话说也就是w这个随机量的期望（均值）是0，根据这个假设，我们构造了一个服从标准整体分布的统计量Z：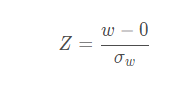

即是我们这里的z value，说白了，这个z value就是estimate这一列除以Std. Error这一列得到的。z value可以用来衡量变量的重要程度，z越大，变量的系数越显著，变量和y的关系也就越强，变量也就越重要。那么要大到什么程度才能被接受呢，一般阈值为1.96。这个1.96怎么来的呢，其实就是标准正太分布中概率为95%的取值点，解释一下就是当某个变量的z值为1.96时，它的系数为0的概率只有5%，当然我们就可以认为这个变量的系数显著不为0，即这个变量是和y有显著的相关关系的。
最后一列就是我们常看的P值，即这个变量的系数显著为0的置信度有多高，像变量V7的P值为0.0213，即变量V7的系数为0的置信度只有2%，那么我们就可以认为V7的系数在98%的置信区间上显著不为0，即V7是和y有显著相关关系的。
更详尽的解释可参看What are Z-Values in Logistic Regression?

五、分数转换

1、为什么要转换分数

很多时候评分卡都是以几百分的整数形式出现的，而不是直接使用逻辑回归输出的0-1的一个概率值。这时就需要把概率值转换一下，其实这种分数的转换并不影响模型整体的排序性，使用起来效果完全是一样的，之所以要做这种转换主要有以下两个原因：

1.更方便于跨部门的理解和使用，对于完全没有接触过统计学的人，给一个几百分的整数评分帮助他们做决断，比一堆小数来讲更容易接受。
2.有利于风控决策引擎更敏捷的计算，如果我们把分数都处理成整数了，那决策引擎在做实时计算的时候就不涉及浮点数运算，运算成本和时间都大大降低。

2、如何做转换

一般分数转换只需要我们定下来两个东西即可：
一是希望分数每增加多少，odd翻一倍；
二是在一个指定的分数上，希望odd达到多少？

接下来我们来详细解释一下：
一般转换后的分数Score和odds呈如下线性关系：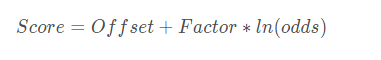

Score=Offset+Factor∗ln(odds)

我们把odds翻一倍时的分数增量称为pdo（points to double the odds），那么很容易就可以得到下列联式：

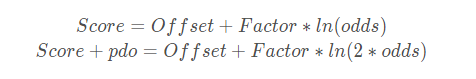
Score=Offset+Factor∗ln(odds)
Score+pdo=Offset+Factor∗ln(2∗odds)

两式相减就可以得到：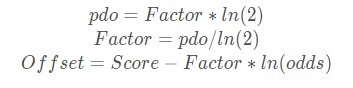

pdo=Factor∗ln(2)
Factor=pdo/ln(2)
Offset=Score−Factor∗ln(odds)

假如我们现在想要一个这样一个评分卡：每增加20分，odds翻一倍；当分数达到600分时，odds在一个50:1的水平，那么根据上述等式就可以求得：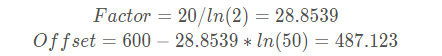

Factor=20/ln(2)=28.8539
Offset=600−28.8539∗ln(50)=487.123

如此，我们便能得到了评分卡的一个转换公式：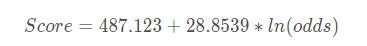

Score=487.123+28.8539∗ln(odds)

对最终计算出的Score取整之后便得到了我们业务中常用的评分卡分数。

六、可解释性

提到逻辑回归评分卡的优势，第一想到的就是可解释性好，那到底在解释什么呢？又是怎么解释的呢？
在很多机构中，当我们使用评分卡对申请人做出通过还是拒绝的判断后，往往需要对这个裁定结果给出解释，也就是让大家知道因为哪些原因做出了这样的判断。评分卡在解释这方面原因上就具有得天独厚的优势。当我们做了woe转换后，逻辑回归公式可以写成如下形式：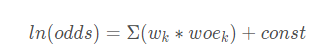

即ln(odds)是每个特征woe值乘以系数的加和，而ln(odds)和最终的评分卡得分又是线性的关系；如此，我们只需要把指定用户的每个特征的woe值乘以系数做一个排序，就能看到哪些特征对该用户的最终风险评分起到了正作用（woe乘系数符号为正），哪些变量对该用户的最终风险评分起到了负作用（woe乘系数符号为负），其中影响最大的是哪几个特征也一目了然。
当然，如果我们想把每个特征的贡献也量化成评分，也是可以做到了，只需要对Score的计算公式做个转换：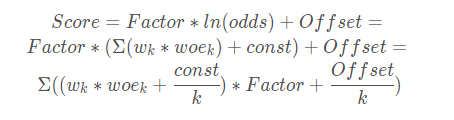

此时，为了衡量每个变量的正负贡献，我们需要先计算一个中立分数（neutral score），即woe=0时的分数（woe等于0时的分数代表用户违约的概率为50%）：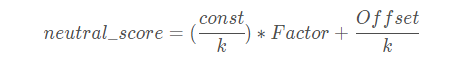

然后通过每个变量的分数和中立分数的差值来衡量每个变量的正负贡献及贡献大小。
————————————————
版权声明：本文为CSDN博主「白白的一团团」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/baidu_39413110/article/details/105522672源