本文旨在个人学习研究meta分析,仅供参考~
目录:
一、Meta分析概念
二、Meta分析流程
三、Meta分析实例
一、Meta分析概念
1.Meta分析介绍
专业术语介绍:Meta分析(Meta-analysis)是用定量的统计学方法分析、综合、概括各研究结果的一种系统评价(定量系统评价),是用于比较和综合针对同一科学问题研究结果的统计学方法,其结论是否有意义取决于纳入研究的质量,常用于系统综述中的定量合并分析。与单个研究相比,通过整合所有相关研究,可更精准地估计医疗卫生保健的效果,并有利于探索各研究证据的一致性及研究间的差异性。而当多个研究结果不一致或都无统计学意义时,采用Meta分析可得到接近真实情况的统计分析结果。
通俗点:就是对多个具有相同研究目的独立研究结果进行系统的、定量综合的一种研究方法,集大家所言统一出一个结论。
2.Meta分析来源
源于Fisher 1920年合并P值的思想,1976年由心理学家Glass进一步发展为合并统计量,并命名为“meta-analysis”,国内也称为“荟萃分析”。广泛用于医学研究各领域:病因研究、临床试验、诊断、治疗和预后研究。20世纪80年代中期,Meta分析被逐步引入到临床随机对照试验及流行病学研究中,并在近十年来快速发展,Meta分析论文发表数量也快速增长。近年来,随着方法学的不断发展,累积Meta分析(CumulativeMeta analysis)和网状Meta分析(NetworkMeta analysis)等新方法也应运而生。
3.Meta分析的内容
Meta分析的内容有:①异质性分析及处理多个独立研究的统计量一致性检验;②合并效应值计算;③合并效应值的检验
异质性检验是Meta分析的重要环节,多用Q检验确定多个独立研究的异质性是否具有统计学意义,一般认为当P>0.1时,各独立研究结果一致性较好。
效应值的选取通常根据临床研究的性质、资料的类型确定。Meta分析合并效应值常用统计模型有固定效应模型和随机效应模型两种,当多个研究具有同质性时,采取固定效应模型;当多个研究不具有同质性时,对异质性原因进行分析和处理,如进行亚组分析,若异质性分析和处理后仍无法解决时,可采取随机效应模型进行合并效应值的计算。
针对合并效应值进行假设检验,以检验多个同类研究的合并效应值是否具有统计学意义。常用方法如下:①z(u)检验:若P≤0.05,多个研究的合并统计量具有统计学意义;②置信区间法:当试验效应指标为OR、RR时,其95%可信区间若不包含1,等价于P<0.05,即有统计学意义。当试验效应指标为RD、SMD时,其95%可信区间若不包含0,等价于P<0.05,即有统计学意义 。
4.Meta分析目的
- 增加统计学检验效能
- 定量估计研究效应
- 发现既往研究的不足
5.Meta分析优缺点
优点:
①实现定量综合;②对同一问题提供系统的、可重复的的综合方法;③通过对同一主题多个小样本研究结果的综合,提高原结果的统计效能;④解决研究结果的不一致性,改善效应估计值;⑤回答各项原始研究未提出的问题;⑥探究现有文献发表偏倚的程度;⑦提出新的研究问题,为进一步研究指明方向。
缺点:
①当原始研究质量不高时,Meta分析可能无意义,合并的结果还会遭受“垃圾进、垃圾出”的质疑。原始文献的质量是系统综述的保证,对于质量欠佳的临床证据,应充分认识其局限性,辩证对待,并有针对性地开展高质量的临床研究,完善和丰富证据资源。
②当各原始研究中存在临床差异时,在单一Meta分析中合并所有纳入研究并无意义,如进行不同治疗措施与对照措施间的混合比较时需要考虑每一个比较的合并,此时合并的决策不能依从于统计方法而需要讨论和临床判断。
在文献查找、选择、数据提取和统计分析过程中,如果处理不当,还会引入新的偏倚,导致合并后的结果歪曲了真实的情况,如存在发表偏倚(Publicationbias):即具有统计学显著性研究意义的研究结果较无显著性意义和无效的结果被报告和发表的可能性更大。而对存在偏倚风险的研究进行Meta分析可能产生严重误导,产生“错误”结果。
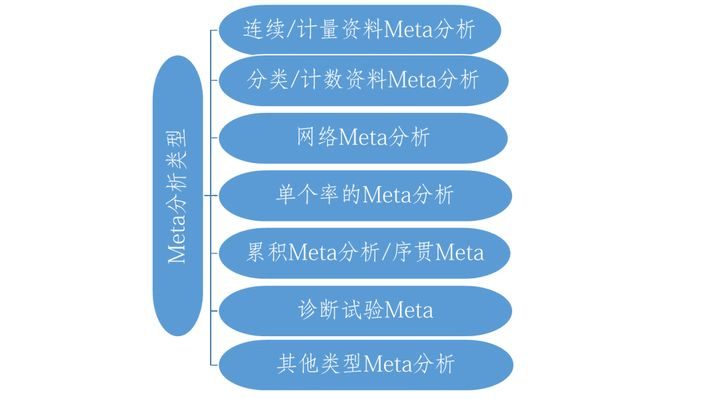
6.Meta分析类型
7.什么时候我们可以考虑做meta分析
首先任何研究的意义肯定都是为了解释目前还没有明确阐明的问题:
- 比如目前单个研究样本量太小,无法得出统计学意义的结论,可以通过meta更精确的评估总效应;
- 比如目前研究得到的结论不一致,可以通过更精确的亚组meta分析,讨论异质性结论的原因;
- 比如想统计大范围的流行病学数据,比如某个疾病的在全国或某个区域的发病率。如果开展大范围的调研是很难的,可以通过mata分析将单个率的效应量合并,纠正因小样本带来的研究偏移。
二、Meta分析流程
1.Meta分析步骤概览
- 选题
- 文献检索
- 文献纳入与排除
- 文献质量评价
- 数据及相关信息提取
- 异质性分析
- 效应量选择
- 发表偏倚分析
2.选题
选题决定了meta分析的意义,一个好的选题应该立足实际并且具有指导意义、创新价值。
PICOS法则:
P(Population)研究对象 :需要研究的对象人群或代表与研究对象相关的问题。
I(Intervention)干预措施:对研究人群采用的治疗干预措施或与观察指标。
C(Comparison)比较组:代表对照组和将给予治疗措施或观察的指标。
O(Outcome)结局:代表与结局指标和相关的问题。
S(Study design)研究类型:即研究设计是什么,队列研究、病例对照还是横断面。
3.文献检索
meta分析是对一主题已有的研究进行的综合分析,所以应该尽可能全面、系统地收集相关文献进行文献检索。
(1)文献检索策略
关键词、检索范围、检索方式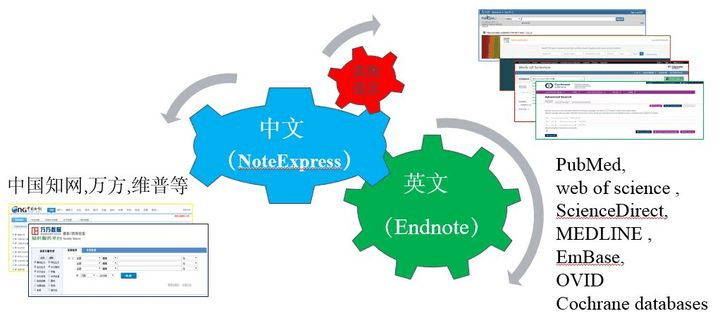
(2)检索步骤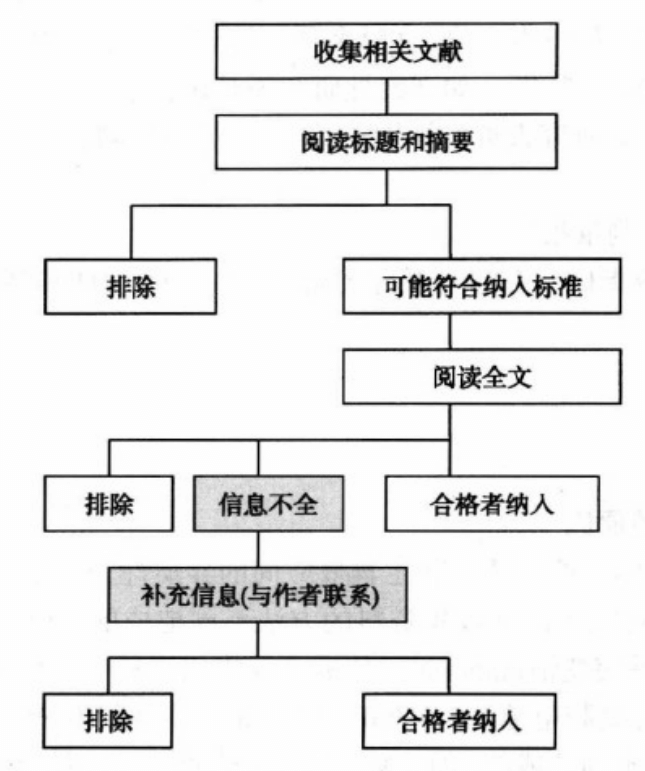
【 检索实例】
Are weight loss interventions associated with changes in biomarkers of liver disease in people with nonalcoholic fatty liver disease?
第一步,首先确定研究对象、干预措施以及研究类型的主题词及以自由词
研究对象:nonalcoholic fatty liver disease
主题词:nonalcoholic fatty liver disease
自由词:Non alcoholic Fatty Liver Disease / NAFLD / Nonalcoholic Fatty Liver Disease
Fatty Liver, Nonalcoholic/Fatty Livers, Nonalcoholic/Liver, Nonalcoholic Fatty/Livers, Nonalcoholic
Fatty/Nonalcoholic Fatty Liver/Nonalcoholic Fatty Livers/Nonalcoholic Steatohepatitis/Nonalcoholic
Steatohepatitides/Steatohepatitides, Nonalcoholic/Steatohepatitis, Nonalcoholic
干预措施:weight loss
主题词:weight loss
自由词:Weight Reduction Programs/ Diet, Reducing
研究类型:RCT
主题词:Randomized Controlled Trials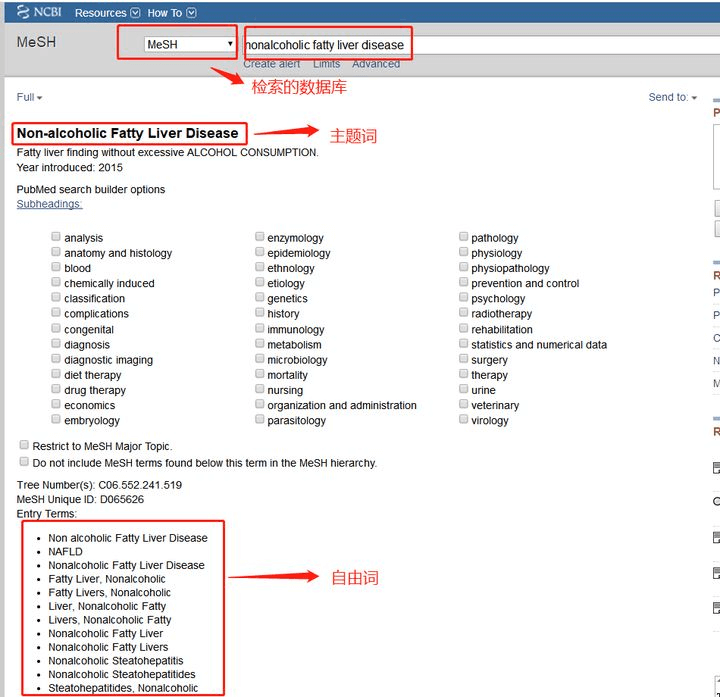
第二步:主题词+自由词,进行检索(以Pubmed检索为例)
4.文献纳入与排除
在做这一步时候需要制定好纳入与排除的标准。
可能考虑的因素:
- 研究类型和目标
- 文献时间和语言
- 样本量和随访期限(观察期)
- 测量指标
- 是否有重复发表的内容
- 信息完整性
5.文献质量评价
选用针对某一类专有研究的评价方法,比如临床上:Consort声明(CONSORT工作小组制定的临床试验报告规范)、Jadad标准(是独立评价临床试验方法学质量的工具)等……
6.数据及相关信息提取
1.文献的基本信息 如发表刊物、文献名称、作者名称、发表年代等。
2.研究的类型和方法学特征 如观察性研究还是试验性研究。
3.研究对象特征 如研究人群的性别年龄和种族等基本特征,患者的诊断标准及对照的选择标准等等。
4.干预措施和结局测量指标。
5.meta分析的效应指标 有的可以直接从文献中获取,有的需要经过对文献中的数据进行计算后获得。
6.样本含量等。
提取数据:制定纳入排除标准,筛选数据,并提取数据
1)文献筛选:由两名以上作者盲法独立筛选文献,如果有不一致文献时,请专家等第三人进行评议
2)提取数据:根据具体研究制定表格,使各篇文献中提取到的信息形成结构化数据集,收集包括作者、发表年份、研究对象性别、年龄等研究特征以及受试者特征;干预措施、场所(医院、社区)及研究的结局指标(包括主要结局指标以及次要结局指标)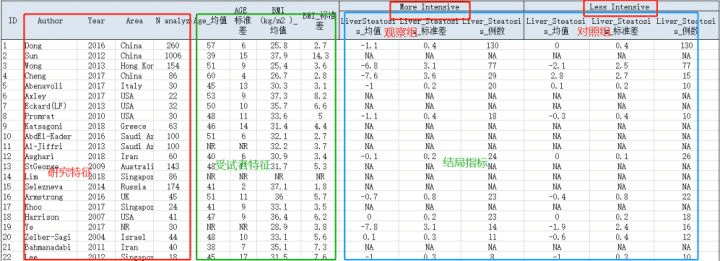
7.异质性分析
(1)先讲述下异质性是个啥?
异质性(Heterogeneity)是指一些事物在某些特征上存在差异。在Meta分析中,异质性指纳入的不同研究之间存在的差异。当研究间存在异质性时,合并的结果可能是不可靠的,或合并本身就是不恰当的。因此在做Meta分析时,需要识别和测量异质性,并制定相应的策略探索异质性。
meta分析必须考虑到异质性,并且对异质性进行探索和分析,了解导致异质性的原因,同时尽量选择无异质性,同质性高的研究进行合并。我们所讲的异质性,包括了临床异质性,方法学异质性以及统计学异质性。
(2)异质性产生的原因
总的来说分为方法学上的异质性和生物效应间的异质性。方法学异质性是指同一主题研究方法不同,选择的对照不同或收集资料的方法不同造成的。(例如有研究在xxx基因在xxx疾病的种系突变情况的meta分析中收集的文献中基因突变的检测方法就有3种,直接测序、变性梯度凝胶电泳法(DGGE)聚丙烯酰胺凝胶电泳法。)生物学效应异质性是由于研究人群的特征不同造成的,如年龄、性别和种族等。(例如研究Xxx基因多态性与xxx疾病的关联性meta分析,一般要按种族分层分析。)
(3)异质性检验
有多种统计学方法可检测研究间的异质性,如CochraneQ检验,计算P值;也可以使用直观的图示方法检测异质性,如L'AbbéPlot。
(4)异质性分析方法
若发现异质性,如当P≥50%时不宜行meta分析,此时最常用的方法为描述性系统评价或使用亚组分析或meta回归等探讨异质性来源。
1.亚组分层分析 分层因素可按方法学或生物学特征进行。如按人群的种族分或按指标的测量方法分。但是不宜过多分层。
2.meta回归 若影响因素多,不宜用分层方法时,可采用Greenland在1987年根据回归分析的基本思路提出的meta回归方法。
对于同质性较好的研究宜采用固定效应模型分析;对存在较明显异质性的研究,应使用随机效应模型合并。但是事实上无论存不存在异质性,现在都趋向采用随机效应模型,因为随机效应模型计算所得可信区间较固定效应模型为大,结果更为“保守”。
8.效应量选择
研究中常用的效应量指标包括:
1.连续型变量资料有WMD(加权均数,weighted mean difference)和SMD(标准化均差 standardized mean difference)。
2.二分类资料的效应值指标有相对危险度(relativeriskRR) 比值比(oddsratioOR)危险度差值(riskdifference,RD)。
3.若为等级资料或多分类资料,由于受方法学限制,数据需要转化成上述两种类型。
4.生存资料的效应指标是危险比(hazardratioHR)有时候也可当作二分类变量处理,采用RR、OR、RD。
9.发表偏倚分析
发表偏倚是meta分析最常见的系统误差。由于阳性结果比阴性结果更容易发表,形成了为数不少的“抽屉文件”,根据发表文献所做的综合分析有可能歪曲了真实效应。据调查统计,临床试验报告阳性结果的发表率约为77%,而阴性结果发表率仅为42%。因此,在 meta分析中必须对发表偏倚进行讨论。
(一)如何发现发表偏倚
1.漏斗图(funnel plots) 是从直观上识别发表偏倚的方法。漏斗图的横坐标为原研究的效应量,若为连续性变量可直接用原始测量值,若为关联性指标可用自然对数转换后的值。纵坐标为原研究的样本量,或标准误或精确度(标准误的倒数)。样本量越小,分布越分散;样本量大,分布越集中。若没有偏倚,呈对称的漏斗状。相反,图形不对称有偏向,表示存在偏倚。
2.线性回归法和秩相关法常用的有Egger法和Begg法,实质上是用统计学方法对漏斗图的对称性进行检验,有研究认为当纳入研究数较少或发表偏倚较小时,Egger较Begg更敏感。
3.Rosenthal抽屉文献法又称失安全系数。其原理是计算最少需要多少个未发表的阴性研究才能使meta分析的阳性结论逆转。因此,失安全系数越大,说明发表偏倚越小, meta分析结果越稳定。
4.剪补法(Duval and Tweedie trimand fillmethod)其基本思想是在漏斗图不对称的基础上,剪去不对称部分,然后沿中心两侧粘补上被剪切部分及相应的遗漏部分,最后基于剪补后的漏斗图进行效应量合并;观察剪补前后效应量的改变,从而估计发表偏倚对meta分析结果的影响。
(二)发表偏倚的控制
由于发表偏倚发生在研究设计和资料收集阶段,因此在设计阶段制定合理的纳入和排除标准:在资料收集阶段尽量全面系统地收集文献,包括发表、未发表和信息不全的,以控制发表偏倚。
三、Meta分析实例
1.实例分析—-气候变化对中国主要粮食作物单产影响的文献计量Meta分析
参考:
文献检索并采集数据:
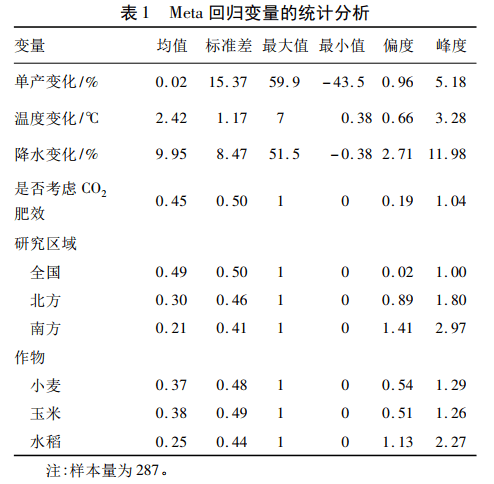
meta回归:


2.实例分析—-戒烟对肺功能的影响
肺功能的检测是COPD诊断和病程进展评估的最为重要的指标,因此戒烟对COPD发病和死亡的影响作用可以通过肺功能的研究得到一个初步结论。目前戒烟的作用相比持续吸烟者来说,不同研究的结论有所差异。而且在一些人群中认为,如果是长期吸烟者,突然戒烟会造成机体功能紊乱,死亡时间可能提早。因此,本文将应用系统综述的方法,对中国大陆地区所有已发表在专业杂志上的有关文献进行相关meta分析,对戒烟对肺功能 FEV1,FEV1%,FVC,MMEF ,MVV和RV/TLC%等肺功能指标的影响进行了定性和定量的分析。
收集1989~2005年间国内外公开发表的中国大陆关于吸烟、戒烟和肺功能关系的研究文献。总共检索到相关文献169篇,经过阅读摘要和题名筛检出了26篇关于吸烟和戒烟与肺功能关系的研究经过研究小组严格的文献质量评价后其中有7篇文献纳入了Meta分析。
1)以FEV1%为例,SAS软件实现效益量合并的过程如下,表1(合并文献的效应参数)。
表1 纳入Meta 分析的文献参数
| Study ID | smoking cessation N | smoking cessation Mean | smoking cessation SD | smoking N | smoking Mean | smoking SD |
|---|---|---|---|---|---|---|
| daizhenshou06 | 51 | 80.10 | 5.50 | 18 | 75.00 | 5.10 |
| huangbo10 | 17 | 80.10 | 10.32 | 17 | 79.54 | 9.40 |
| sub-10 | 14 | 79.02 | 9.40 | 14 | 75.45 | 8.94 |
| wangping02 | 58 | 76.60 | 4.60 | 32 | 66.70 | 4.20 |
| wangxiaoge12 | 24 | 80.46 | 2.48 | 24 | 63.32 | 1.76 |
| zhanghongwen09 | 100 | 86.60 | 14.30 | 100 | 84.30 | 15.20 |
| zhaochunbi08 | 29 | 76.20 | 7.90 | 38 | 62.70 | 9.10 |
2)SAS程序:
data a ;
input n1 x1 st1 n2 x2 st2; /n1 n2 st1 st2 ;/分别为戒烟和吸烟样本,均数和标准差/ ssc=sqrt(((n1-1)st1**2+(n2-1)st2**2)/(n1+n2-2)); /计算各研究合并标准差/
di=(x1-x2)/ssc; /计算各研究合并均差/
wi=n1+n2; /权数/
wid=widi; /加权均差/
wid2=widi**2;
s_num=7;
cards; /输入各研究原始数据*/
51 80.10 5.50 18 75.00 5.10
17 80.10 10.32 17 79.54 9.40
14 79.02 9.40 14 75.45 8.94
58 76.60 4.60 32 66.70 4.20
24 80.46 2.48 24 63.32 1.76
100 86.60 14.30 100 84.30 15.20
29 76.20 7.90 38 62.70 9.10
;
data b;
set a;
swi1+wi; swid1+wid; swid21+wid2; /计算合计权数,加权均数差/
id=n;
if n=s_num then do;
swi=swi1;swid=swid1;swid2=swid21;
end;
run;
proc sort; /将计算结果显示在第一行/
by descending id;
run;
data c;
set b;
avd=swid/swi; /avd为平均加权均数差/
sd2=(swid2-avd*2swi)/swi; /加权方差
se2=4*s_num/swi(1+avd**2/8);
chisq=s_numsd2/se2;df=s_num-1; /齐性检验的chi值和自由度/
p=1-probchi(chisq,df); /齐性检验的P值/
if sd2>se2 then sdel2=sd2-se2; /sdel2随机效应总体方差/
else sdel2=0;
low=avd-1.96*sdel2**0.5;
up=avd+1.96*sdel2**0.5;
sdbar=se2**0.5/s_num**0.5; /sdbar 为效应量加权均数的标准误/
flow=avd-1.96*sdbar;
fup=avd+1.96*sdbar; /flow fup ,low up 分别为固定效应和随机效应的95%CI上下限/
proc print;
run;
3)结果输出显示如下:
Obs n1 x1 st1 n2 x2 st2 ssc di wi wid wid2
1 29 76.20 7.90 38 62.70 9.10 8.6036 1.56911 67 105.130 164.96
2 100 86.60 14.30 100 84.30 15.20 14.7569 0.15586 200 31.172 4.86
3 24 80.46 2.48 24 63.32 1.76 2.1503 7.97080 48 382.598 3049.62
4 58 76.60 4.60 32 66.70 4.20 4.4632 2.21815 90 199.633 442.82
5 14 79.02 9.40 14 75.45 8.94 9.1729 0.38919 28 10.897 4.24
6 17 80.10 10.32 17 79.54 9.40 9.8707 0.05673 34 1.929 0.11
7 51 80.10 5.50 18 75.00 5.10 5.4013 0.94421 69 65.151 61.52
swi1 swid1 swid21 id swi swid swid2 avd sd2 se2
536 796.511 3728.12 7 536 796.511 3728.12 1.48603 4.74716 0.066659
469 691.381 3563.16 6 .
269 660.209 3558.30 5 .
221 277.610 508.68 4 .
131 77.977 65.87 3 .
103 67.080 61.63 2 .
69 65.151 61.52 1 .
chisq df p sdel2 low up sdbar flow fup
498.513 6 0 4.68051 -2.75433 5.72639 0.097584 1.29476 1.67729
经齐性检验结果显示P<0.000,采用随机效应模型计算可信区间结果std=1.48(-2.75,5.72) ,效应值可信区间包含了无效效应值零,故本研究经合并效应量不认为戒烟对肺功能FEV1%具有明显的改善作用。
(四):四格表资料的Meta 分析程序
4)以一项胆固醇水平高低与冠心病关系的META分析为例。
表2资料列举了9项胆固醇水平与冠心病的关系的研究原始资料和部分输出结果; 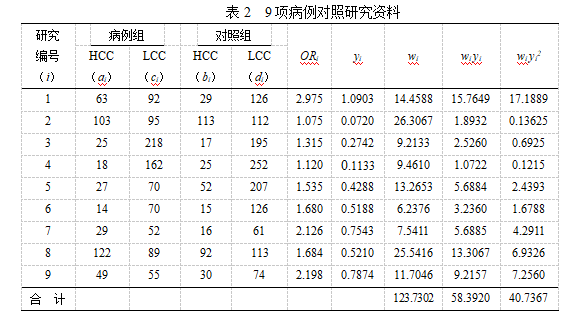
运行表3的程序输出Q值为13.18,P为0.105,齐性检验结果提示采用固定效应模型合并统计量cOR及其95%CI;cOR=1.63539 (1.29400 ,2.0668);
分析结果提示高胆固醇组人群冠心病的发病危险是低胆固醇组人群的1.63倍。
5)表3 SAS程序:
| data a ; input ai bi ci di; OR=(aidi)/(bici); yi=LOG(OR); wi=(1/ai+1/bi+1/ci+1/di)(-1); ni=ai+bi+ci+di; s_num=9; cards; 63 92 29 126 103 95 113 112 25 218 17 195 18 162 25 252 27 70 52 207 14 70 15 126 29 52 16 61 122 89 92 113 49 55 30 74 ; data b ;set a ; wi2=wi**2;wiyi=wiyi;wiyi2=wiyi**2; swi1+wi;swi21+wi2; swiyi1+wiyi;swiyi21+wiyi2; Id=n; if n=s_num then do ; swi=swi1;swi2=swi21; swiyi=swiyi1;swiyi2=swiyi21; ywbar=swiyi/swi;sybar2=1/swi; Q=swiyi2-ywbar**2*swi; smu2=(Q-s_num+1**)/(swi-swi2/swi); end; |
P=1-probchi(Q,snum-1); proc sort; by descending Id; data c;set b; forc=exp(ywbar); forlow=exp(ywbar-1.96*sybar2**0.5); forup=exp(ywbar+1.96*sybar2**0.5); smu2s+smu2; wis=1/(wi(-1*)+smu2s); wisyi=wisyi; swis1+wis;swisyi1+wisyi; if _n=s_num then do; swis=swis1;swisyi=swisyi1; ybar=swisyi/swis; sy2=1/swis; ORc=exp(ybar); orlow=exp(ybar-1.96*sy2**0.5); orup=exp(ybar+1.96*sy2**0.5); end; proc print; run; |
|---|---|
3.实例分析—-应用PROC MCMC过程实现网状Meta分析 SAS相关代码:
马尔科夫 - 蒙特卡洛(Markov Chain Monte Carlo, MCMC)算法
对四种药物进行分析:
Data betablock1; / 建立名称为“betablock1”的数据集 /
input Study ar an br bn cr cn dr dn;
/9个变量 其中8个是4个药物的 study相当于ID/
datalines;
1 0 0 35 62 37 61 0 0
2 73 152 83 154 76 150 0 0
3 0 0 0 0 81 122 93 126
4 66 124 0 0 78 122 66 118
5 55 121 0 0 77 120 79 119
6 24 70 15 33 0 0 0 0
7 10 19 31 54 0 0 0 0
8 0 0 57 92 0 0 70 96
9 18 78 132 285 0 0 0 0
10 92 336 125 335 0 0 0 0
11 0 0 63 144 0 0 73 142
12 0 0 35 120 0 0 48 118
13 0 0 84 119 0 0 85 117
14 41 98 52 103 0 0 0 0
15 37 102 45 104 0 0 0 0
16 49 150 0 0 0 0 77 149
17 43 129 0 0 0 0 65 132
18 45 129 0 0 0 0 70 129
19 13 116 0 0 0 0 26 111
20 96 376 0 0 0 0 126 371
21 16 49 0 0 0 0 19 49
;
run;
/“Itrt”编入索引是为了在 proc MCMC 过程中使用 (1=A,2=B, 3=C,4=D);/
/“Recordis”是一个在 MCMC 随机效应模型中使用的独立、连续的标示符 /
data betablock2;
set betablock1 end=myend;
length Trt $ 8;
retain Nreff 0 NTrtlev 0 Nstudy 0; /retain 变量 0 相当于不保留这个变量/
drop ar an br bn cr cn dr dn Ntrtlev Record Nreff NStudy;
retain record 0;
Narm= (ar+an >0) + (br+bn >0) + (cr+cn >0)+(dr+dn>0) ;
if ar+an >0 then do;r=ar;n=an;Trt=”A”;ITrt=1;record=record+
1;output;end;
if br+bn >0 then do;r=br;n=bn;Trt=”B”;ITrt=2;record=record+
1;output;end;
if cr+cn >0 then do;r=cr;n=cn;Trt=”C”;ITrt=3;record=record+
1;output;end;
if dr+dn >0 then do;r=dr;n=dn;Trt=”D”;ITrt=4;record=record+
1;output;end;
Nstudy=Nstudy+1;Nreff=Nreff+6-1;NTrtlev=max(Ntrtlev,6);
/ 标记 1/
if myend then do;
call symput(“Nrec”,record);
call symput(“Nreff”,Nreff);
call symput(“NTrtlev”,NTrtlev);
call symput(“NStudy”,NStudy);
end;
run;
/ 去除各数据前端的空格 /
%let Ntrtlev=&Ntrtlev; %let Nstudy=&Nstudy; %let
Nreff=&Nreff; %let Nrec=&Nrec;
/ 展示各个数据 /
%put Nrec= &Nrec; %put Nreff= &Nreff; %put NTrtlev=
&NTrtlev; %put NStudy= &NStudy;
/ 产生虚拟数据保证程序顺利计算 /
data a; run;
/ 随机效应模型计算 /
Title1 “ 随机效应模型 PROC MCMC 过程 “;
/ 下面的代码将运行 PROC MCMC 过程并使所有数据读入矩阵且保证不会重复读取 /
proc mcmc data=a monitor=(beta2-beta&Ntrtlev LogOR OR sd v) STATISTICS(PERCENTAGE=(2.5 5 25 50 75 95 97.5))=ALL
NTU=10000 NBI=10000 NMC=1000000 thin=100
jointmodel;
array beta[&Ntrtlev] beta1-beta&Ntrtlev;
array alpha[&Nstudy] alpha1-alpha&Nstudy;
array LogOR[&Ntrtlev];
array OR[&Ntrtlev];
array randeff[&NReff] Randeff1-Randeff&NReff;
array reffwt[&Ntrtlev,%eval(&Ntrtlev -1)];
array reffind[&Nrec];
array reffpt[&Nrec];
/ 内部存储的数据 /
array Study[1]/nosymbols; array r[1]/nosymbols; array n[1]/
nosymbols;
array itrt[1]/nosymbols; array Narm[1]/nosymbols;
/ 固定效应模型约束 /
BEGINCNST;
/ 读取数据进入工作空间 /
rc = read_array(“betablock2”, Study, “Study”);
rc = read_array(“betablock2”, R, “r”);
rc = read_array(“betablock2”, N, “n”);
rc = read_array(“betablock2”, itrt, “itrt”);
rc = read_array(“betablock2”, Narm, “Narm”);
Nrec=dim(Study,1);
/k 是指定当前的研究 /
k=0;
reffpoint=0;
kk=1;
do i=1 to &nrec;
/ 抵消该研究的第一个随机效应 ; 检查是否有重复纳入研究 /
if k=Study[i] then do; kk=kk+1; end;
else do; k=Study[i]; reffpoint=reffpoint+kk-1; kk=1;
end;
reffind[i]=reffpoint;
reffpt[i]=kk;
end;
/ 此处定义约束条件 ; 该部分被设计得很灵活 , 以至可用于任何不同的约束条件 /
do i=1 to &Ntrtlev;
do j= 1 to i-2; reffwt[i,j]=sqrt(1/(2j(j+1))); end;
if i>1 then reffwt[i,i-1]=sqrt(i/(2(i-1)));
do j= i to %eval(&Ntrtlev-1); reffwt[i,j]=0; end;
end;
**;
beta[1]=0;
ENDCNST;
/ 指定先验和初始值 /
parms alpha: 0;
parms beta2-beta&Ntrtlev 0;
parms sd 1;
parms Randeff: 0;
prior sd ~ uniform(0.001,10);
v=(sdsd);
/ 保证先验的合理性 /
prior Randeff: ~ normal(0, var = v);
prior alpha: ~ normal(0, var = 10000);
prior beta2-beta&Ntrtlev ~ normal(0, var = 10000);
ll=0;
do i=1 to &nrec;
/ 二进制数据 ; 这里的随机效应是该试验不受约束的随机效应的加权总和 /
reff=0;
do j=1 to Narm[i]-1;
reff=reff+reffwt[reffpt[i],j]randeff[reffind[i]+j];
end;
linpred=alpha[study[i]] + beta[itrt[i]] + reff;
p=1-(1/(1+exp(linpred)));
ll= ll+ r[i]log(p) + (n[i]-r[i])log(1-p);
end;
model general(ll);
/ 标记 2/
LogOR[1]=(beta[2]-beta[1]); B-A;
LogOR[2]=(beta[3]-beta[1]); C-A;
LogOR[3]=(beta[4]-beta[1]); D-A;
LogOR[4]=(beta[3]-beta[2]); C-B;
LogOR[5]=(beta[4]-beta[2]); D-B;
LogOR[6]=(beta[4]-beta[3]); D-C;
OR[1]=exp((beta[2]-beta[1])); B-A;
OR[2]=exp((beta[3]-beta[1])); C-A;
OR[3]=exp((beta[4]-beta[1])); D-A;
OR[4]=exp((beta[3]-beta[2])); C-B;
OR[5]=exp((beta[4]-beta[2])); D-B;
OR[6]=exp((beta[4]-beta[3])); D-C;
ODS output postsummaries=library.post1BIG;
run;
ODS output clear;
参考资料:
[1]META分析软件应用与实例解析 郑明华.pdf
[2]https://baike.baidu.com/item/Meta%E5%88%86%E6%9E%90/4019144?fr=aladdin#ref_[2]_938263
[3]https://mp.weixin.qq.com/s/CSkTWQ99Jn489b96kNYdEw
[4]https://zhuanlan.zhihu.com/p/432971589
[5]https://zhuanlan.zhihu.com/p/405811677

