ABtest 流程

目录
Part 1. A/B Test流程
Part 2. 常见的数据分布
Part 3. 假设检验相关知识
Part 4. 案例分析
Part 5. 总结
版权声明
参考资料

核心结论：

Part 1. A/B Test流程

A/B Test的整体流程可以分为以下几个步骤：
1.设定实验目标
2.确定实验方案
3.A/A 测试
4.显著性检验
5.样本量评估
6.A/B 测试
7.实验效果评估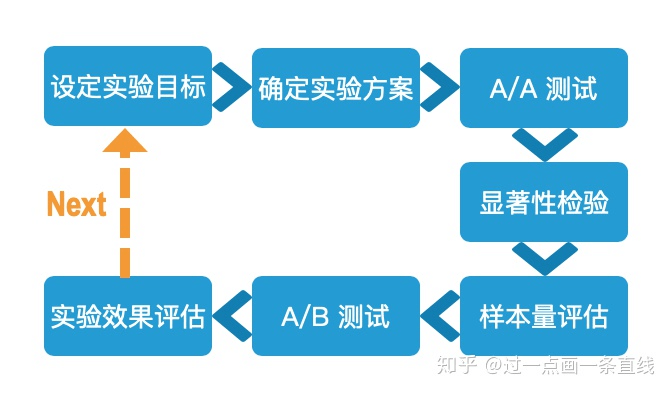

图1. AB Test流程图
1. 设定实验目标
确定我们做AB测试的关注目标，例如转化率、点击率、逾期率等。
2. 确定实验方案
实验方案主要涉及两部分内容，我们的实验组和对照组分别是什么，以及流量如何分配，一般情况下只会有一组实验组和一组对照组（当然也可以同时存在多组实验组）。在信贷业务中，我们往往是用AB测试来验证新策略模型替换旧策略模型的效果，这时候实验组就是新的策略模型，对照组就是旧的策略模型。因为新模型策略的实际线上效果未知，容易造成资损，所以在流量分配上，我们会给与实验组较少的流量，例如10%的流量走新策略模型，90%的流量走旧的策略模型。在广告推荐等业务中，因为反馈快且不容易造成资损，一般会将流量对半分从而快速积累样本从而验证实验组和对照组效果。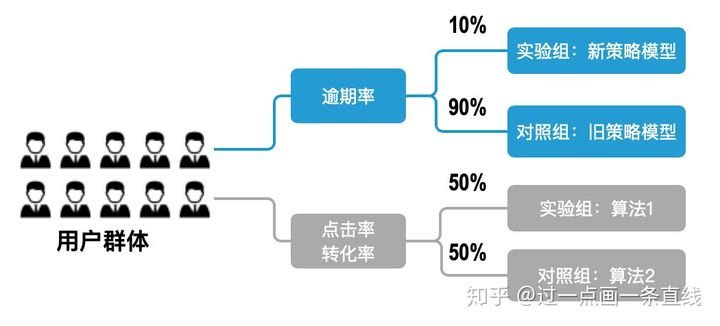

图2. AB Test实验方案
3. A/A 测试
A/A 测试就是我们对实验组和对照组采用同一种测试方案，它被用来检测实验组和对照组是否在统计上的无差异，简单来说就是同一种方案在实验组和对照组上的效果偏差会有多大，该结果也被用来为A/B测试的变化做基线参考。
有时我们在进行A/B测试之前，我们会进行一段时间的A/A测试，来观察两个一样的实验方案在实验组和对照组上的效果变化，把这个变化做为A/B测试的基线。如果A/B测试产生的变化和A/A测试产生的变化相比非常接近，那么A/B测试的结果很可能是随记误差，不具有显著性。同时，A/A测试也可以用来验证在当前样本量下，实验组对照组的分组是否均匀。
理论上来说，对于A/A测试，当样本量足够大时，实验组效果和对照组效果相差无几。所以A/A测试可以有效的检验在一定的样本量下实验组和对照组的样本分布是否一致，减少因分桶的不随机导致的A/B试验结果不准确的可能性。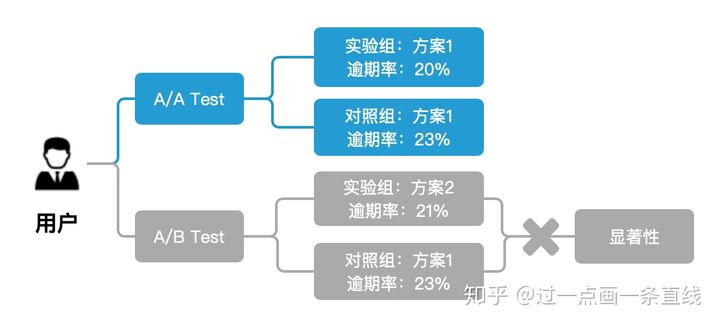

图3. AA Test和AB Test
4. 显著性检验
显著性检验就是事先对总体（随机变量）的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设（备择假设）是否合理，即判断总体的真实情况与原假设是否有显著性差异。 显著性检验是针对我们对总体所做的假设做检验，其原理就是“小概率事件实际不可能性原理”来接受或否定假设。
这里的显著性检验是验证A/A试验的结果是否不存在显著性差异。在A/A试验中，因为我们对实验组和对照组采用了相同的方案，因此只要样本分桶随机的话，两组的实验结果会不存在显著性差异。
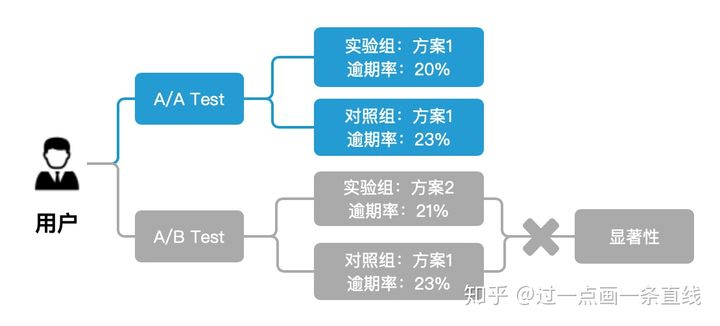
在A/B测试中，我们就是要判断在累计了一定的样本量之后，实验组和对照组之间的差异是否具有显著性。举个例子，如上图3所示，在A/A试验中，当实验组合对照组都累计了5000个样本后，发现都采用方案1的实验组和对照组逾期率分别为20%和23%，逾期率波动为3%。在A/B Test中，积累相同样本后，观察到采用方案2的实验组和采用方案1的对照组逾期率分别为21%和23%。这个时候我们是否能得出方案2优于方案1的结论？通过对比A/A试验的结果，我们可以知道显然不能，A/B测试的结果不具有显著性。

5. 样本量评估
当我们进行A/B试验前或者评估A/B测试的效果时，我们需要进行样本量评估。因为样本量过小则会造成随记结果的引入，试验结果失去统计意义。举个例子，我们对进件用户分为实验组和对照组，在样本量很小的情况下，结果实验组中的新用户远多于对照组，那么实验组中多的新用户会导致逾期率上升，从而带偏整个测试结果。
但是需要强调的是，在A/B测试的过程中不能一昧追求大流量，因为流量过大会增加试错成本，造成大的资损。因此，样本量评估可以很好的预测在多少的样本情况下A/B测试的结果具有显著性。最小样本量的判断可以采用假设实验目标指标符合正态分布下，两类错误发生概率的分位数的方式进行估算，我们将在下面的章节进行介绍。

6. A/B 测试
在进行完上面的步骤后，我们就可以进行A/B测试了。将样本分为实验组和对照组，分别采用不同的方案，从而观察两种方案的差异性。

7. 实验效果评估
实验效果评估主要分为2部分：实验有效性判断、实验结果的比较。
对于实验有效性判断主要包含两部分：1.判断实验的样本量是否已经达到所需的最小样本量，从而能够以较大的概率拒绝两类统计错误的发生。2.判断样本有效性。采用AA测试，如果AA实验的结果不存在显著差异，那么可以认为实验结果是有效的，进而可以对新老版本的实验结果进行进一步的判断。
在确认实验有效后就可以对实验的结果进行判断了，通常通过比较实验组和对照组结果是否存在显著差异（一般通过P值进行判断），以及计算实验结果指标的置信区间（通常选用指标的95%置信区间），从而判断新方案是否相对老方案存在显著提升或下降。

Part 2. 常见的数据分布

在介绍A/B测试的具体数学原理之前我们先来回顾一些常见的数据分布知识。
1. 伯努利分布
在现实生活中很多事件都只有2种结果：抛硬币只有正反面，在新的产品上用户注册或不注册，对于给定的广告用户点击或者不点击等等，这些事件都可以被称作为伯努利实验。
伯努利实验时单次随机试验，只有0和1两种结果，其概率分布称为伯努利分布，也称为0-1分布。我们记事件为1的概率为p，事件为0的概率为(1-p)，简写为 ，其概率质量函数为：

其期望为：

其方差为：

2. 二项分布
在n次独立重复的伯努利试验中，设每次试验中事件A结果为1（发生）的概率为p。用X表示n次伯努利试验中事件A发生的次数，则X的可能取值为0，1，…，n,且对每一个k（0≤k≤n）,事件{X=k}即为“n次试验中事件A恰好发生k次”，随机变量X的离散概率分布即为二项分布，简写为 ：其概率质量函数为：

其中：

其期望为：

其方差为：

一般的二项分布是n次独立的伯努利试验的和，它的期望值和方差分别等于每次单独试验的期望值和方差的和。二项分布期望和方差的具体推导过程参考
薛定谔的月亮：二项分布的均值与方差公式的推导zhuanlan.zhihu.com

3. 泊松分布
泊松分布适合于描述单位时间内随机事件发生的次数，通常用于描述稀有事件（即小概率）事件发生数的分布。现实生活中很多情况是服从泊松分布的：
一天内某个路口发生的交通事故数
单位面积内昆虫的数量
10分钟内到某个ATM机取钱的人数
假设事件{X=k}即为随机事件恰好发生k次，则泊松分布的概率函数为：

其中 是单位时间(或单位面积)内随机事件的平均发生次数.
泊松分布的期望和方差均为 。
4. 正态分布
若随机变量X服从一个数学期望为 、方差为 的正态分布，记为 。其概率密度函数为正态分布的期望值 决定了其位置，其标准差 决定了分布的幅度。当 时的正态分布是标准正态分布。正态分布的概率密度函数为：

5. 中心极限定理
讲完上面这些常见的分布，我们来聊聊中心极限定理，因为在后续的推理过程中我们会用到。
【定理：独立同分布的中心极限定理】 设随机变量X1，X2，……Xn，……独立同分布，并且具有有限的数学期望和方差： ，则对任意x，分布函数

满足

该定理说明，当n很大时，随机变量 近似地服从标准正态分布 。因此，当n很大时， 近似服从正态分布 。该定理是中心极限定理最简单又最常用的一种形式，在实际工作中，只要n足够大，便可以把独立同分布的随机变量之和当作正态变量。
6. 二项分布和泊松分布的关系
对于二项分布来说，当试验的次数趋于无穷大，而乘积np固定时，二项分布收敛于泊松分布。因此参数为λ=np的泊松分布可以作为二项分布B(n,p)的近似，近似成立的前提要求n足够大，而p足够小，np不是很小。
具体证明过程可参考
如何通俗理解泊松分布？数据结构与算法马同学-CSDN博客blog.csdn.net下面我们通过概率密度函数图来看看二者的关系是否如上所说，如图4所示：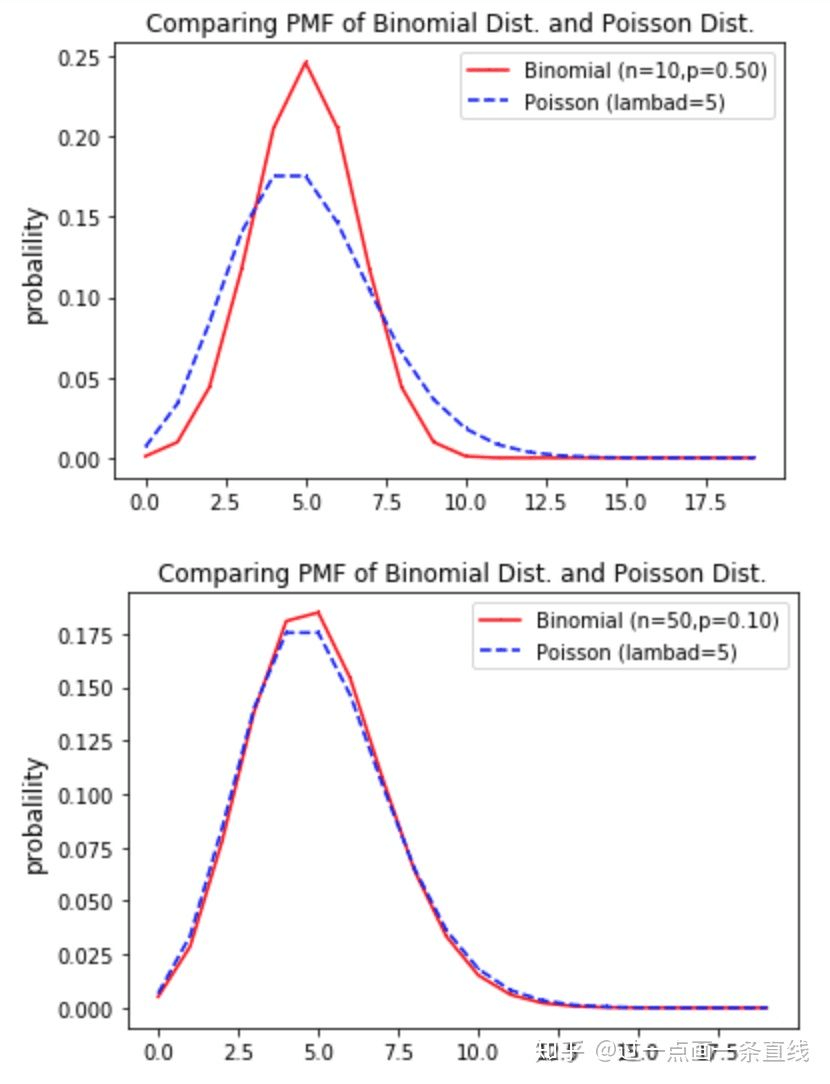

图4. 二项分布和泊松分布概率密度函数
7. 二项分布和正态分布的关系
对于二项分布，如果n足够大，那么分布的偏度就比较小。在这种情况下，如果使用适当的连续性校正，那么 的一个很好的近似是正态分布 ，下面我们通过概率密度函数图来看看二者的关系是否如上所说，如图5所示：

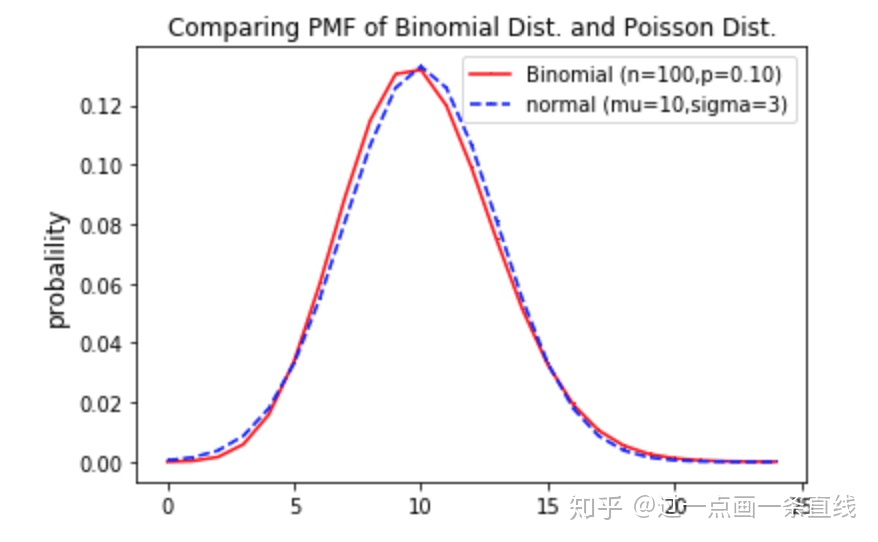
图5. 二项分布和正态分布概率密度函数

Part 3. 假设检验相关知识

下面 要讲的内容是建立在对置信区间、 统计量和 统计量有一定了解的基础上。
1. 假设统计检验和置信区间的关系
置信度和假设检验是紧密相关的，我们通常所做过的假设检验结论都是在给定的置信区间下得出的，改变置信区间的大小得到的结论可能就会发生变化，常用的置信区间为95%。
2. 统计检验的5要素
原假设 ：关于一个或多个总体参数的假设
备择假设 ：如果我们决定拒绝原假设则将接受的假设
检验统计量：由样本数据计算得到
拒绝域：使得原假设被拒绝的检验统计量的取值
结论：做出接受还是拒绝原假设的决定
拒绝为真的原假设是第一类错误，即拒真，犯第一类错误的概率用符号 表示。接受为假的原假设是第二类错误，即纳伪，犯第二类错误的概率用符号 表示。

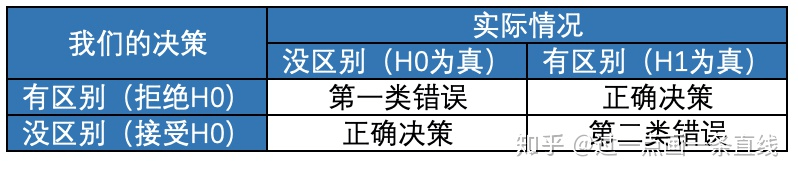
图6. 第一类和第二类错误



从实际含义可知我们希望 越小， 越大，即 越小，也就是犯第一类错误和第二类错误的概率都降低，但实际过程中很难同时做到。
我们都知道，在进行原假设和备择假设的设定时，选择的原则是把希望支持的观点通常作为备择假设，这是为什么呢 ？
这是因为当我们把想要证明的假设作为备择假设时，如果数据支持拒绝 ，我们可以马上得知 的值（置信区间），也就是弃真的概率。如果我们把想要证明的假设作为原假设，而且数据支持该观点，即检验不拒绝 ，那么我们还需要根据备择计算 的值，即纳伪的概率。 的计算往往是一个冗长无味而且有时极度困难的任务（有兴趣的小伙伴可以自己了解一下）。显然，我们希望能回避对 的计算。
3. 案例场景
在实际工作中，我们通常会遇到以下的场景：
【逾期率场景】最近模型团队新开发PD模型，为了验证新模型效果，将人群随机分配进行AB测试，实验组A使用新模型，对照组B使用旧模型。观察了一段时间的结果后，得到如下观测结果：实验组A样本量10000人，逾期量300人；对照组B样本量12000人，逾期量400人。是否能说明在降低逾期率上新模型效果优于旧模型？
为了回答这个问题，我们来介绍下面的知识。
4.检验两个总体比率的差
我们的用户行为服从二项分布 ，其中 为样本量， 为用户的发生点击（转化 或者 逾期）的概率，其中“成功”的次数为 。设样本比率 ，那么它是概率 的一个无偏估计。
根据中心极限定理可知， 近似服从正态分布 。则有：

其中 ，
考虑上面的案例，设 和 分别表示新模型和旧模型的真实逾期率， 和 分别表示实验组和对照组的样本量， 和 分别表示实验组和对照组的逾期样本量。根据实验数据我们得到实验组和对照组的逾期率分别为 和 。 和 分别是 和 的无偏估计， 是 的无偏估计。那么根据上面介绍的我们知道


根据正态分布的性质可知：

下面我们构建 假设的大样本检验
Step1：构建原假设和备择假设
单边检验


双边检验


Step2：构建检验统计量
在两本量足够大的时候， 和 近似服从正态分布，因此差 的抽样分布近似正态。那么如何判断样本量是否足够大，可以通过如下的方法： 的值都大于等于4（根据经验，实际过程中大多数二项总体的样本都是满足该要求的，若不满足则可以构建 检验统计量），此时可以构建检验统计量：

当 时，根据上面的推导可得 标准差为

当 时，即检验 ，此时用联合样本的成功总数除以两个样本总观测值的个数是 的最好估计。此时

在这种情况下， 抽样分布标准差的最好估计可用 代替 和 ，可得

Step3：拒绝域
首先我们会先确定犯第一类错误 的大小，通常取
对于单边检验，拒绝域为 。

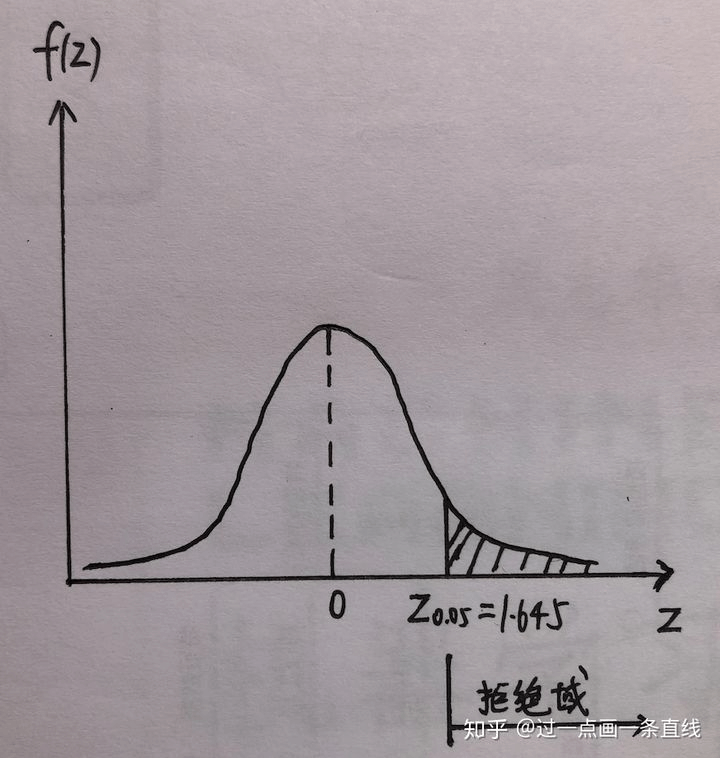
图7. 单边检验拒绝域
对于双边检验，拒绝域为 。

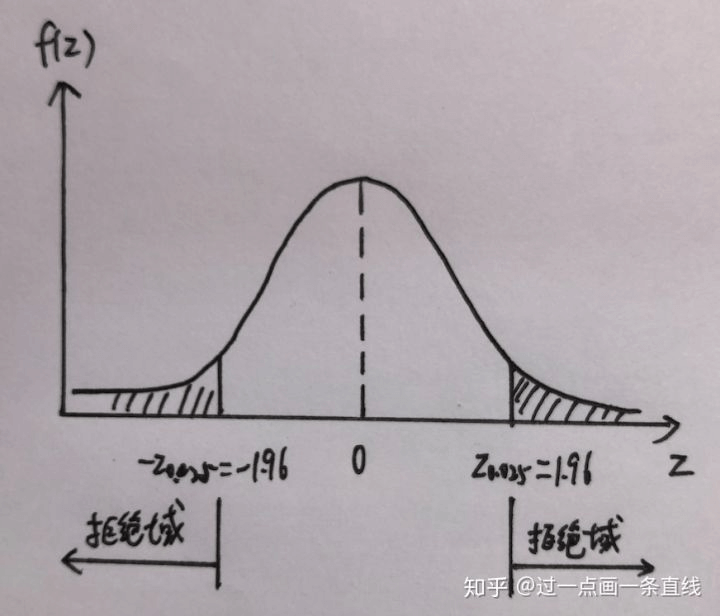
图8. 双边检验拒绝域
通过这种方法，我们要事先给出 值，然后计算相应的拒绝域。但是对于不同的检验人员，能接受的 值大小是不相同的，从而有不同的拒绝域。因此我们给希望给出某个度量值，用该度量值和 比较来决定是拒绝还是接受。这种不一致的度量值称为检验的观测显著性水平（或者p值），当 时，则拒绝原假设，否则则接受原假设。
假设我们计算得到的检验统计量的计算值为 ，那么对于单边检验， ，也就是下图中阴影部分面积。

图9. p值
Step 4. 结论
根据P值和 得出拒绝原假设还是接受原假设的结论
5. 样本量计算
在进行AB实验的过程中，给定对照组基准比率 ，最小提升效果 ，统计显著性 以及统计功效选 ，我们就可以计算达到显著性水平下每组所需的最小实验样本，其计算公式如下:

其中 ，
另外介绍一个计算AB测试样本量的网站
Sample Size Calculatorwww.evanmiller.org至此，假设检验相关的数学知识就介绍完毕了，下面我们对上面的具体案例进行计算。

Part 4. 案例分析

1. 显著性检验
对于前面提到的案例，我们再回顾一下：
【逾期率场景】最近模型团队新开发PD模型，为了验证新模型效果，将人群随机分配进行AB测试，实验组A使用新模型，对照组B使用旧模型。观察了一段时间的结果后，得到如下观测结果：实验组A样本量10000人，逾期量300人；对照组B样本量10000人，逾期量400人。是否能说明在降低逾期率上新模型效果优于旧模型？
Step 1. 构建原假设和备择假设
单边检验


Step2：构建检验统计量

Step3：拒绝域
通过Excel NORMSDIST函数算可得
Step 4. 结论
设定 ，因为P值小于 ，所以拒绝原假设，接受备择假设，认为新模型效果优于旧模型。

2. 样本量计算
【样本量计算场景】假设目前基准转化率20%，目标转化率22%，统计显著性 以及统计功效选 ，那么实验所需的最小样本是多少？
根据上面的公式计算可得 n = 6507
根据上面的AB测试样本量网站计算可得n = 6347
结论：实验组和对照组最小实验样本分别为6507

Part 5. 总结

影响AB测试效果的一个重要影响因素是分桶的随机性，当我们发现实验效果不如意或者过于显著时，也需要去关注实验组和对照组的样本是否是随机分布的（保证两组同分布），是不是因为实验组或者对照组引入了特殊的客群导致的实验效果显著，避免因分桶的不一致性给实验结果带来的干扰。

版权声明

欢迎转载分享，请在文章中注明作者和原文链接，商业转载请联系作者获得授权，非商业转载请注明出处。
原文作者：过一点画一条直线（知乎ID）
知乎专栏：数据化风控
原文链接：https://zhuanlan.zhihu.com/p/144924899

参考资料

[1] Statistics for Engineering and the Sciences