来源:https://zhuanlan.zhihu.com/p/467276292
为什么进行网状meta分析?
在临床实践中,若有一系列的药物可以治疗某种疾病,但RCT均是药物与安慰剂的对照,而药物互相之间的RCT都没有进行或很少,那么在这种情况下,想要进行药物间效应的比较就需要将间接比较和直接比较的证据进行合并,可用的方法为网状Meta分析。
网状meta分析的三个假设前提:
- 同质性假设
此与传统直接比较Meta分析相同,一般用Q统计量检验法,若检验结果无统计学差异,可认为纳入研究具有同质性,采用固定效应模型进行合并;否则需要探讨异质性来源,当无法解释统计学异质性时,采用随机效应模型进行合并,或提示不宜对纳入研究进行合并。 - 相似性假设
包括临床相似性和方法学相似性。临床相似性指AC和BC的两组试验中研究对象、干预措施和结局测量等的相似性,方法学相似性指两组试验的质量相似性。研究表明,若两个试验集足够相似,间接比较可以平衡两个试验集的偏倚,而且相比直接比较偏倚更小。 - 一致性假设
若既有直接比较结果又有间接比较结果,或同时有多个间接比较结果(如:A vs B可以通过AC和BC获得,亦可通过AD和BD获得),在决定是否合并这些结果时,则需要进行第3个水平的一致性检验,如果各比较结果之问差异小的话,认为符合一致假设,可以进行合并;如果出现不一致性,常提示直接比较或问接比较证据存在方法学缺陷,或两者临床特征有差异,或两种原因同时存在,此时需探讨出现不一致性可能的原因并考虑是否应合并直接比较和间接比较证据。R 语 言 实 现
R中的gemtc包可用于网状meta分析。由于gemtc包是基于贝叶斯方法进行的,而rjags包是基于马尔科夫链蒙特卡罗法的软件,是贝叶斯方法的基础,因此首先需要安装JAGS软件:
https://sourceforge.net/projects/mcmc-jags/files/
下面以结局指标为二分类的数据为例,进行R语言实现及结果解读:
第一步:安装并且加载gemtc和rjags包
install.packages(‘gemtc’) install.packages(‘rjags’) library(gemtc) library(rjags)
第二步:读取数据
setwd(“C:\Users\TP\Desktop\Dailyfile”) data <- read.csv(“二分类网状meta分析.csv”, sep=”,”, header=T) treatments <- read.csv(“treatment.csv”, sep=”,”, header=T)
数据格式如下:
data: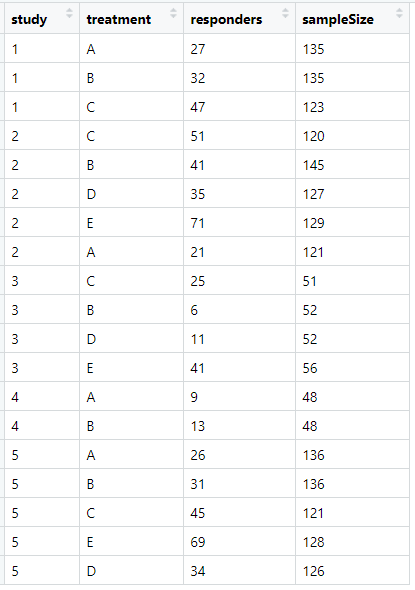
treatments:
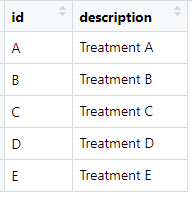
注:结局指标为二分类的数据变量名必须如data数据中所示,不能改变,且干预措施标识也必须如treatments数据中所示。
第三步:画网状关系图
network <- mtc.network(data) plot(network)
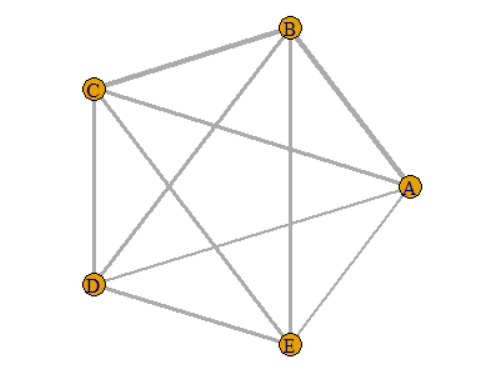
图1 网状关系图
由图1的网状关系图可以看到字母A-E之间均有连线,表示干预措施A-E间均存在直接比较。其中,A与B间的连线比A与E间的粗,可以说明干预措施A与B间直接比较的样本量比A与E间的多。
第四步:建立一致性模型
model <- mtc.model(network, type=”consistency”, n.chain=4, likelihood = “binom”, link=”logit”, linearModel = “random”) results <- mtc.run(model, n.adapt=5000, n.iter = 20000, thin=1) forest(relative.effect(results,”A”))
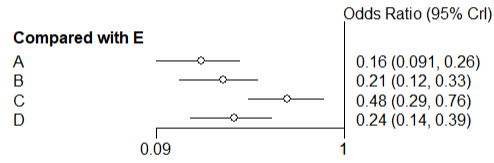
图2 森林图
图2的森林图描述的是干预措施A-D与E之间比较的OR值及95%可信区间(credible intervals,CrI),其中干预措施A与E疗效比较结果的OR值为0.16,表示使用干预措施A结局事件发生的风险是使用干预措施E结局事件发生的风险的0.16倍,OR值的95%可信区间(0.091-0.26)。由于干预措施A-D与E比较的可信区间均没有跨越1,因此它们之间的效应差异均有统计学意义。
(由于篇幅原因,只给出干预措施A-D与E直接的森林图)
第五步:画轨迹图和密度图
plot(results)
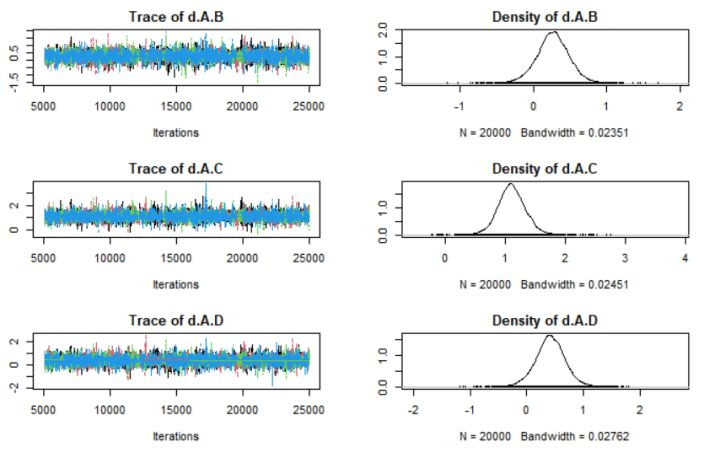
图3 轨迹图和密度图
由图3的轨迹图可知,当迭代次数达到5000次以上时,MCMC链波动稳定并有良好的重叠;由密度图可知,当迭代次数达到20000次时,Bandwith趋向于0并达到稳定,综合说明模型收敛较好。
第六步:画Brooks-Gelman-Rubin诊断图
gelman.plot(results)
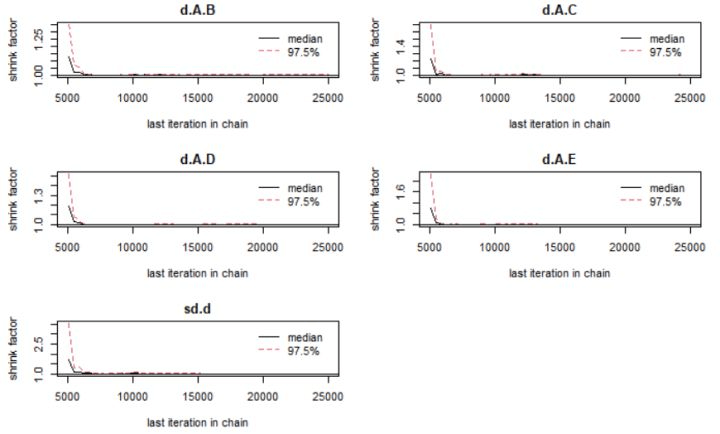
图4 Brooks-Gelman-Rubin诊断图
计算规模缩减因子(potiential scale reduction factor,PSRF)
gelman.diag(results)
表1 PSRF值
| PSRF的点估计 | PSRF 95%置信上限 | |
|---|---|---|
| d.A.B | 1.00 | 1.01 |
| d.A.C | 1.00 | 1.01 |
| d.A.D | 1.00 | 1.00 |
| d.A.E | 1.00 | 1.00 |
| sd.d | 1.00 | 1.00 |
满意的收敛模型需要同时满足3个条件:
(1)缩减因子的中位值经n次迭代计算后趋向于1并达到稳定;
(2)缩减因子的97.5%经n次迭代计算后趋向于1并达到稳定;
(3)PSRF值趋向于1。
由图4和表1可知,模型同时满足上面的收敛的是三个条件,所以是一个满意的收敛模型。
第七步:log(OR)值
relative.effect.table(results)
上面给出的结果为每个干预措施A-E相互比较后取指数对数的结果。
第八步:等级排序
ranks <- rank.probability(results) #单个排序结果 print(ranks)

由单个排序结果可知干预措施E排在第一位的概率为0.9957,排在第五位的概率为0,而干预措施A排在第一位的概率为0,排在第五位的概率为0.8527。
#综合排序结果 sucra(ranks)
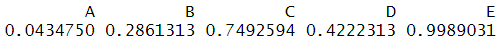
由综合排序结果可知,干预措施E为5种干预措施中最好的,而干预措施A为最差的。
#等级排序图 plot(ranks,beside=TRUE)
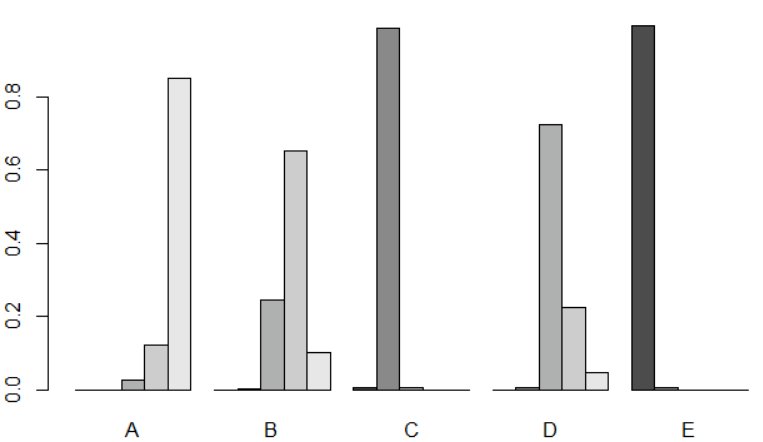
图5 等级排序图
虽然等级排序给出了每个干预措施的排序结果,但是不能简单地下结论说干预措施E为最好的,而干预措施A为最差的,还要结合其他结果综合来看。
第九步:模型局部一致性检验,节点分析法
result.node <- mtc.nodesplit(network, thin=1) summary.ns <- summary(result.node) plot(summary.ns)
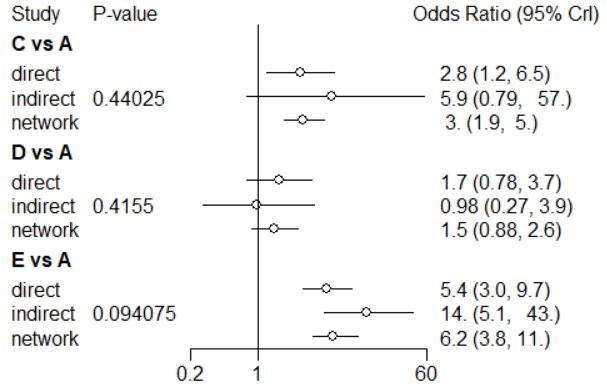
图6 节点分析图
节点分析法是对部分比较结果的一致性进行检验,由节点分析图可知,干预措施C与A、D与A和E与A的直接比较、间接比较和网状比较结果之间P值均大于0.05,没有统计学差异,即一致性较好。
第十步:异质性检验
resultanohe <- mtc.anohe(network, n.adapt=5000, n.iter=20000, thin=1, n.chain=4, likelihood=”binom”, link=”logit”, linearModel=”random”) c <- summary(resultanohe) plot(c)
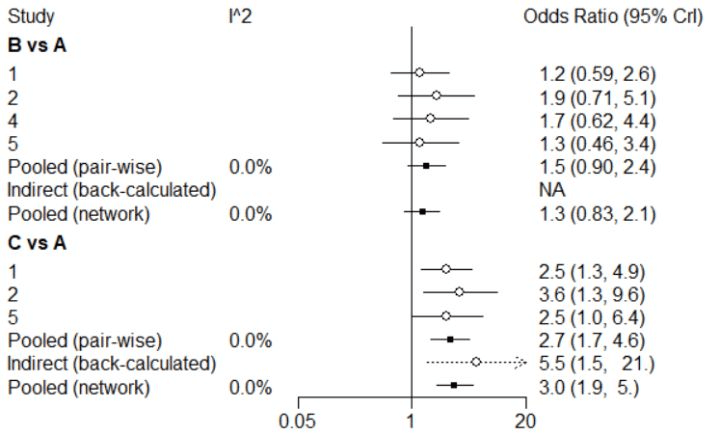
图7 森林图
由图7可知,干预措施B与A的直接比较(pair-wise)之间的I为0%,则它们之间不存在异质性,干预措施B与A的网状比较(network)结果之间的I也为0%,则它们之间满足同质性假设,而干预措施B与A不存在间接比较(back-caculated),所以间接比较为缺失。
(由于篇幅原因,所以只给出其中一张图片)
综合以上结果可知,建立的一致性模型拟合较好,并且满足一致性和同质性假设,除此之外还需要满足相似性假设。就相似性假设而言,目前没有公认的方法来检验,只能通过比较试验特征进行主观判断,或者通过敏感性分析、亚组分析以及Meta回归来识别。这里假设满足相似性假设,最终的结论将从以下几个方面得出:
a. 由图2的森林图可知使用干预措施E与A-D相比,结局事件发生的风险最高;
b. 由第八步等级排序结果可知,干预措施E是排在第一位的;
c. 由第七步log(OR)值的最后一行可知,干预措施A-D与E比较,log(OR)值均小于0,即OR值均小于1,因此使用干预措施E结局事件发生的风险最高。
综合a,b,c可以得出结论:与干预措施A-D相比,使用干预措施E结局事件发生的风险最高。
参考文献:
[1] 张超, 徐畅, 曾宪涛. 网状Meta分析中网状关系图的绘制[J]. 中国循证医学杂志, 2013(11):1382-1386.
[2] 易跃雄, 张蔚, 刘小媛,等. 网状Meta分析图形结果解读[J]. 中国循证医学杂志, 2015(1):103-109.
[3] 张超, 董圣杰, 曾宪涛. R软件gemtc程序包在网状Meta分析中的应用[J]. 中国循证医学杂志, 2013, 13(010):1258-1264.
[4] 曾宪涛, 曹世义, 孙凤,等. Meta分析系列之六:间接比较及网状Meta分析[J]. 中国循证心血管医学杂志, 2012(05):399-402.
[5] Valkenhoef G V , Dias S , Ades A E , et al. Automated generation of node-splitting models for assessment of inconsistency in network meta-analysis[J]. Research Synthesis Methods, 2015, 7(1):80-93.

