高斯混合聚类
    k-means 的结果是每个数据点被 assign 到其中某一个 cluster 了，而 GMM 则给出这些数据点被 assign 到每个 cluster 的概率，又称作 soft assignment
    p(Y|θ)=∑k=1Kakϕ(Y|θk)
    其中
    ϕ(Y|θk)=12π−−√δkexp(−(y−uk)22δ2k)∑k=1Kak=1
    高斯混合模型的意义可以这样理解，以a1,a2,…,aK定义的概率分布从K个高斯分布中选择一个，然后再用这个分布生成一个观测变量yi,这样的过程重复N次，得到观测变量序列Y=y1,y2,…,yN.
    聚类定义
    设样本为X=x1,x2,…,xM ,按照高斯混合模型的定义，这m个样本是由高斯混合模型生成m次得到的，每个样本的生成都由有k个高斯分布组成。如果对于样本j,第k个混合成分的概率为γjk。那么样本j的类标记为
    Cj=argmaxkγjk
    使用EM算法求解高斯混合模型
    1.E步
    Q(θ,θ(i))=∑Zp(Z|Y,θ(i))lnp(Y,Z|θ)
    对于高斯混合模型来说，Y为观测变量，γ为隐变量
    γjk={10如果yj由第k个高斯分布产生
    完全似然函数
    P(Y,γ|θ)=∏j=1Np(yj,γj1,γj2,..,γjK|θ)=∏j=1N∏k=1K(akϕ(yi|θk))γjk=∏k=1Kankk∏j=1Nϕ(yi|θk)γjk
    其中 nk=∑Nj=1γjk,∑Kk=1nk=N
    lnp(Y,γ|θ)=∑k=1K(∑j=1Nγjklnak+∑j=1Nγjk(−0.2ln(2π)−lnδk−(yj−uk)22δ2k))
    Q函数为
    Q(θ,θ(i))=∑k=1K(∑j=1N(∑γjkγjkp(γjk|yj,θ(i)k))lnak+∑j=1N(∑γjkγjkp(γjk|yj,θ(i)k))(−0.2ln(2π)−lnδk−(yj−uk)22δ2k))=∑k=1K(∑j=1Nγjk^lnak+∑j=1Nγjk^(−0.2ln(2π)−lnδk−(yj−uk)22δ2k))

    γjk的期望为
    γjk^=∑γjkγjkp(γjk|yj,θ(i)k)=p(γjk=1|yj,θ(i)k)=p(γjk=1,yj|θ(i)k)∑kk=1p(γjk=1,yj|θ(i)k)=p(yj|γjk=1,θ(i)k)p(γjk=1,|θ(i))∑kk=1p(yj|γjk=1,θ(i)k)p(γjk=1,|θ(i))=akϕ(y|θ(i))∑kk=1akϕ(y|θ(i))
    2.M步
    对uk求导
    ∂Q∂uk=∑j=1Nγjk^yj−ukδ2k=0uk=∑Nj=1γjk^yj∑Nj=1γjk^
    对δk 求导
    ∂Q∂δk=∑k=1Nγjk^(−1δk+δ−3k(yj−uk)2)=0δ2k=∑jj=1γjk^(yj−uk)2∑jj=1γjk^
    对ak求导
    因为 ∑Kk=1ak=1 ， 拉格朗日函数为
    L(a)=Q(θ,θ(i))+λ(∑k=1kak−1)∂L(a)∂ak=∑j=1Nγjk^ak+λ=0ak=−∑Nj=1γjk^λ∑k=1Kak=−∑Kk=1∑Nj=1γjk^λ=1λ=−Nak=∑Nj=1γjk^N
    单高斯分布模型GSM
    多维变量X服从高斯分布时，它的概率密度函数PDF为：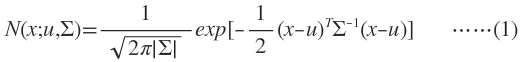
    高斯混合聚类 - 图1
    x是维度为d的列向量，u是模型期望，Σ是模型方差。在实际应用中u通常用样本均值来代替，Σ通常用样本方差来代替。很容易判断一个样x本是否属于类别C。因为每个类别都有自己的u和Σ，把x代入（1）式，当概率大于一定阈值时我们就认为x属于C类。
    从几何上讲，单高斯分布模型在二维空间应该近似于椭圆，在三维空间上近似于椭球。遗憾的是在很多分类问题中，属于同一类别的样本点并不满足“椭圆”分布的特性。这就引入了高斯混合模型。
    高斯混合模型GMM
    GMM认为数据是从几个GSM中生成出来的，即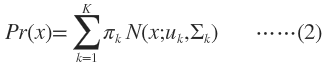
    高斯混合聚类 - 图2
    K需要事先确定好，就像K-means中的K一样。[Math Processing Error]πk是权值因子。其中的任意一个高斯分布N(x;u,Σ)叫作这个模型的一个component。这里有个问题，为什么我们要假设数据是由若干个高斯分布组合而成的，而不假设是其他分布呢？实际上不管是什么分布，只K取得足够大，这个XX Mixture Model就会变得足够复杂，就可以用来逼近任意连续的概率密度分布。只是因为高斯函数具有良好的计算性能，所GMM被广泛地应用。
    GMM是一种聚类算法，每个component就是一个聚类中心。即在只有样本点，不知道样本分类（含有隐含变量）的情况下，计算出模型参数（π，u和Σ）——这显然可以用EM算法来求解。再用训练好的模型去差别样本所属的分类，方法是：step1随机选择K个component中的一个（被选中的概率是[Math Processing Error]πk）；step2把样本代入刚选好的component，判断是否属于这个类别，如果不属于则回到step1。
    样本分类已知情况下的GMM
    当每个样本所属分类已知时，GMM的参数非常好确定，直接利用Maximum Likelihood。设样本容量为N，属于K个分类的样本数量分别是N,N,…,N属于第k个分类的样本集合是L(k)。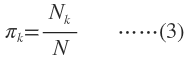
    高斯混合聚类 - 图3
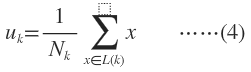
    高斯混合聚类 - 图4
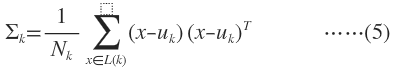
    高斯混合聚类 - 图5
    样本分类未知情况下的GMM
    有N个数据点，服从某种分布Pr(x;θ)，我们想找到一组参数θ，使得生成这些数据点的概率最大，这个概率就是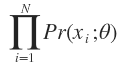
    高斯混合聚类 - 图6
    称为似然函数（Lilelihood Function）。通常单个点的概率很小，连乘之后数据会更小，容易造成浮点数下溢，所以一般取其对数，变成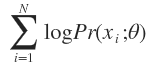
    高斯混合聚类 - 图7
    称为log-likelihood function。
    GMM的log-likelihood function就是：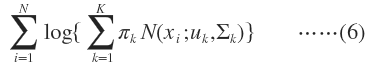
    高斯混合聚类 - 图8
    这里每个样本x所属的类别z是不知道的。Z是隐含变量。
    我们就是要找到最佳的模型参数，使得(6)式所示的期望最大，“期望最大化算法”名字由此而来。
    EM法求解
    EM要求解的问题一般形式是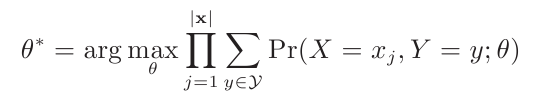高斯混合聚类 - 图9
    Y是隐含变量。
    我们已经知道如果数据点的分类标签Y是已知的，那么求解模型参数直接利用Maximum Likelihood就可以了。EM算法的基本思路是：随机初始化一组参数θ，根据后验概率Pr(Y|X;θ)来更新Y的期望E(Y)，然后用E(Y)代替Y求出新的模型参数θ。如此迭代直到θ趋于稳定。
    E-Step E就是Expectation的意思，就是假设模型参数已知的情况下求隐含变量Z分别取z,z,…的期望，亦即Z分别取z,z,…的概率。在GMM中就是求数据点由各个 component生成的概率。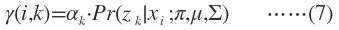
    高斯混合聚类 - 图10
    注意到我们在Z的后验概率前面乘以了一个权值因子α，它表示在训练集中数据点属于类别z的频率，在GMM中它就是π。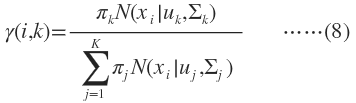
    高斯混合聚类 - 图11
    M-Step M就是Maximization的意思，就是用最大似然的方法求出模型参数。现在我们认为上一步求出的r(i,k)就是“数据点x由component k生成的概率”。根据公式(3),(4),(5)可以推出：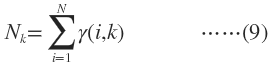
    高斯混合聚类 - 图12
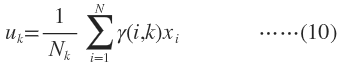
    高斯混合聚类 - 图13
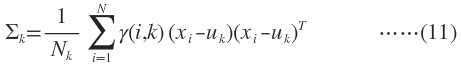
    高斯混合聚类 - 图14
    高斯混合聚类 - 图15
    与K-means比较
    相同点：都是可用于聚类的算法；都需要指定K值。
    不同点：GMM可以给出一个样本属于某类的概率是多少。
    混合高斯模型的原理说白了就一句话：任意形状的概率分布都可以用多个高斯分布函数去近似。换句话说，高斯混合模型（GMM）可以平滑任意形状的概率分布。其参数求解方法一般使用极大似然估计求解，但使用极大似然估计法往往不能获得完整数据（比如样本已知，但样本类别（属于哪个高斯分布）未知），于是出现了EM（最大期望值）求解方法。
    虽然上面说的简单，但是混合高斯模型和EM求解的理论还是比较复杂的，我把我所找到的我认为能够快速掌握高斯混合模型的资料打包到了附件中，大家可以去下载，了解混合高斯模型以及EM的完整推导过程。
    附件下载地址：
    http://download.csdn.net/detail/crzy_sparrow/4187994
    大致抽取下高斯混合模型的重要概念：
    1）任意数据分布可用高斯混合模型（M个单高斯）表示（（1）式）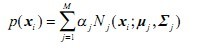
    高斯混合聚类 - 图16（1）
    其中：
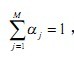    高斯混合聚类 - 图17 （2）
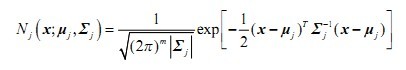    高斯混合聚类 - 图18 （3） 表示第j个高斯混合模型
    2）N个样本集X的log似然函数如下：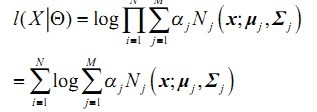
    高斯混合聚类 - 图19 （4）
    其中：
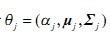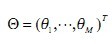    参数：高斯混合聚类 - 图20，高斯混合聚类 - 图21 （5）
    下面具体讲讲基于EM迭代的混合高斯模型参数求解算法流程：
    1）初始参数由k-means（其实也是一种特殊的高斯混合模型）决定：
    [plain] view plain copy

    1. function [Priors, Mu, Sigma] = EM_init_kmeans(Data, nbStates)
    2. % Inputs ————————————————————————————————-
    3. % o Data: D x N array representing N datapoints of D dimensions.
    4. % o nbStates: Number K of GMM components.
    5. % Outputs ————————————————————————————————
    6. % o Priors: 1 x K array representing the prior probabilities of the
    7. % K GMM components.
    8. % o Mu: D x K array representing the centers of the K GMM components.
    9. % o Sigma: D x D x K array representing the covariance matrices of the
    10. % K GMM components.
    11. % Comments ———————————————————————————————-
    12. % o This function uses the ‘kmeans’ function from the MATLAB Statistics
    13. % toolbox. If you are using a version of the ‘netlab’ toolbox that also
    14. % uses a function named ‘kmeans’, please rename the netlab function to
    15. % ‘kmeans_netlab.m’ to avoid conflicts.
    17. [nbVar, nbData] = size(Data);
    19. %Use of the ‘kmeans’ function from the MATLAB Statistics toolbox
    20. [Data_id, Centers] = kmeans(Data’, nbStates);
    21. Mu = Centers’;
    22. for i=1:nbStates
    23. idtmp = find(Data_id==i);
    24. Priors(i) = length(idtmp);
    25. Sigma(:,:,i) = cov([Data(:,idtmp) Data(:,idtmp)]’);
    26. %Add a tiny variance to avoid numerical instability
    27. Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
    28. end
    29. Priors = Priors ./ sum(Priors);

    2）E步（求期望）
    求取：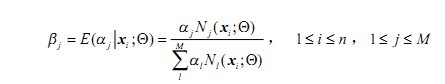
    高斯混合聚类 - 图22（7）
    其实，这里最贴切的式子应该是log似然函数的期望表达式
    事实上，3）中参数的求取也是用log似然函数的期望表达式求偏导等于0解得的简化后的式子，而这些式子至于（7）式有关，于是E步可以只求（7）式，以此简化计算，不需要每次都求偏导了。
    [plain] view plain copy

    1. %% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    2. for i=1:nbStates
    3. %Compute probability p(x|i)
    4. Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));
    5. end
    6. %Compute posterior probability p(i|x)
    7. Pix_tmp = repmat(Priors,[nbData 1]).*Pxi;
    8. Pix = Pix_tmp ./ repmat(sum(Pix_tmp,2),[1 nbStates]);
    9. %Compute cumulated posterior probability
    10. E = sum(Pix);

    [plain] view plain copy

    1. function prob = gaussPDF(Data, Mu, Sigma)
    2. % Inputs ————————————————————————————————-
    3. % o Data: D x N array representing N datapoints of D dimensions.
    4. % o Mu: D x K array representing the centers of the K GMM components.
    5. % o Sigma: D x D x K array representing the covariance matrices of the
    6. % K GMM components.
    7. % Outputs ————————————————————————————————
    8. % o prob: 1 x N array representing the probabilities for the
    9. % N datapoints.
    11. [nbVar,nbData] = size(Data);
    13. Data = Data’ - repmat(Mu’,nbData,1);
    14. prob = sum((Datainv(Sigma)).Data, 2);
    15. prob = exp(-0.5prob) / sqrt((2pi)^nbVar * (abs(det(Sigma))+realmin));

    3）M步（最大化步骤）
    更新权值：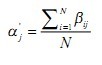
    高斯混合聚类 - 图23
    更新均值：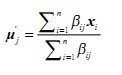
    高斯混合聚类 - 图24
    更新方差矩阵：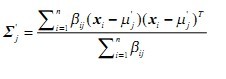
    高斯混合聚类 - 图25
    [cpp] view plain copy

    1. %% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    2. for i=1:nbStates
    3. %Update the priors
    4. Priors(i) = E(i) / nbData;
    5. %Update the centers
    6. Mu(:,i) = Data*Pix(:,i) / E(i);
    7. %Update the covariance matrices
    8. Data_tmp1 = Data - repmat(Mu(:,i),1,nbData);
    9. Sigma(:,:,i) = (repmat(Pix(:,i)’,nbVar, 1) . Data_tmp1Data_tmp1’) / E(i);
    10. %% Add a tiny variance to avoid numerical instability
    11. Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
    12. end

    4）截止条件
    不断迭代EM步骤，更新参数，直到似然函数前后差值小于一个阈值，或者参数前后之间的差（一般选择欧式距离）小于某个阈值，终止迭代，这里选择前者。附上结合EM步骤的代码：
    [cpp] view plain copy

    1. while 1
    2. %% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    3. for i=1:nbStates
    4. %Compute probability p(x|i)
    5. Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));
    6. end
    7. %Compute posterior probability p(i|x)
    8. Pix_tmp = repmat(Priors,[nbData 1]).*Pxi;
    9. Pix = Pix_tmp ./ repmat(sum(Pix_tmp,2),[1 nbStates]);
    10. %Compute cumulated posterior probability
    11. E = sum(Pix);
    12. %% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    13. for i=1:nbStates
    14. %Update the priors
    15. Priors(i) = E(i) / nbData;
    16. %Update the centers
    17. Mu(:,i) = Data*Pix(:,i) / E(i);
    18. %Update the covariance matrices
    19. Data_tmp1 = Data - repmat(Mu(:,i),1,nbData);
    20. Sigma(:,:,i) = (repmat(Pix(:,i)’,nbVar, 1) . Data_tmp1Data_tmp1’) / E(i);
    21. %% Add a tiny variance to avoid numerical instability
    22. Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
    23. end
    24. %% Stopping criterion %%%%%%%%%%%%%%%%%%%%
    25. for i=1:nbStates
    26. %Compute the new probability p(x|i)
    27. Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));
    28. end
    29. %Compute the log likelihood
    30. F = Pxi*Priors’;
    31. F(find(F<realmin)) = realmin;
    32. loglik = mean(log(F));
    33. %Stop the process depending on the increase of the log likelihood
    34. if abs((loglik/loglik_old)-1) < loglik_threshold
    35. break;
    36. end
    37. loglik_old = loglik;
    38. nbStep = nbStep+1;
    39. end

    结果测试（第一幅为样本点集，第二幅表示求取的高斯混合模型，第三幅为回归模型）：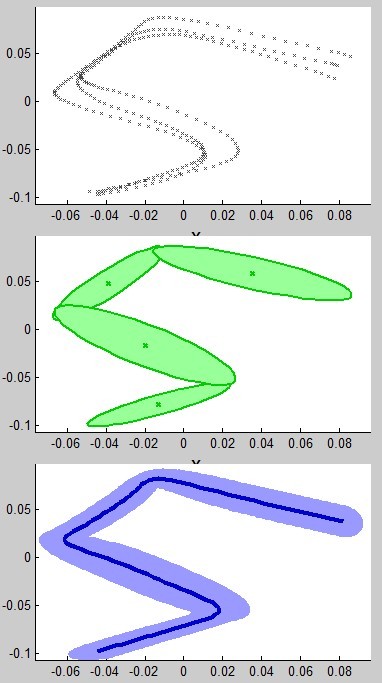
    高斯混合聚类 - 图26
    忘了说了，传统的GMM和k-means一样，需要给定K值（即:要有几个高斯函数）。
    高斯混合模型代码实现流程：
    （1）·首先是初始化，高斯混合模型的效果很大程度上依赖于初始点的设定。一般我们用K-means聚类生成K个中心节点。对于属于同一节点的数据，我们求其均值，方差以及该节点的概率。这里所谓的均值就是中心节点，协方差矩阵按照定义求解，该节点概率（选择该个高斯模型的概率）= 属于该节点的数据个数 / 总数据个数，这样初始化完成。
    （2）·E-STEP:求得Q(j)，这里要将上次得到的均值u，协方差sigma，模型概率pj，带入Q(j)的定义式（见“高斯混合模型之理解”），注意p(x|j)是j类高斯概率分布；
    （3）·M-STEP:按照我们推导的公式，更新均值u，协方差sigma和模型概率pj；
    （4）·将（3）中更新的参数带入（2）中更新Q(j)；
    （5）·最后要设定阀值，使迭代结束。按照定义，我们要将u,sigma,pj，带入L(theta)（最大似然值）公式中，如果t+1时刻的L与t时刻的L的比值接近于1，即可停止。具体的阀值还要应对实际的数据进行调整；
    我的代码（MATLAB）：
    ·初始化函数：
    [cpp] view plain copy
    print?

    1. function [ mu,m_sigma,mp ] = GMM_ini( data,n_center )
    4. [m,n]=size(data);
    5. [data_id,centers]=kmeans(data,n_center);
    6. mu=centers;
    7. mp=zeros(1,n_center);
    8. m_sigma=zeros(n,n,n_center);
    11. for i=1:n_center
    12. tem_id=(data_id==i);
    13. m_sigma(:,:,i)=sigma(data(tem_id,:));
    14. mp(i)=sum(tem_id)/m;
    15. end
    17. end

    [cpp] view plain copy
    print?

    1. function sig=sigma(data)//计算初始化的方差
    4. [m,n]=size(data);
    5. u=mean(data,1);
    6. tem_data=data-repmat(u,m,1);
    9. sig=zeros(n,n);
    10. for k1=1:m
    11. % for k2=1:m
    12. sig=sig+tem_data(k1,:)’*tem_data(k1,:);
    13. % end
    14. end
    15. sig=(sig+ 1E-5.*diag(ones(n,1)))/m;
    16. end

    ·高斯概率分布函数
    [cpp] view plain copy
    print?

    1. function gp=GaussianPDF(data,u,sigma)
    3. [m,n]=size(data);
    5. pre_item=1/sqrt(((2pi)^n)abs(det(sigma)+realmin));
    6. nxt_item(1:m)=0;
    7. tem_data=data-repmat(u,m,1);
    8. for i=1:m
    9. tem_data_t=tem_data(i,:)’;
    10. nxt_item(i)=exp(-0.5(tem_data(i,:)(inv(sigma))*tem_data_t));
    11. end
    13. gp=pre_item*nxt_item;
    15. end


    ·EM算法函数
    [cpp] view plain copy
    print?

    1. function [mu,msigma,mp]=GMM(data,n_center,loglik_threshold)
    3. [ mu,msigma,mp ] = GMM_ini( data,n_center );
    4. disp(‘GMM_Ini Completed ! ‘);
    6. Qt=E_step(data,mu,msigma,mp);
    7. loglik_pre=loglike(data,mu,msigma,mp);
    8. step=0;
    10. while 1
    11. [mu,msigma,mp]=M_step(Qt,data);
    12. loglik_nxt=loglike(data,mu,msigma,mp);
    13. if abs((loglik_nxt/loglik_pre)-1) < loglik_threshold
    14. break;
    15. end
    17. if step>4
    18. break;
    19. end
    21. step=step+1;
    22. step
    23. loglik_pre=loglik_nxt;
    24. Qt=E_step(data,mu,msigma,mp);
    27. end
    29. end
    31. function Qt=E_step(data,mu,m_sigma,mp)//E_STEP
    33. n_model=length(mp);
    34. m=size(data,1);
    35. pxj(m,n_model)=0;
    37. for j=1:n_model
    38. pxj(:,j)=GaussianPDF(data,mu(j,:),m_sigma(:,:,j));
    39. end
    41. px=pxj.*repmat(mp,m,1);
    42. sp=sum(px,2);
    43. Qt=px./repmat(sp,1,n_model);
    45. end
    47. function [lu,lsigma,lp]=M_step(Qt,data)//M_STEP
    49. [m,n_model]=size(Qt);
    50. n=size(data,2);
    52. lu=zeros(n_model,n);
    53. lsigma=zeros(n,n,n_model);
    54. lp=zeros(1,n_model);
    56. mul_data=zeros(n,n);
    58. for j=1:n_model
    59. lu(j,:)=sum(data.*repmat(Qt(:,j),1,n))/sum(Qt(:,j));
    60. tem_data=data-repmat(lu(j,:),m,1);
    61. for k=1:m
    62. mul_data=mul_data+tem_data(k,:)’tem_data(k,:)Qt(k,j);
    63. end
    64. lsigma(:,:,j)=realmin+mul_data/sum(Qt(:,j));
    65. lp(j)=sum(Qt(:,j))/m;
    66. end
    69. end
    71. function loglik=loglike(data,mu,msigma,mp)//似然值
    73. n_center=size(mu,1);
    74. pxj=zeros(size(data,1),n_center);
    75. for j=1:n_center
    76. pxj(:,j) = GaussianPDF(data, mu(j,:), msigma(:,:,j));
    77. end
    78. F = pxj*mp’;
    79. F(F<realmin) = realmin;
    80. loglik = log(sum(F));
    82. end


    ·测试函数
    [cpp] view plain copy
    print?

    1. clear all;
    2. clc;
    3. data=rand(1000,128);//1000个128维的数据样本
    4. n_center=4;
    5. thresh=0.0005;
    6. [u,sigma,p]=GMM(data,n_center,thresh);
    8. disp(‘Test Completed !’);

    注意，模型数在3-5左右，阀值要在0.0005-0.001，否则容易得到奇异方差矩阵。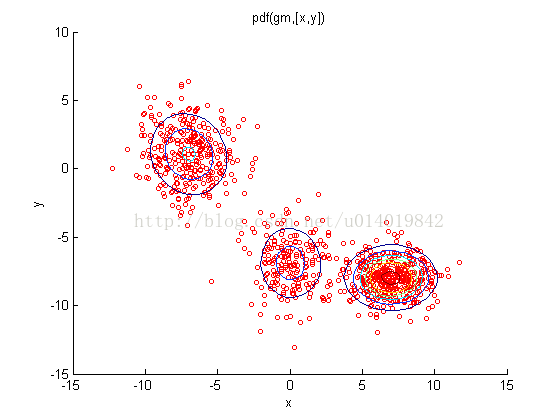
    高斯混合聚类 - 图27
    %% 导入数据
    load(‘kmeansdata’)
    %% 初始化混合模型参数
    K = 3;
    % 随机初始化均值和协方差
    means = randn(K,2);
    for k = 1:K
    covs(:,:,k) = rand_eye(2);
    end
    priors = repmat(1/K,1,K); % 初始化，假设隐含变量服从先验均匀分布
    %% 主算法
    MaxIts = 100; % 最大迭代次数
    N = size(X,1); % 样本数
    q = zeros(N,K); % 后验概率
    D = size(X,2); % 维数
    cols = {‘r’,’g’,’b’};
    plotpoints = [1:1:10,12:2:30 40 50];
    B(1) = -inf;
    converged = 0;
    it = 0;
    tol = 1e-2;
    while 1
    it = it + 1;
    % 把乘除化为对数加减运算，防止乘积结果过于接近于0
    for k = 1:K
    const = -(D/2)_log(2_pi) - 0.5_log(det(covs(:,:,k)));
    Xm = X - repmat(means(k,:),N,1);
    temp(:,k) = const - 0.5 diag(Xm_inv(covs(:,:,k))_Xm’); end
    % 计算似然下界
    if it > 1
    B(it) = sum(sum(q._log(repmat(priors,N,1))))+ sum(sum(q._temp)) - sum(sum(q.    log(q)));
    if abs(B(it)-B(it-1))converged = 1;
    end
    end
    if converged == 1 || it > MaxIts
    break
    end
    % 计算每个样本属于第k类的后验概率
    temp = temp + repmat(priors,N,1);
    q = exp(temp - repmat(max(temp,[],2),1,K));
    q(q < 1e-60) = 1e-60;
    q(q > (1-(1e-60))) = 1-(1e-60);
    q = q./repmat(sum(q,2),1,K); % 更新先验分布
    priors = mean(q,1); % 更新均值
    for k = 1:K
    means(k,:) = sum(X._repmat(q(:,k),1,D),1)./sum(q(:,k)); end
    % 更新方差
    for k = 1:K
    Xm = X - repmat(means(k,:),N,1);
    covs(:,:,k) = (Xm._repmat(q(:,k),1,D))’*Xm;
    covs(:,:,k) = covs(:,:,k)./sum(q(:,k));
    end
    end
    %% plot the data
    figure(1);hold on;
    plot(X(:,1),X(:,2),’ko’)
    ;for k = 1:K
    plot_2D_gauss(means(k,:),covs(:,:,k), -2:0.1:5,-6:0.1:6);
    end
    ti = sprintf(‘After %g iterations’,it);
    title(ti)
    %% 绘制似然下界迭代过程图
    figure(2);
    hold off
    plot(2:length(B),B(2:end),’k’);
    xlabel(‘Iterations’);
    ylabel(‘Bound’);
    ‘