提升指数越大,模型的运行效果越好
上一讲,我们分析了混淆矩阵。今天,我们讲什么是提升图,什么是洛伦兹曲线。
首先,让我们先忘掉这些术语,看看问题的本质是什么。
我们先借用一下上一讲的两张图,来看看有了混淆矩阵,为啥还要搞个“提升图”与洛伦兹曲线出来。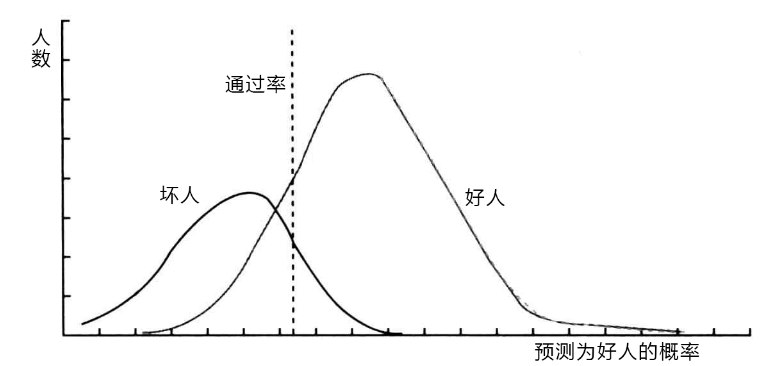
图 1 好人与坏人在预测概率区间上的分布
图1展示的,是一个风控模型预测的概率与“好人”和“坏人”人数的分布关系
现在的问题是,我们有几个风控模型的时候,就会产生很多个像图1一样的分布图,这些模型的优劣该怎么对比呢?
我们先从具体的例子谈。假设我们有10000笔借款,发生了700笔坏账。那么如果我们把这10000笔借款随机分成10等份,那每等份(1000笔)的坏账应该在70笔。也就是说,这些坏账是均匀分布的。
好的,现在我们有模型了,通过模型我们给每个贷款都评估出了一个是好人的概率(吐槽一下,《信用风险评分卡》书中的模型,一会儿预测的是“好人”的概率,一会儿是“坏人”的概率,容易绕晕了)。然后这10000笔贷款可以按照这个概率排序了,从低到高(注意,值越低的是坏人,高的是好人)来排,排名越靠前的,是坏人的概率越高。我们从前往后将序列也分成10等份。那么应该是,越靠前的等份里,包含的坏人应该越多,越靠后的等份里,包含的坏人要更少(好人更多)。一个理想的模型,应该是这个排序与真实的排序是一样的,即,从一个分割点开始,靠前的都是坏人,靠后的都是好人。
很可惜,这个模型只有上帝能做出来,我们人做的模型会误杀好人,也会漏掉坏人。对这个概率来讲,也就是说,有些好人,可能模型算出来的违约概率比较高,而有些坏人,可能模型算出来的违约概率比较低。
我们能做的,就是尽量将越多的坏人排到前面越好。
在《信用风险评分卡》研究一书中,给出了一个具体的例子来讲解这个问题。在此我们引用过来看一下,我会尽量将术语用白话来表达,并且纠正该书中文版本中的错误(书是好书,英文原版没看到,中文版里各种小问题一大堆),以便大家理解。
例1 我们用逻辑回归做了一个模型A,用一个总量为10000,违约率为7%,即违约记录为700个的样本进行模型测试。我们用A给这10000个人评估出好人的概率,将这些记录按照概率的升序进行排列,并分为10等份,如表1所示。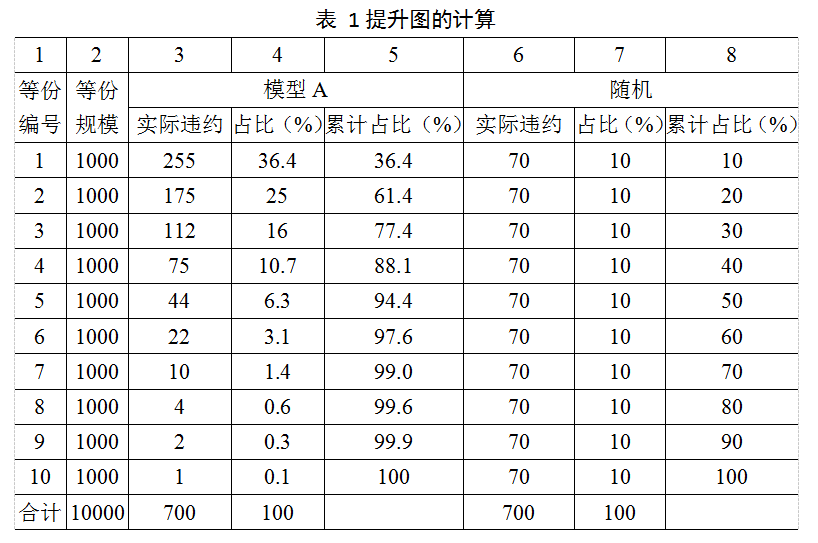
为了对比起见,6到8列将本篇开始提到的随机分成10等份的情况也列了出来。第3列表示每个等份中对应的实际违约的数量;第4列表示这个数量占总违约数的比例(简称占比);第5列是将这个占比累计起来的值,物理含义是,前多少个等份中包含的违约数量占总违约量的比例。
我们将两种方法的每份违约占比(第4列与第7列)放到一张柱状图上(如图2所示),就能形成一个清晰的比较,这张图就叫做提升图。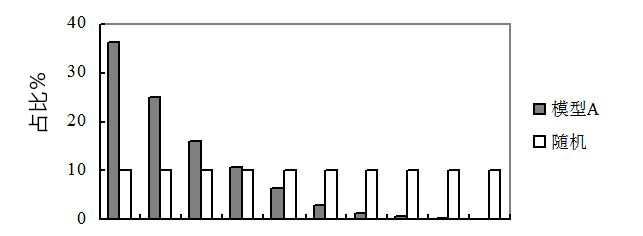
图2 提升图
提升图可以直观的看出一个模型有没有问题。
图3给出一个例子,我们发现,每一等份的占比不是递减的,第3等份反而比第4等份的要少,第7等份比第8等份要少,这种模型被认为是“不一致”的,一般这样的模型被认为是不可用的,需要重新开发模型。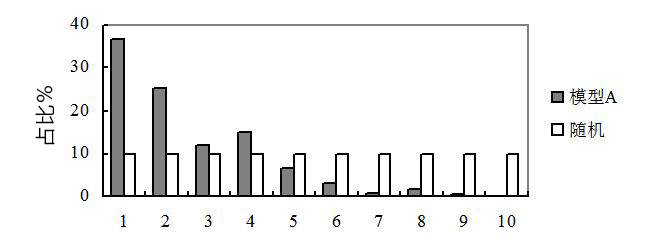
图 3 不一致模型的提升图
我们将两种方法的累计占比(第5列与第8列)放到一张曲线图上(如图4所示),也能形成一个清晰的比较,这张图就叫做洛伦兹曲线。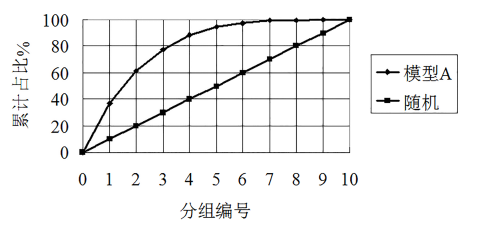
图 4 洛伦兹曲线(虚线的位置为4那一列竖线)
洛伦兹曲线可以直观的衡量两个模型的优劣。如图5所示,A模型要比B模型好,因为任意给一个审批通过率(比如,虚线位置所示,拒绝率40%,意味着60%的通过率,模型A将能识别出88%的违约账户,而模型B只能分离出78%的违约账 模型B那条线未画出来 就是4那条线对上去)。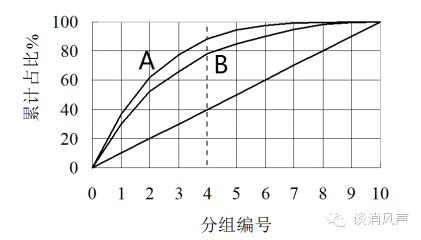
图 5 洛伦兹曲线比较两个模型
总结一下,从提升图上来看,柱状图应该是(单调)递减的,而从洛伦兹曲线上来看,越“往左上角鼓”的,模型的效果是越好的。
讲明白了洛伦兹曲线的意义,有读者肯定好奇洛伦兹是谁。这哥们是个统计学家,名字叫做Max Otto Lorenz,他在1907年为了研究国民收入在国民之间的分配问题,提出了著名的洛伦兹曲线。感叹一下,这哥们肉体1959年就挂了,但是其精神,到现在仍然指导着我们的技术发展,却是个大牛。
/*
Credit Risk Scorecards: Development and Implementation using SAS
(c) Mamdouh Refaat
**/
/*/
/ Macro LiftChart /
/*/
%macro LiftChart(DSin, ProbVar, DVVar, DSLift,mlift);
/ Calculation of the Lift chart data from
the predicted probabilities DSin using
the PorbVar and DVVar. The lift chart data
is stored in DSLift. We use 10 deciles.
/
/ Sort the observations using the predicted Probability in descending order/
proc sort data=&DsIn;
by descending &ProbVar;
run;
/ Find the total number of Positives /
%local P Ntot;
proc sql noprint;
select sum(&DVVar) into:P from &DSin;
select count() into: Ntot from &DSin;
quit;
%let N=%eval(&Ntot-&P); / total Negative(Good) /
/ Get Count number of correct defaults per decile /
data &DSLift;
set &DsIn nobs=nn ;
by descending &ProbVar;
retain Tile 1 SumP 0 TotP 0 SumN 0 TotN 0;
Tile_size=ceil(NN/10);
TilePer=Tile/10;
label TilePer =’Percent of Population’;
label TileP=’Percent of population’;
if &DVVar=1 then SumP=SumP+&DVVar;
else SumN=SumN+1;
PPer=SumP/&P; / Positive % /
NPer=SumN/&N; / Negative % */
label PPer=’Percent of Positives’;
label NPer=’Percent of Negatives’;
if _N = TileTile_Size then do;
output;
if Tile <10 then Tile=Tile+1;
end;
keep TilePer PPer NPer;
run;
/ Add the zero value to the curve /
data temp;
TilePer=0;
PPer=0;
NPer=0;
run;
Data &DSLift;
set temp &DSlift;
lift=pPer-nPer;
run;
symbol1 value=dot color=red interpol=join height=1;
legend1 position=top;
symbol2 value=dot color=blue interpol=join height=1;
symbol3 value=dot color=green interpol=join height=1;
proc gplot data=&DSLIFT;
plot( PPer nper)TILEper / overlay legend=legend1;
run;
quit;
goptions reset=all;
proc sql ;
select max(lift) into :&Mlift from &DSlift;
quit;
%mend;
%let Dsin=sas_2017.m1;
%let ProbVar=pred_runoff_flag;
%let DVVar=runoff_flag;
%**_LiftChart**(&DSin,&ProbVar, &DVVar,DSLift,M_lift);

