来源：https://blog.csdn.net/baidu_39413110/article/details/106362118

不论是开发逻辑回归评分卡，还是GBM机器学习模型，变量的相关性分析和筛选都是必不可少的一步，因为这个过程会帮助我们优化模型结构、丰富模型维度、增强模型鲁棒性，也可以帮助我们在建模开始前对所有变量的维度有个整体的把握。本篇介绍的是对Applied Predictive Modeling一书中的变量相关性分析方法的实践操作。

一、变量相关性分析

变量相关性分析这里使用了pyecharts中的热力图对变量相关矩阵进行了一个展现，但为了更方便我们整体把握所有变量的相关维度，这里先使用Kmeans对所有变量进行了一个聚类（不同于常规使用Kmeans时对样本进行聚类，这里是对特征进行聚类，目的是把高相关的变量分到一类中），根据聚类结果对变量进行了排序，然后计算相关矩阵并展示，这样可以达到的效果就是相互之间高相关的变量都会被排在一起，在图中我们就可以根据高相关区块去很容易发现哪些变量之前同质性很强，而且整个变量池中大概有几个高相关区块（如图）。

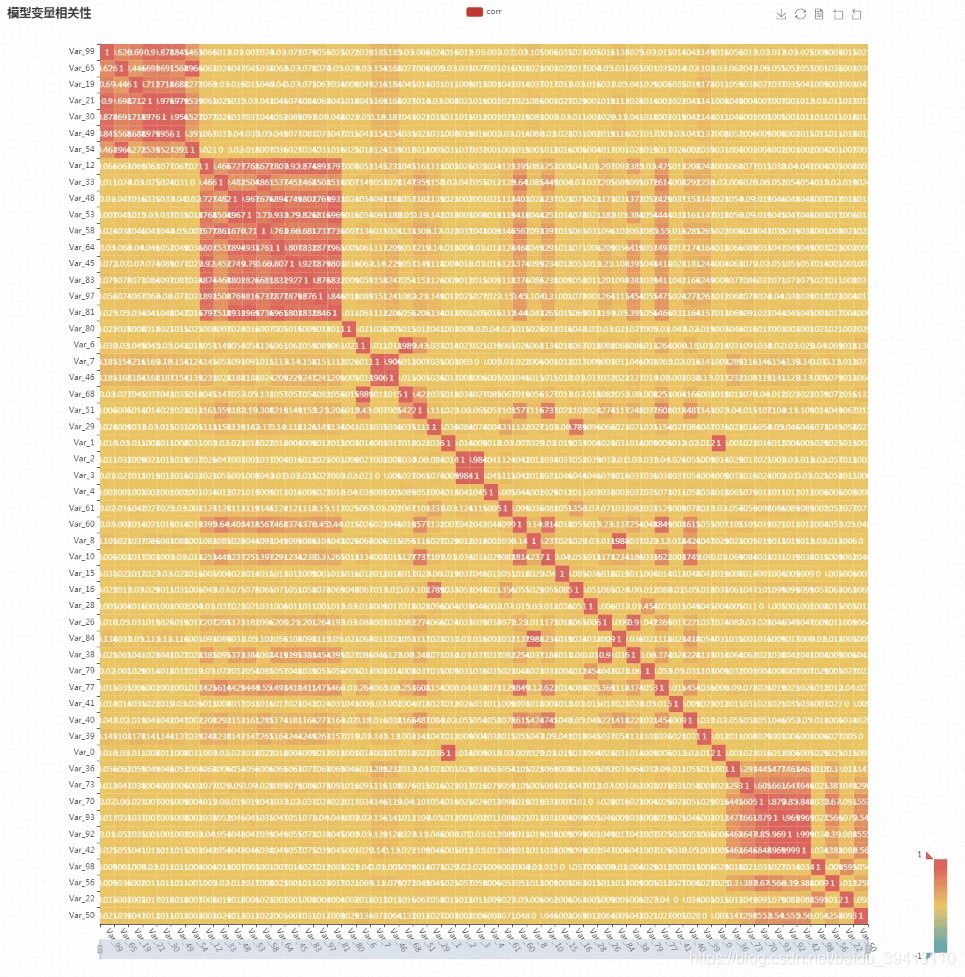
image.png

二、变量相关性筛选

变量相关性剔除方法有很多，业务实操中主要使用的方法有这么几种：

相关性高的两个变量，随便删除一个，保留一个；这种方法显然看着就不严谨不科学；
相关性高的两个变量，删除缺失率高的那个变量；相比第一种方法有进步，但根据缺失率这个指标删变量，不一定对最后的模型效果有改善；
相关性高的两个变量，删除IV值低的那个；这个方法合理，但是耗时，尤其是在变量池很大的时候，需要先对每个变量分箱计算IV。我们更希望的是相关性处理放在IV值筛选之前，这样可以大大减少我们需要计算IV值的变量数，从而优化特征处理过程；
相关性高的两个变量，删除GBM模型重要性低的那个；弊端同上；

相关性高的两个变量，删除和其它变量整体相关更高的那个，这个方法就是我们今天要介绍的，其目的就是在一定的相关阈值之下，尽量多地保留变量，其具体算法过程如下：
计算所有变量的相关矩阵；

  1. 挑选出相关系数最高的一对变量A和B；
  2. 分别对A和B计算其与其它变量相关系数的平均值α \alphaα，β \betaβ；
  3. 如果α > β \alpha>\betaα>β，删除变量A，否则删除B。
  4. 重复2-4步直到所有变量两两之间的相关系数低于给定阈值。

    三、代码实现

    ```python import pandas as pd import numpy as np from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler from pyecharts.charts import HeatMap import pyecharts.options as opts from copy import copy

class cal_corr:

  1. def __init__(self, df, n_clusters=5, threshold=0.7):
  2.     #对所有变量矩阵先进行处理
  3.     self.df = self.handle_df(df.copy())
  4.     #Kmeans聚类的时候指定聚成几类
  5.     self.n_clusters = n_clusters
  6.     #相关性筛选时的阈值
  7.     self.threshold = threshold
  8.     #变量的相关矩阵存下来
  9.     self.corr = None
  11. @property
  12. def corr_matrix(self):
  13.     #变量的相关矩阵
  14.     return self.corr
  16. @property
  17. def corr_pairs(self):
  18.     #变量两两间的相关系数对
  19.     return self.pairs
  22. def handle_df(self,df):
  23.     '''
  24.     先处理一下变量矩阵：
  25.     类别型变量做编码处理
  26.     缺失值填充为中位数
  27.     所有变量做一下均一化处理
  28.     '''
  30.     for item in df.select_dtypes(include=["object"]):
  31.         df[item] = df[item].astype('category').cat.codes
  33.     df = df.fillna(df.median())
  34.     df = pd.DataFrame(StandardScaler().fit_transform(df),columns=df.columns)
  35.     print(df.shape)
  36.     return df
  38. def order_by_kmeans(self):
  39.     '''
  40.     根据Kmeans聚类结果对变量进行排序
  41.     '''
  43.     kk = KMeans(n_clusters = self.n_clusters)
  44.     res = kk.fit_predict(self.df.T)
  46.     self.df = self.df.append(pd.Series(res,index=self.df.columns),ignore_index=True)
  47.     self.df.sort_values(by = self.df.shape[0]-1,axis=1,inplace=True)
  48.     self.df.drop(self.df.shape[0]-1,inplace=True)
  50.     print(self.df.shape)
  52. def corr_heat_map(self):
  53.     '''
  54.     计算相关矩阵，并使用pyecharts的heat_map呈现
  55.     '''
  57.     self.order_by_kmeans()
  59.     self.corr = self.df.corr(method="pearson")
  60.     self.corr = self.corr.round(3)
  61.     self.corr = self.corr.apply(lambda x: abs(x))
  62.     myvalues = []
  63.     for i in range(len(self.corr.index)):
  64.         for j in range(len(self.corr.index)):
  65.             tmp = [i, j, self.corr.iloc[i, j]]
  66.             myvalues.append(copy(tmp))
  67.     self.__setattr__('pairs',myvalues)        
  69.     heat_map = HeatMap(init_opts=opts.InitOpts(width="1440px", height="1440px"))\
  70.         .add_xaxis(list(self.corr.columns))\
  71.         .add_yaxis("corr", list(self.corr.index), myvalues) \
  72.         .set_global_opts(
  73.             title_opts=opts.TitleOpts(title="模型变量相关性"),
  74.             datazoom_opts=[opts.DataZoomOpts(is_show=True, is_realtime=True), ],
  75.             visualmap_opts=opts.VisualMapOpts(min_=-1.2, max_=1.2, pos_right=20),
  76.             toolbox_opts=opts.ToolboxOpts(is_show=True),
  77.             xaxis_opts=opts.AxisOpts(type_="category", is_scale=True, is_inverse=True, axislabel_opts=opts.LabelOpts(is_show=True, rotate=-60)),
  78.             yaxis_opts=opts.AxisOpts(is_scale=True, is_inverse=False, axislabel_opts=opts.LabelOpts(is_show=True, position="right")),
  79.             tooltip_opts=opts.TooltipOpts(is_show=True))\
  80.         .set_series_opts(label_opts=opts.LabelOpts(is_show=True, position="insideBottom"))
  82.     heat_map.render()
  85. def drop_hight_corr(self):
  86.     '''
  87.     根据上述算法，删除相关性高的变量
  88.     '''
  90.     cor_pair = self.pairs
  91.     cor_pair.sort(key=lambda x:x[2],reverse=True)
  92.     del_pair = []
  93.     del_col = []
  94.     for item in cor_pair:
  95.         if (item[0]==item[1])|(set(item[:2]) in del_pair)|(item[0] in del_col)|(item[1] in del_col):
  96.             continue
  98.         if item[2]>self.threshold:
  99.             c1 = self.corr.iloc[item[0],[x for x in range(self.corr.shape[0]) if x not in del_col]].mean()
  100.             c2 = self.corr.iloc[item[1],[x for x in range(self.corr.shape[0]) if x not in del_col]].mean()
  102.             del_col.append(item[0] if c1>c2 else item[1])
  103.             del_pair.append(set(item[:2]))
  104.         else:
  105.             break
  107.     del_col_name = self.corr.iloc[:,del_col].columns
  109.     return list(del_col_name)

if name == ‘main‘: c = cal_c(df, n_clusters=5, threshold=0.7)

  1. #在当前路径下产生的render.html文件即为相关矩阵热力图
  2. c.corr_heat_map()
  3. del_col = c.drop_hight_corr()

```

————————————————
版权声明：本文为CSDN博主「白白的一团团」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/baidu_39413110/article/details/106362118