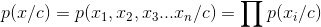解释一下朴素贝叶斯中考虑到的条件独立假设

讲一讲你眼中的贝叶斯公式和朴素贝叶斯分类差别

贝叶斯公式是完整的数学公式P(A/B) = P(A)P(B/A)/P(B)
朴素贝叶斯 = 贝叶斯公式 + 条件独立假设，在实际使用过程中，朴素贝叶斯完全只需要关注P(A,B)=P(A)P(B/A)即可

多项式：多项式模型适用于离散特征情况，在文本领域应用广泛，其基本思想是：我们将重复的词语视为其出现多次
- 因为统计次数，所以会出现0次可能，所以实际中进行了平滑操作
  - 先验平滑：
  - 后验平滑：
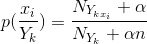
  - 两者形式非常像，区别就在先验平滑分母考虑的是平滑类别y个数，后验平滑分母考虑的是平滑特征对应特征x可选的个数
高斯：高斯模型适合连续特征情况，高斯公式
- 高斯模型假设在对应类别下的每一维特征都服从高斯分布（正态分布）
伯努利：伯努利模型适用于离散特征情况，它将重复的词语都视为只出现一次

出现估计概率值为 0 怎么处理
拉普拉斯平滑

朴素贝叶斯的优缺点？
优点：对小规模数据表现很好，适合多分类任务，适合增量式训练
缺点：对输入数据的表达形式很敏感（离散、连续，值极大极小之类的）

朴素贝叶斯与 LR 区别？
生成模型和判别模型
条件独立要求
小数据集和大数据集