风控算法或风控策略，确实需要很深、很广泛的技术储备，但是也需要很高的应用艺术和想象力。风控不像其他业务技术或算法，算法的出现本身就有了比较确定性的场景了，比如推荐，直接套用就行，但是很多算法在风控领域应用的时候，场景需要自己去挖掘和发现。
怎么抽象场景，怎么使用算法，就是一个艺术活了。下面用一个图异常检测算法的一个点举例说明。算法链接：OddBall-图异常点检测(见文末)
这篇文章，我相信很多读者看到是图算法，基本就放弃，认为需要要自己写很复杂的算法才能部署和实现，其实对这个算法充分理解后，简单的统计就能用了，难点在于对算法的理解，以及对业务中场景的抽象，我们看看这个算法的一个点。
算法如下：DominantPair（主导边）这个类型的风险，Dominant heavy links指“主导的边”，Ego-Net中存在某条边权重异常大，如下图所示。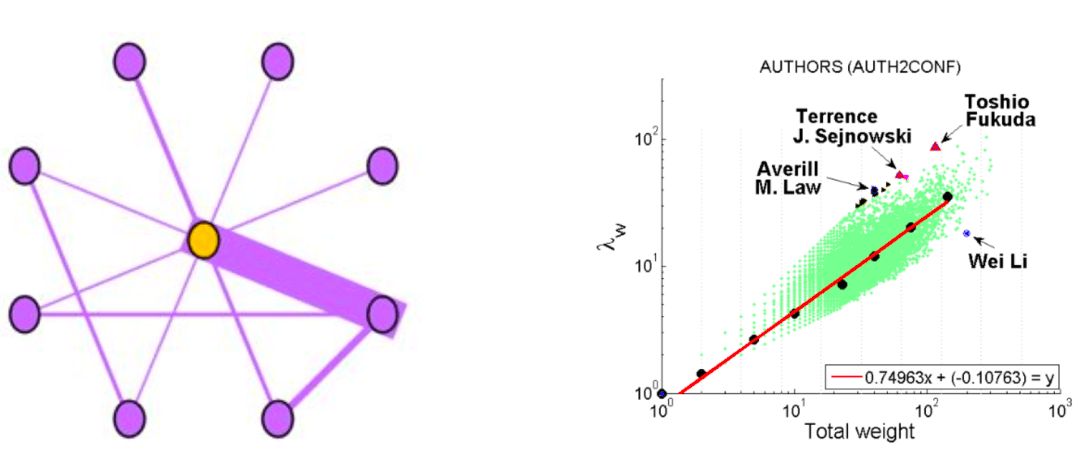
度量方法：主特征值～总权重，大多数节点Ego-net对应带权邻接矩阵中主特征值(principal eigenvalue，即最大特征值)～总边权重也服从幂律分布，其中系数 λ 表示Ego-net中边权均匀分布， λ 接近1表示存在DominantPair的情况，衡量的公式如下：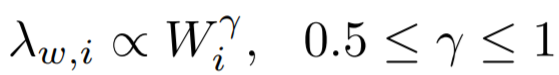
我们来简化下这个算法思想：其实一句话，就是一个点有很多个邻居，某个邻居权重占所有邻居总权重的比例特别大
再来个更具体的例子：一个商家一个月卖了10000个订单，100个消费者，其中一个消费者买了9900单，那这个消费者占比9000/10000=90%，形成了主导边，那这个商家可能就存在异常。我们其实只要统计商家的总订单，以及每个商家-消费者维度的订单聚合，然后相除就解决了，这就是个简单的SQL计算问题，完全不用什么复杂的写算法。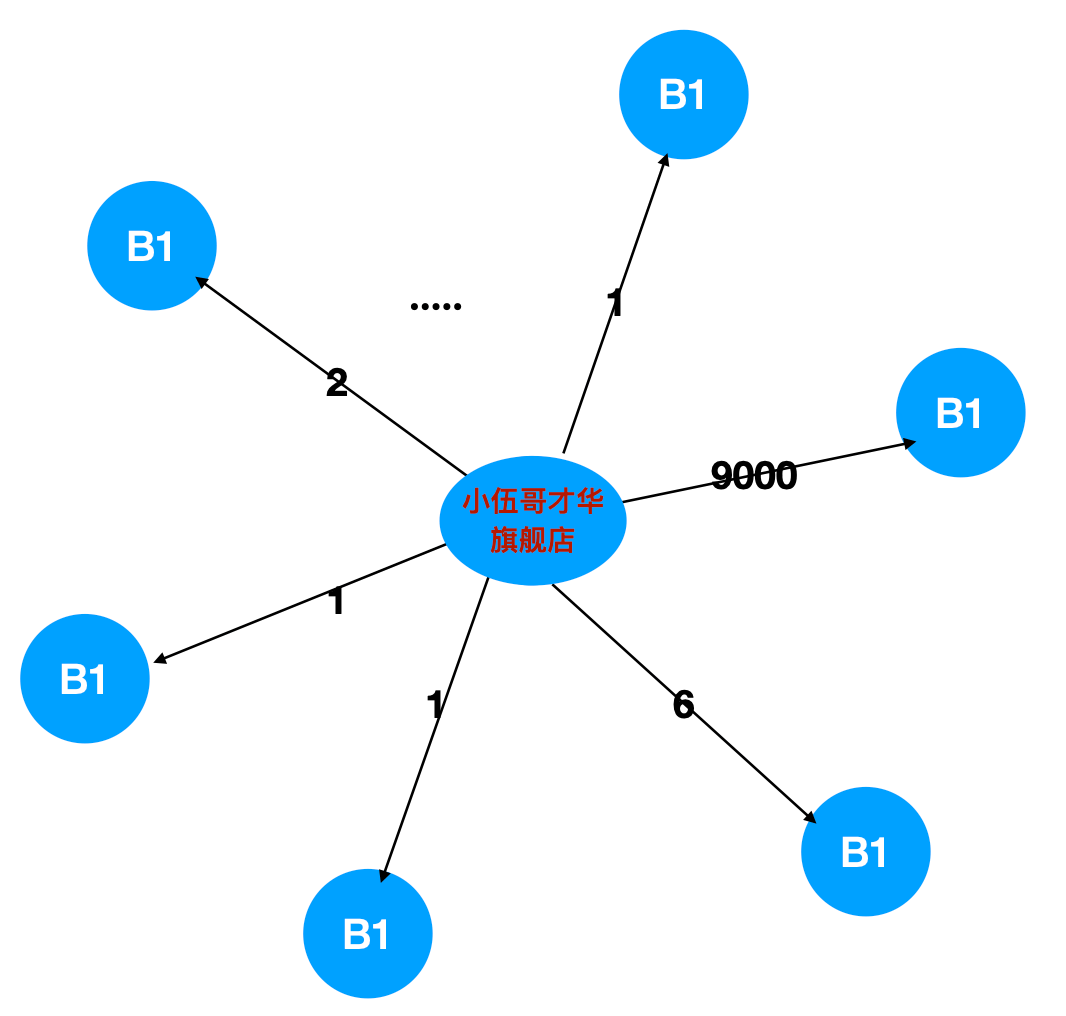
当然，这里的订单数可以换成金额
订单换成点击：可以监控恶意流量什么的
订单换成领券：可以监控羊毛党什么的
·········
商家和消费者也可以换成其他的角色，根据自己的平台设计这种监控指标，我觉得能发现传统发现不了的异常，因为很少有人这么思考过。
那消费者-换地址关系呢？情况就变了，权重大反而是正常的，小反而不正常，可能是黄牛什么的，因为正常人得地址，相对比较集中，就那个几个固定的。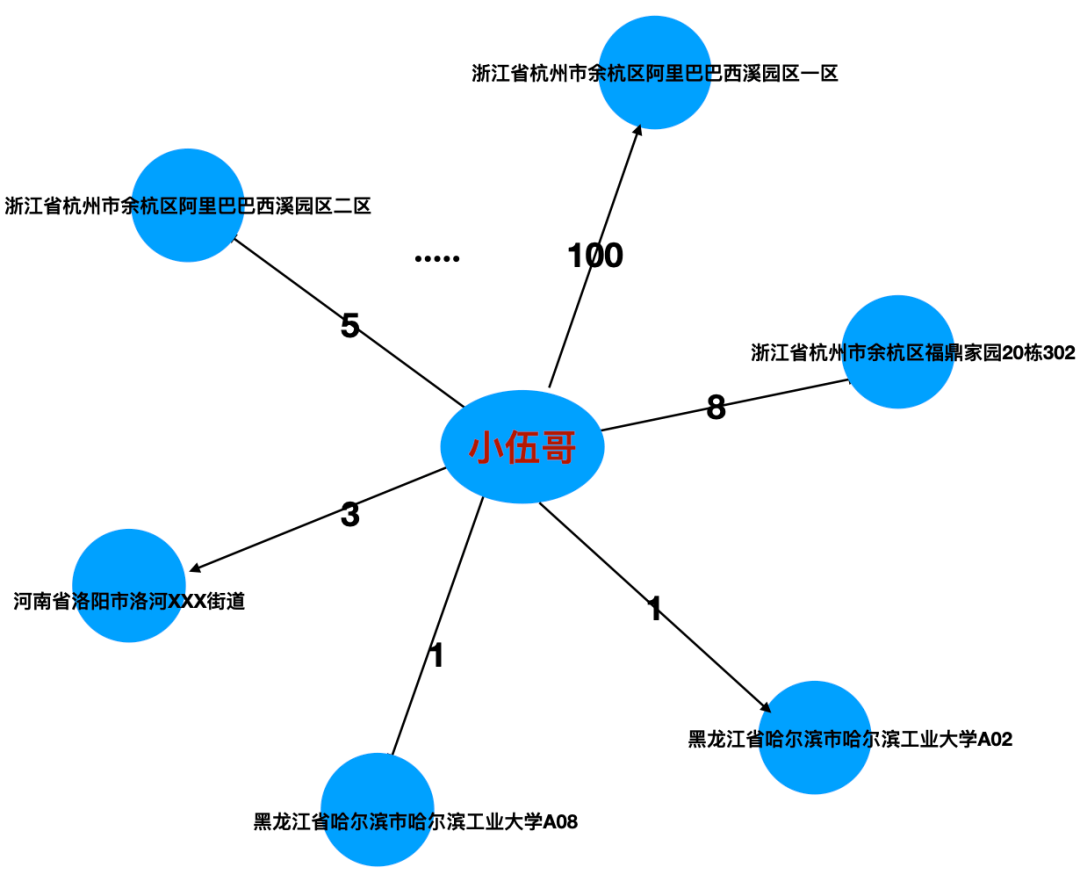
那消费者-充值手机呢？也是同样的，权重大反而是正常的，小反而不正常，可能是销赃款或者洗钱什么的。因为正常人，给自己手机充值，或者加几个家里人和同学什么的，有些账户给几千几万人充值，那可能就异常了。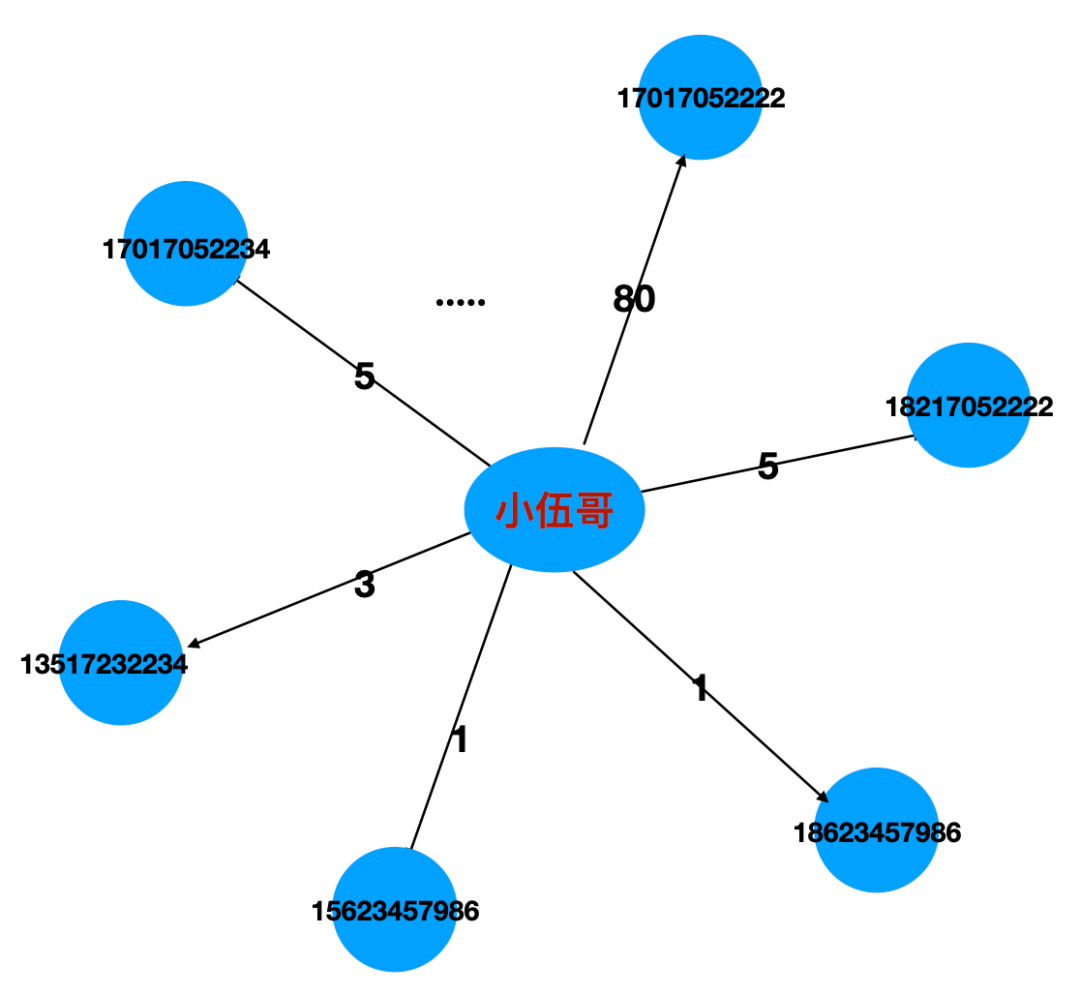
那这个是不是可以再抽象一点，比如消费者-购物类目关系网络，按道理，每个人的购物，基本均匀分布在不同的类目，有吃穿的也有用的，如果发现一个用户，大量购买集中在某些偏门的类目，那是不是有可能这个用户或者被购买的商家有异常？是不是要买制毒的原材料？是不是在图谋什么？或者在交易什么？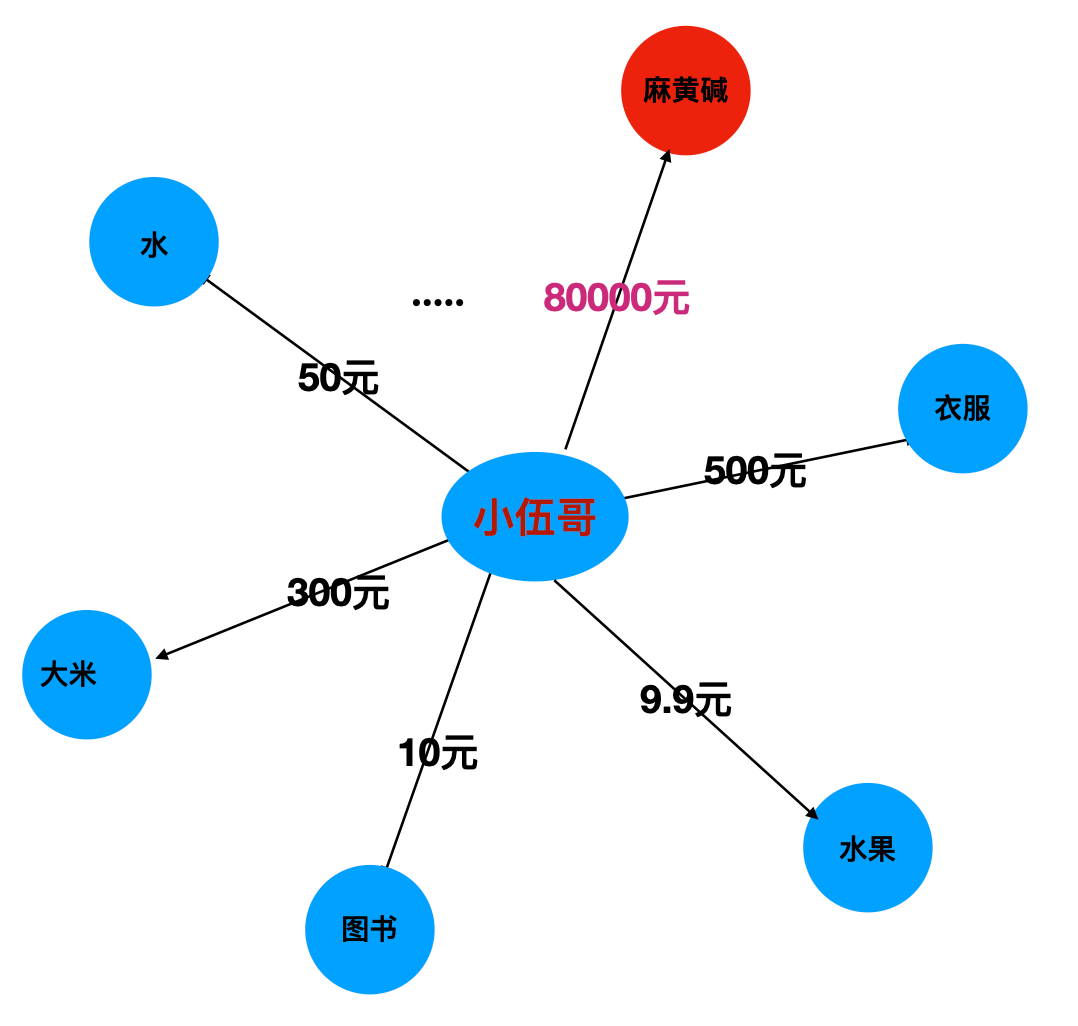
每个公司的业务不一样，但是很多思路，都是可以顺着这个算法的结构去思考的，需要充分理解算法，充分理解业务，充分的想象力。
我们看到了异常检测，看到了图，但是要更加深入的去看到业务与之匹配的地方，多维度的思考，联想，并进行应用，才能让算法产生价值，所以，风控，不仅是技术问题，也是艺术。
风控挖掘的乐趣，大抵也在此了。
一、概 述
基于图的异常检测分为 孤立点检测 和 异常群簇检测，本文是孤立点检测中较经典的论文，通过研究Ego-net总结几种异常模型及提供度量方式：
| 异常结构 | 含义 | 度量方式 |
|---|---|---|
| CliqueStar | 呈星状或者团状结构 | 边数~节点邻居数 |
| HeavyVicinity | 总边权重异常大 | 总边权重~边数 |
| DominantPair | 存在某条权重异常大的边 | 主特征值~总边权重 |
文章调查了Ego-net中存在的异常模式，并给出了检测异常模式的依据基于上述模式，提出了OddBall，一种用于异常点检测的无监督方法，将OddBall应用于真实数据集，并验证了算法的有效性
论文名称：OddBall: Spotting Anomalies in Weighted Graphs
论文地址：http://www.cs.cmu.edu/~mmcgloho/pubs/pakdd10.pdf
代码地址：https://www.andrew.cmu.edu/user/lakoglu/pubs.html#code
二、Ego-net（中心节点）
以中心节点(ego)及其邻居组成的子图，一般用于研究个体性质以及局部社区发现，本文仅考虑一阶邻居，这是为了减少计算量并提和高可解释性。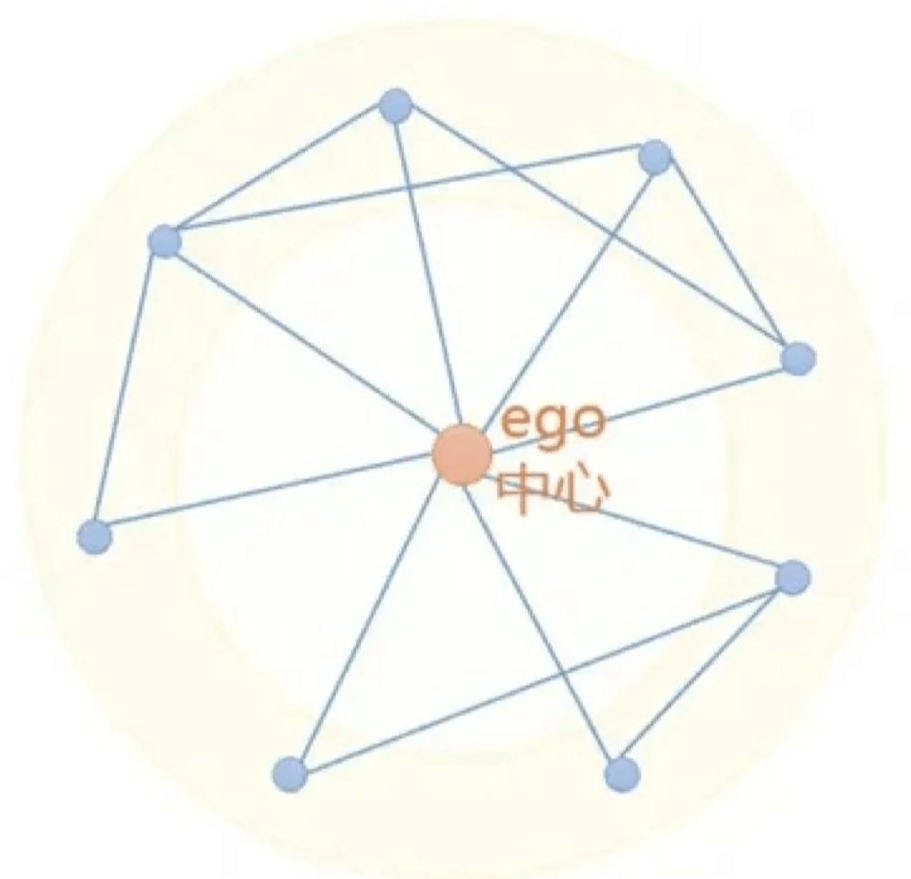
三、Ego-net模式及度量方法
1 、CliqueStar（基于密度）
基于密度的方法可以识别出下面两种Ego-net的异常结构：
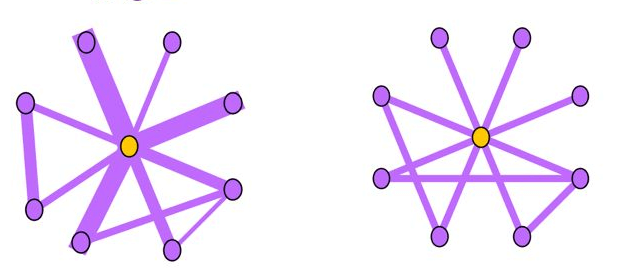
Near-Star：在正常的社交网络中，我们通常认为朋友之间可能会相互认识，因此一阶Ego-net中的邻居之间没有任何关联是非常可疑的，近似星型，邻居之间很少联系（如通话关系网络中的中介、电催人员、营销号码，他们大量的联系别人，然而联系人中之间几乎没啥联系），这种结构的Ego-net被称为star，如下图所示，中心节点与大量节点存在关联，但是邻居之间无联系或者联系很少。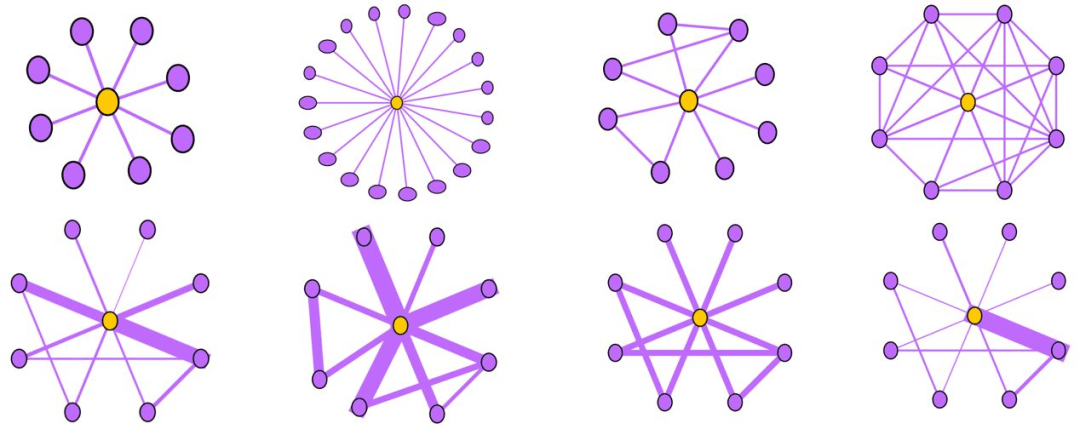
Near-Clique：与上述相反，邻居之间存在大量关联也是非常可疑的，这种结构的Ego-net被称为cliques。正如下图所示，中心节点与大量节点存在关联，邻居之间的联系非常密集，近似环状，邻居之间联系紧密（如某个讨论组、恐怖组织）。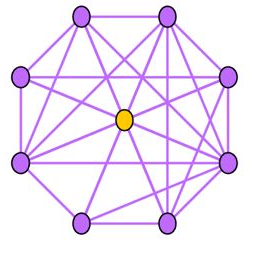
度量方法：边数～邻居数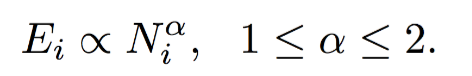
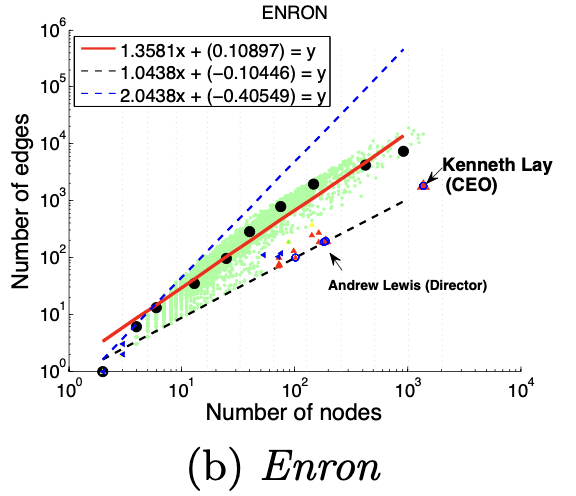
如下图所示，可以看出大多数节点Ego-net中边数 E 与邻居数 N 服从幂律分布（对数坐标后呈线性）、给定某节点i对应的 Ei 、Ni ，求出幂律系数 α ，若：
α 接近1（黑色虚线），节点i的Ego-net呈现Near-Clique
α 接近2（蓝色虚线），节点i的Ego-net呈现Near-Star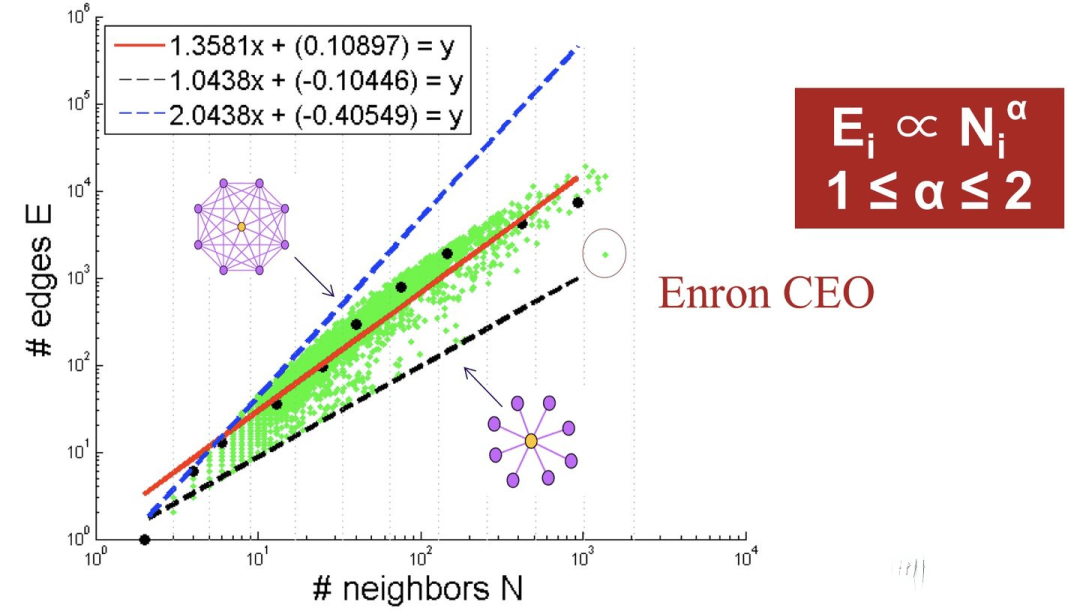
红线是拟合中位数，蓝色和黑色虚线是边界线。
大多数Graph都遵循该模式：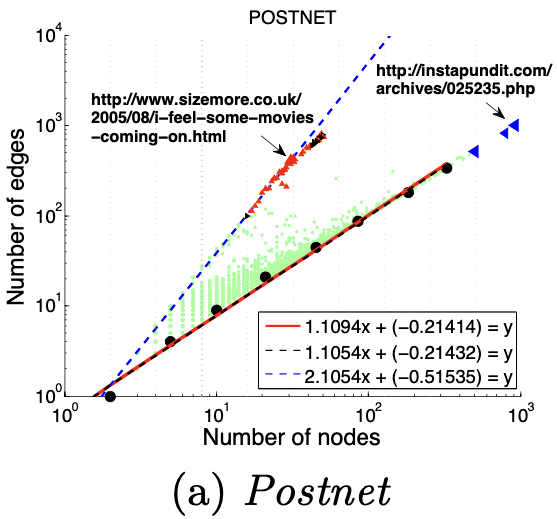
2、HeavyVicinity(权重)
HeavyVicinity指“较重的邻居“，Ego-net中边数一定时，总边权重异常大（如骗贷者通过频繁拨打电话伪造通话记录），中心节点与一小部分节点之间存在权重非常大的关联也是可疑的，如骗贷者通过频繁拨打电话伪造通话记录。正如下图所示，中心节点与少部分节点之间的连接权重非常大。
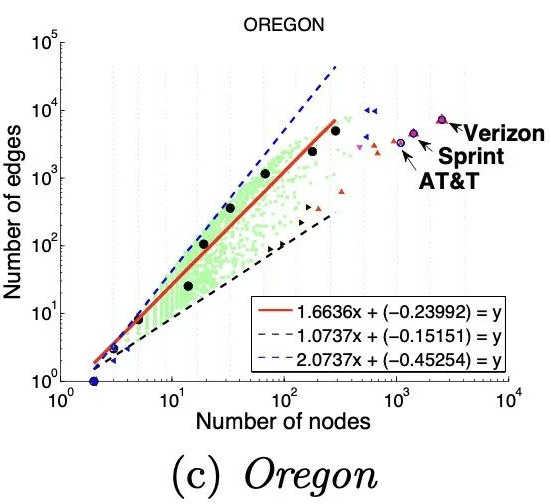
度量方法：总边权重～边数
大多数节点Ego-net中总边权重～边数也服从幂律分布（对数坐标）， β 越高表示越异常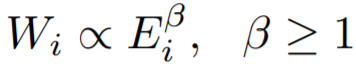
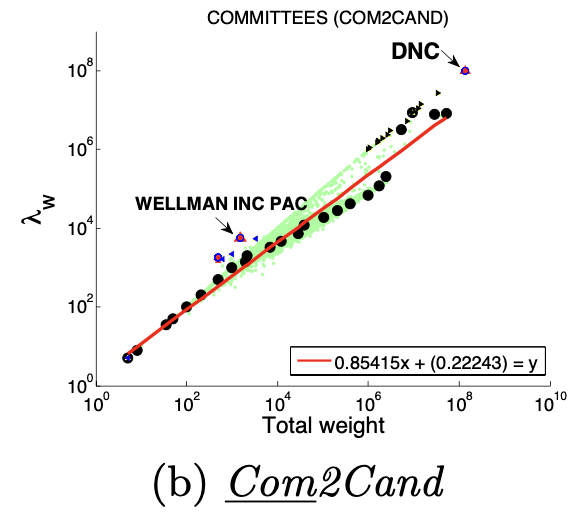
图（a）选举中，民主党（DNC）的大量的资金给为数不多的候选者
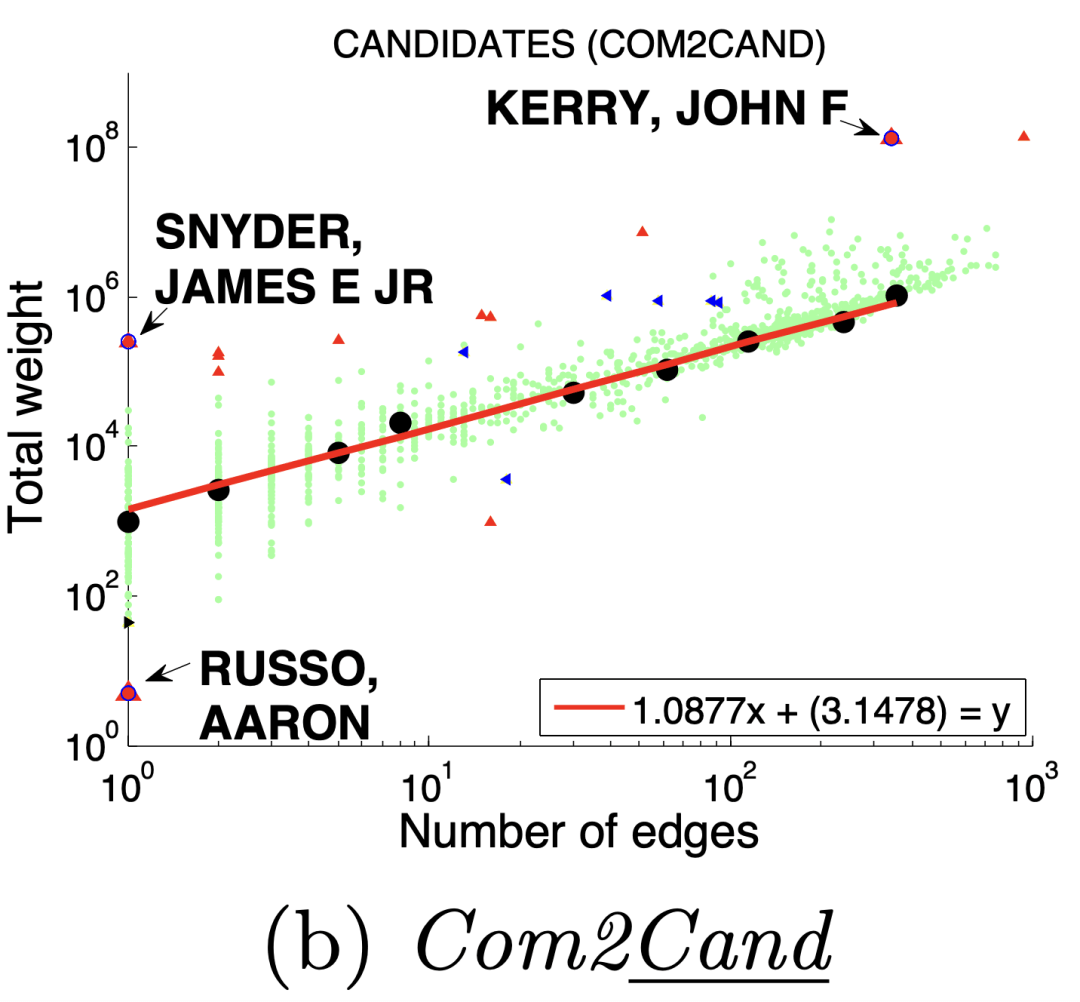
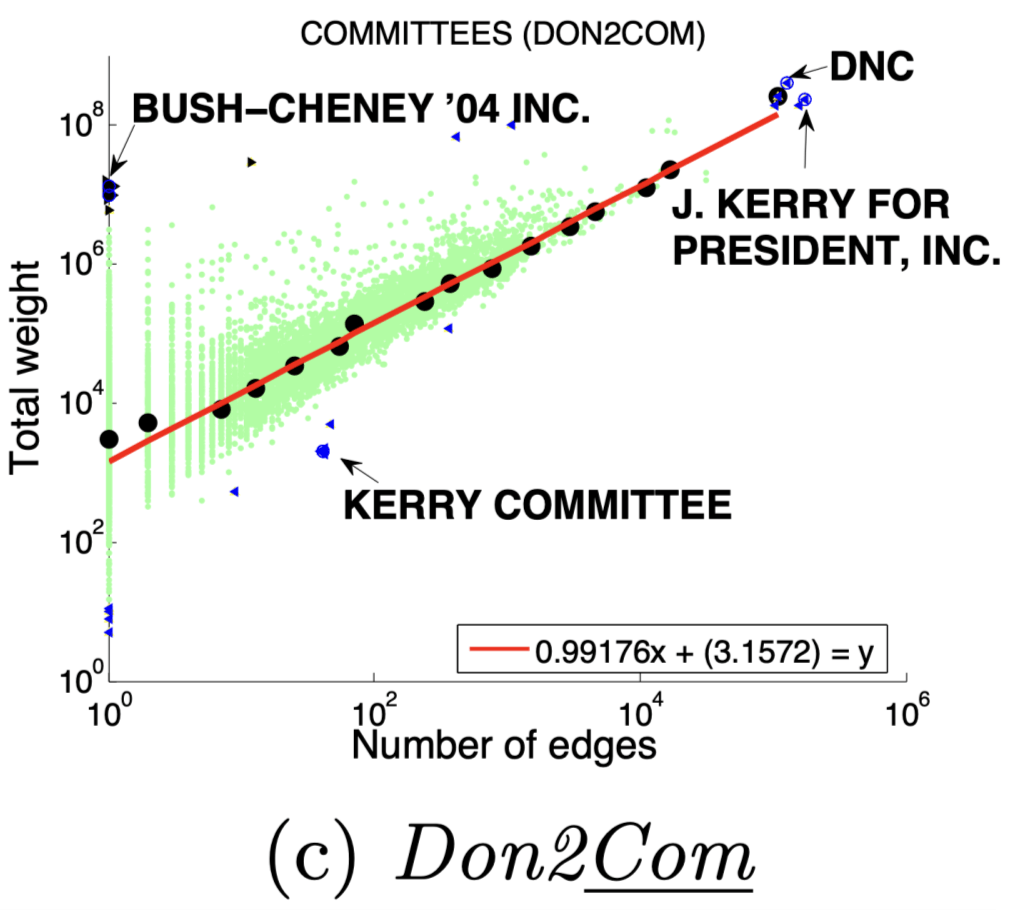
3 、DominantPair（主导边）
Dominant heavy links指“主导的边”，Ego-Net中存在某条边权重异常大（如学者投稿会议网络中，“Toshio Fukuda” 拥有115篇papers，投稿了17个会议，但其中87篇pager投稿了一个ICRA）：
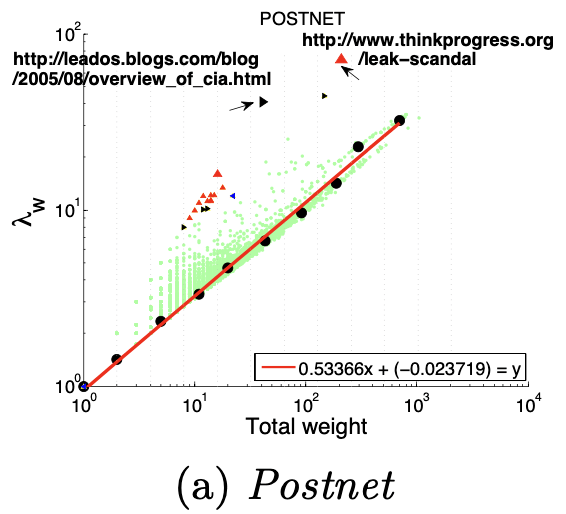
度量方法：主特征值～总权重
大多数节点Ego-net对应带权邻接矩阵中主特征值(principal eigenvalue，即最大特征值)～总边权重也服从幂律分布，其中系数 λ 表示Ego-net中边权均匀分布， λ 接近1表示存在DominantPair的情况。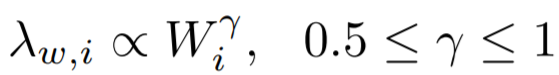
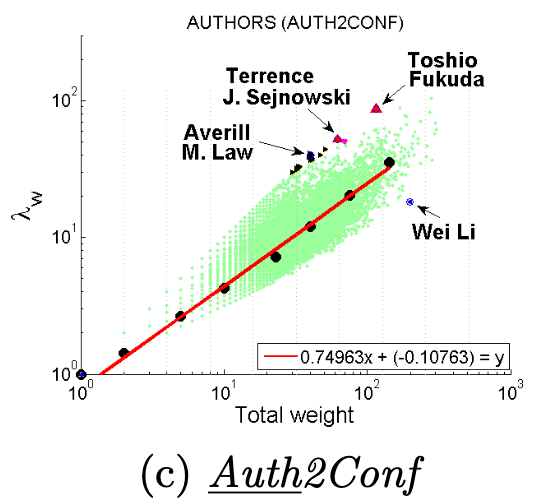
四、OddBall异常检测算法
OddBall由out-line(i)和out-lof(i)两部分组成：
out-line：计算实际点与拟合直线（红线）的偏离程度。
out-lof：但out-line但会存在“缺陷是无法识别离正常点很远，但与拟合直线很近的异常点”的缺陷,故结合传统基于密度的方法LOF（也可以选其他的）。
二者集成方式先求出两个score，然后归一化（除以最大值）后求和：
out-score(i)=out-line(i)+out-lof(i)
1、out-line
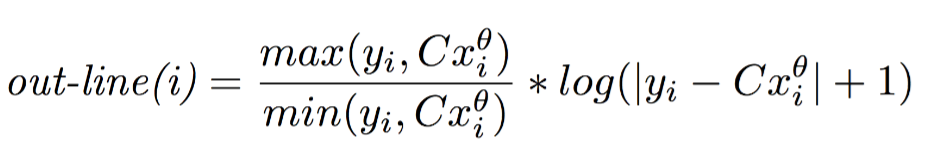
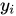为实际值，
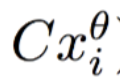为在拟合直线（正常点）上的预测值，二者相减为偏离程度／异常程度取- log是为了平滑
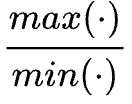为惩罚系数：实际值偏离正常的倍数
2、out-lof
outline的缺陷：无法识别红框内的节点，故引入LOF，详情可参考：https://zhuanlan.zhihu.com/p/28178476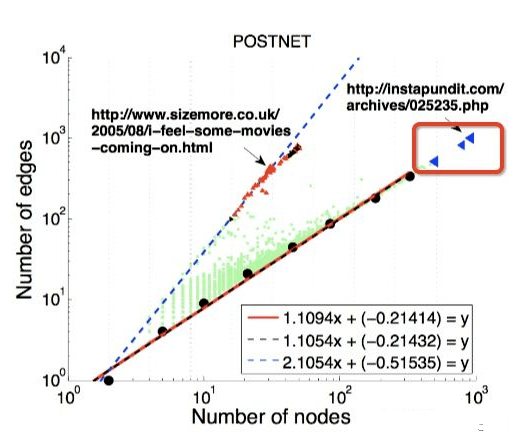
五、相关思考
本文中仅考虑了节点的一阶子图，将子图范围扩展到二阶或者是更大的局部子图是否会效果更好？检测模式依赖的特征是否具有鲁棒性？
若有收获，就点个赞吧
0 人点赞
