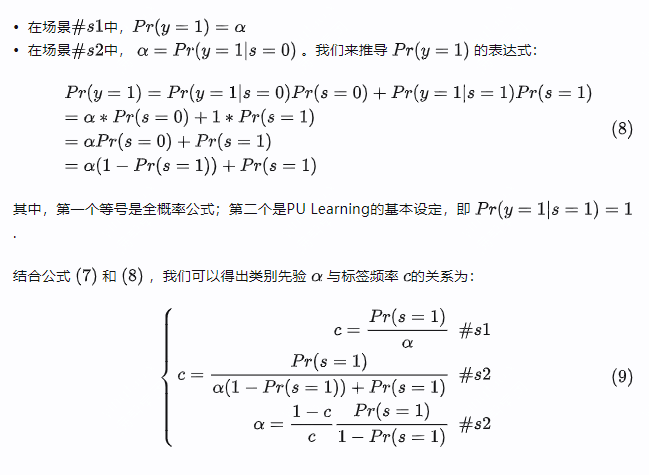- 58同城风控智能化实践
- PU-Learning 原理介绍
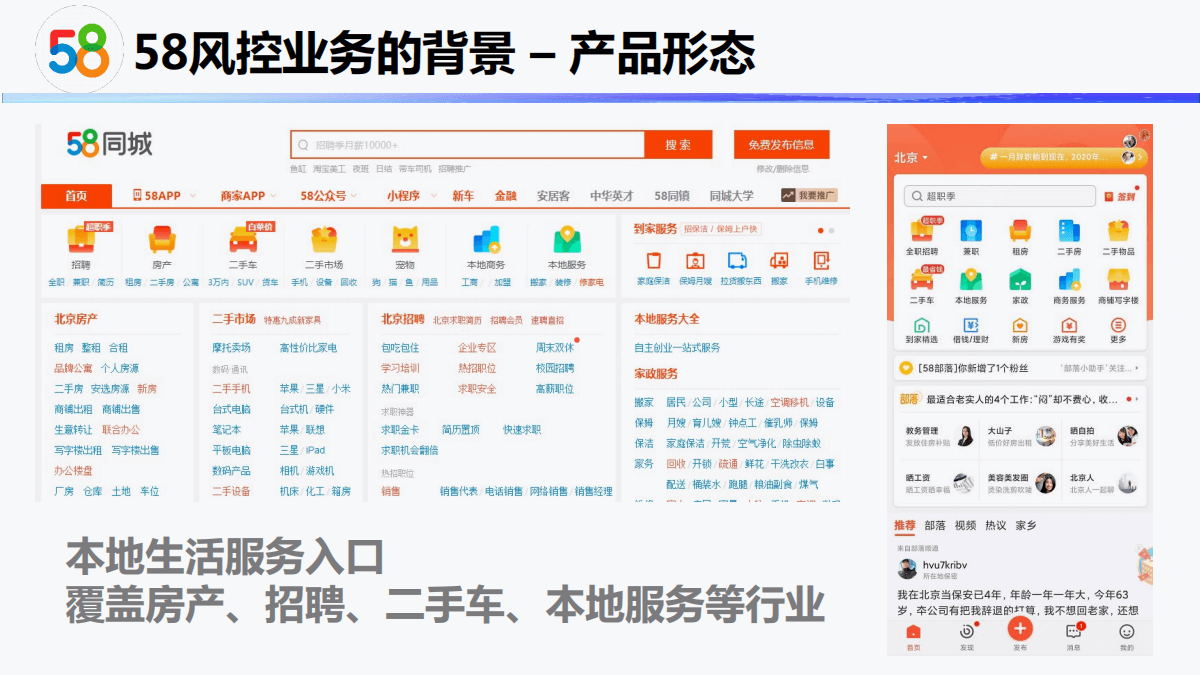
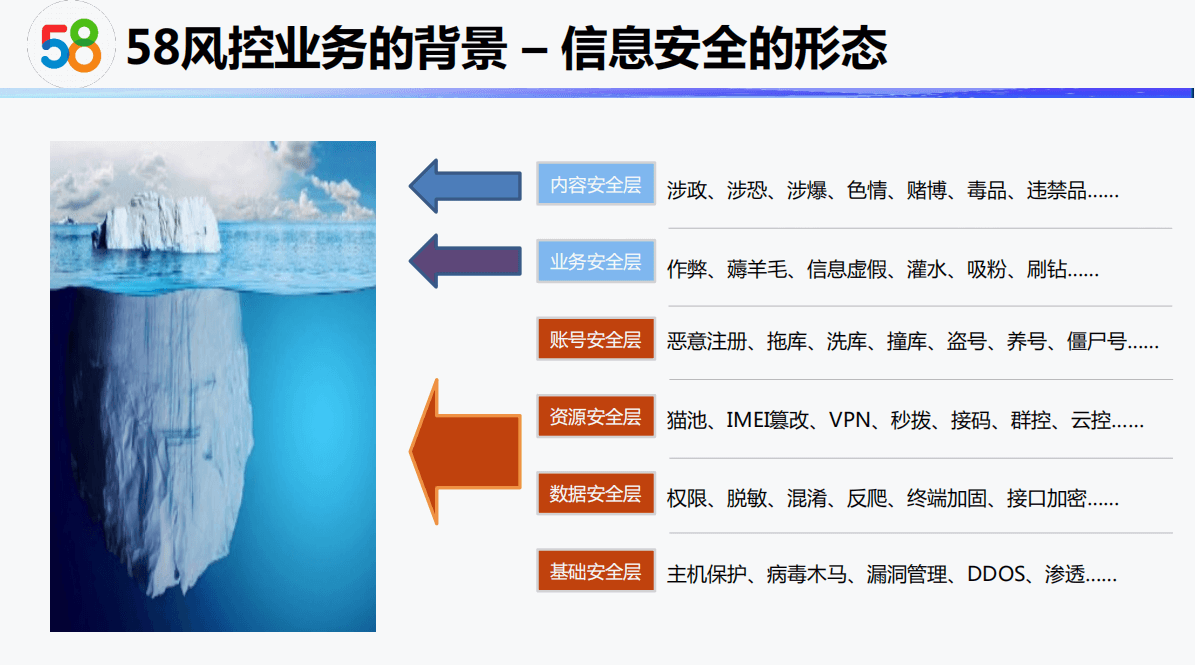
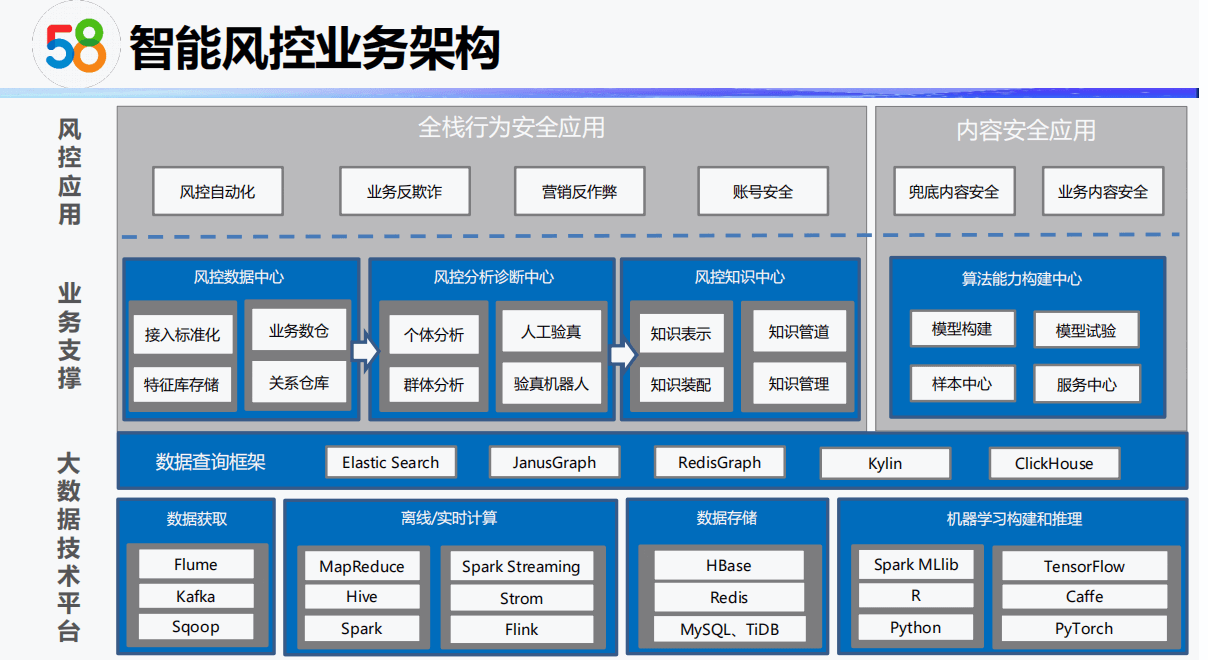
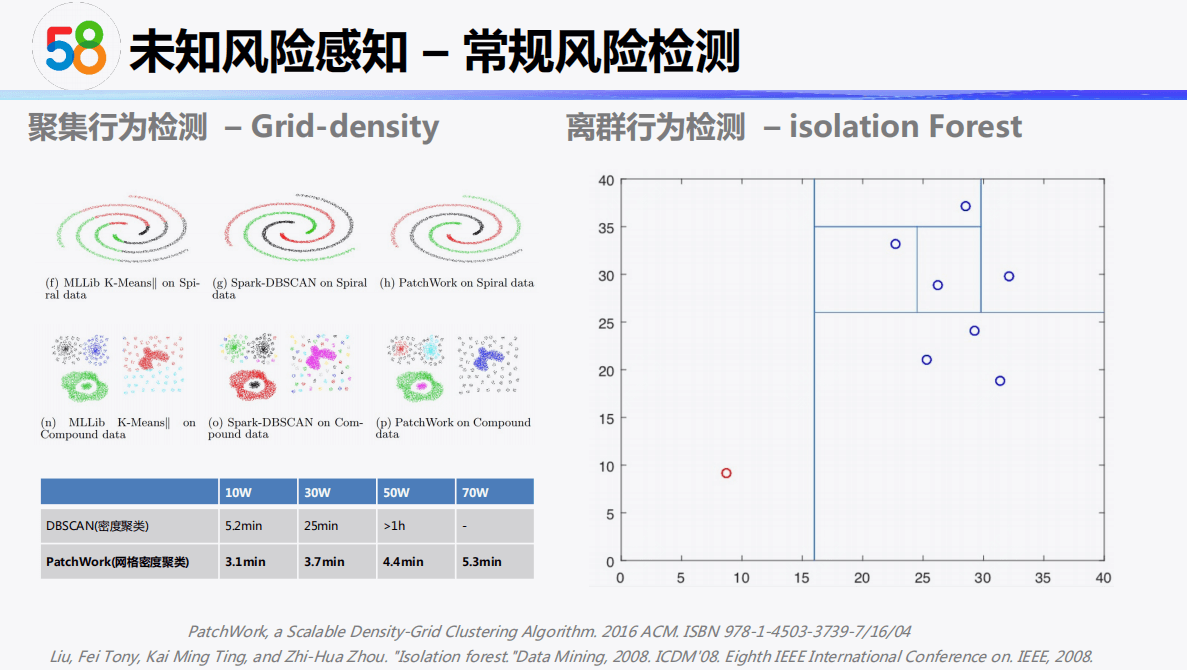
- 风控业务背景
- Part 1. PU Learning的基本概念
- Part 2. PU Learning的基本假设
- 2.1 打标机制(Label Mechanism)
- 2.2 数据假设(Data Assumptions)
- Part 3. PU Learning的评估指标
- Part 4. 两阶段技术(Two-step PU Learning)
- Part 5. 有偏学习(Biased PU Learning)
- Part 6. 融入类别先验(Incorporation of the Class Prior)
- Part 7. 类别先验的估计方法
- Part 8. Active Learning与PU Learning的对比
- Part 9. 总结
- 致谢
- 版权声明
- 2-3 DataFunSummit-智能风控技术峰会分享-龚灿-20210515
- 1-2 DataFunSummit-智能风控技术峰会-JDT
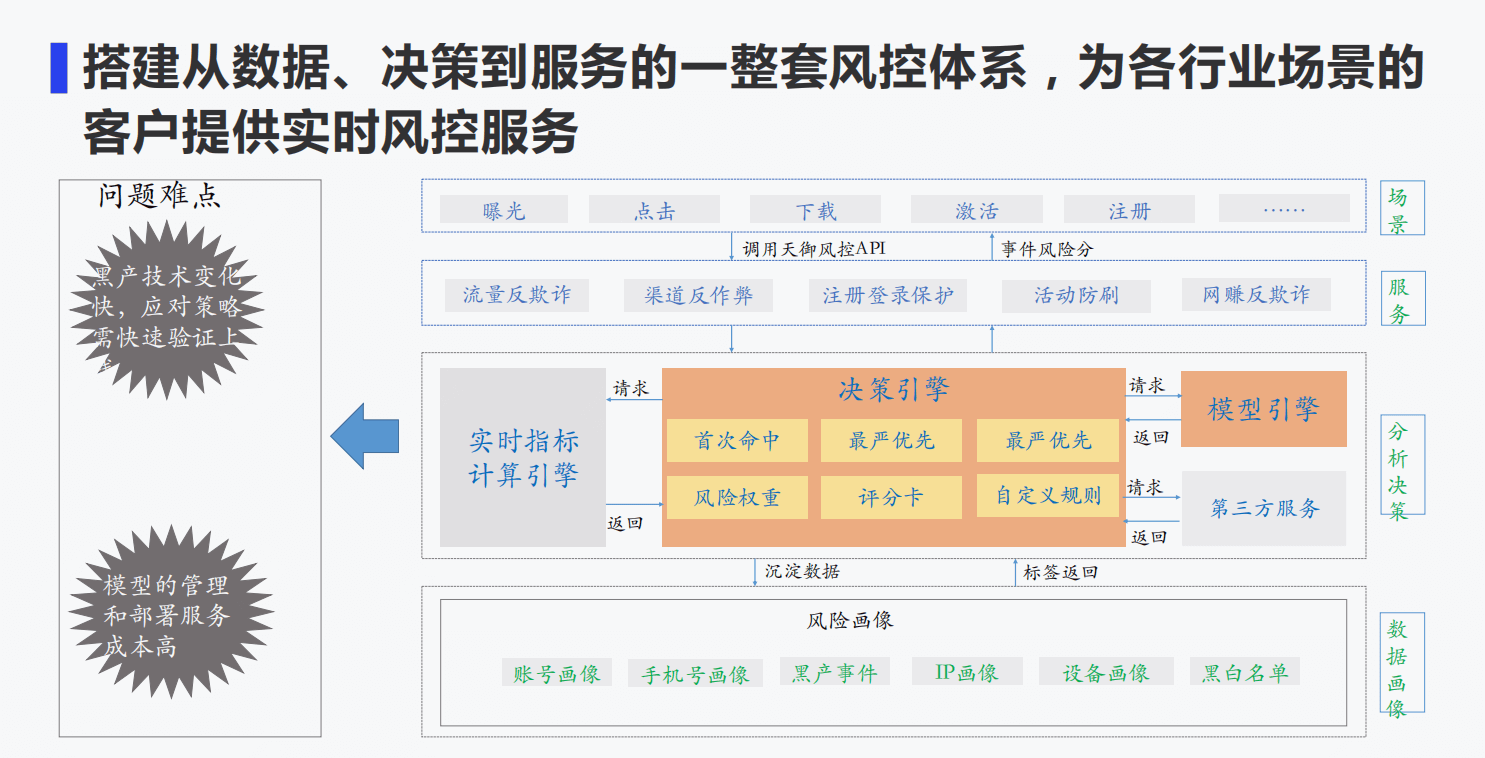
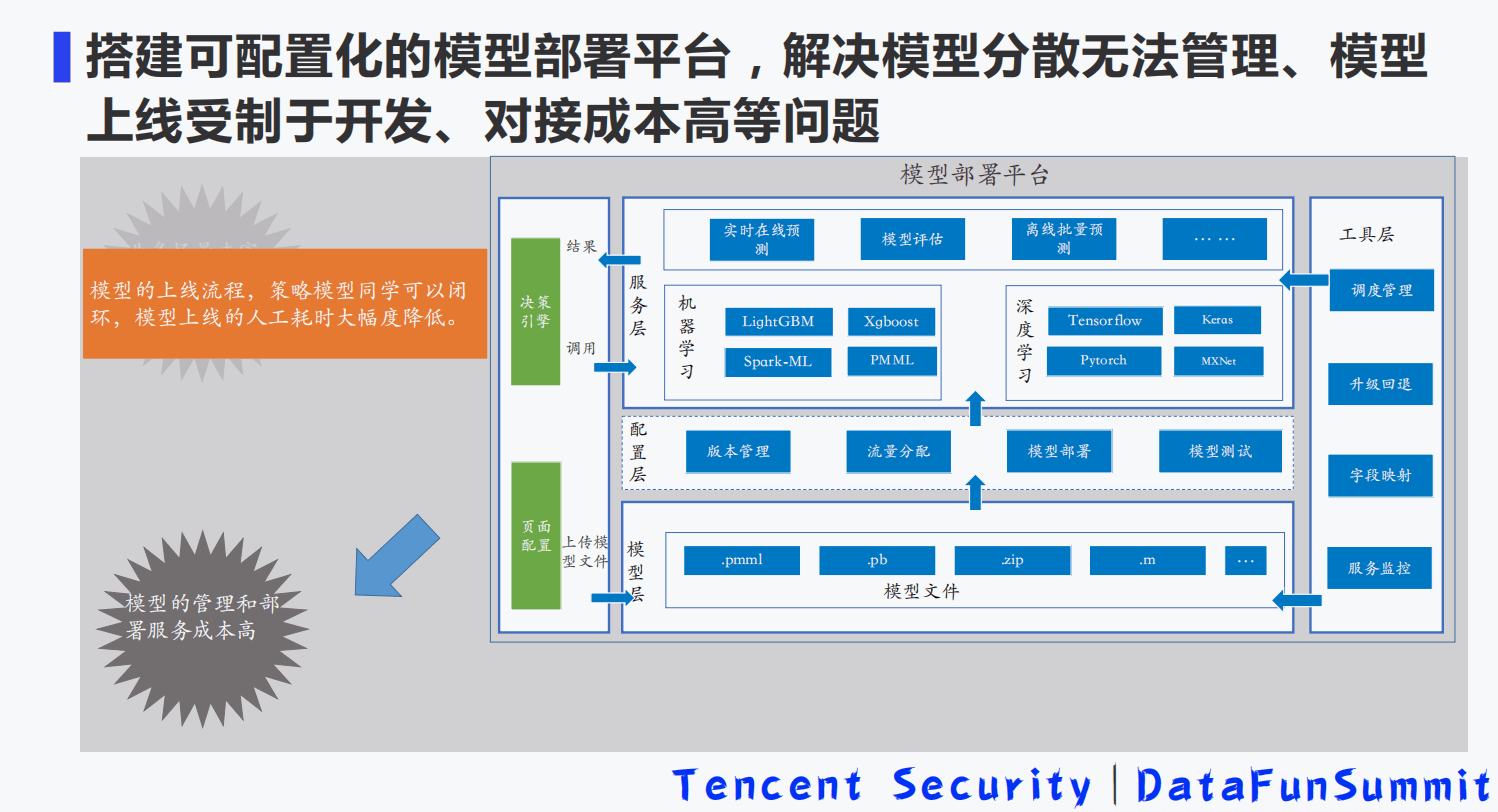
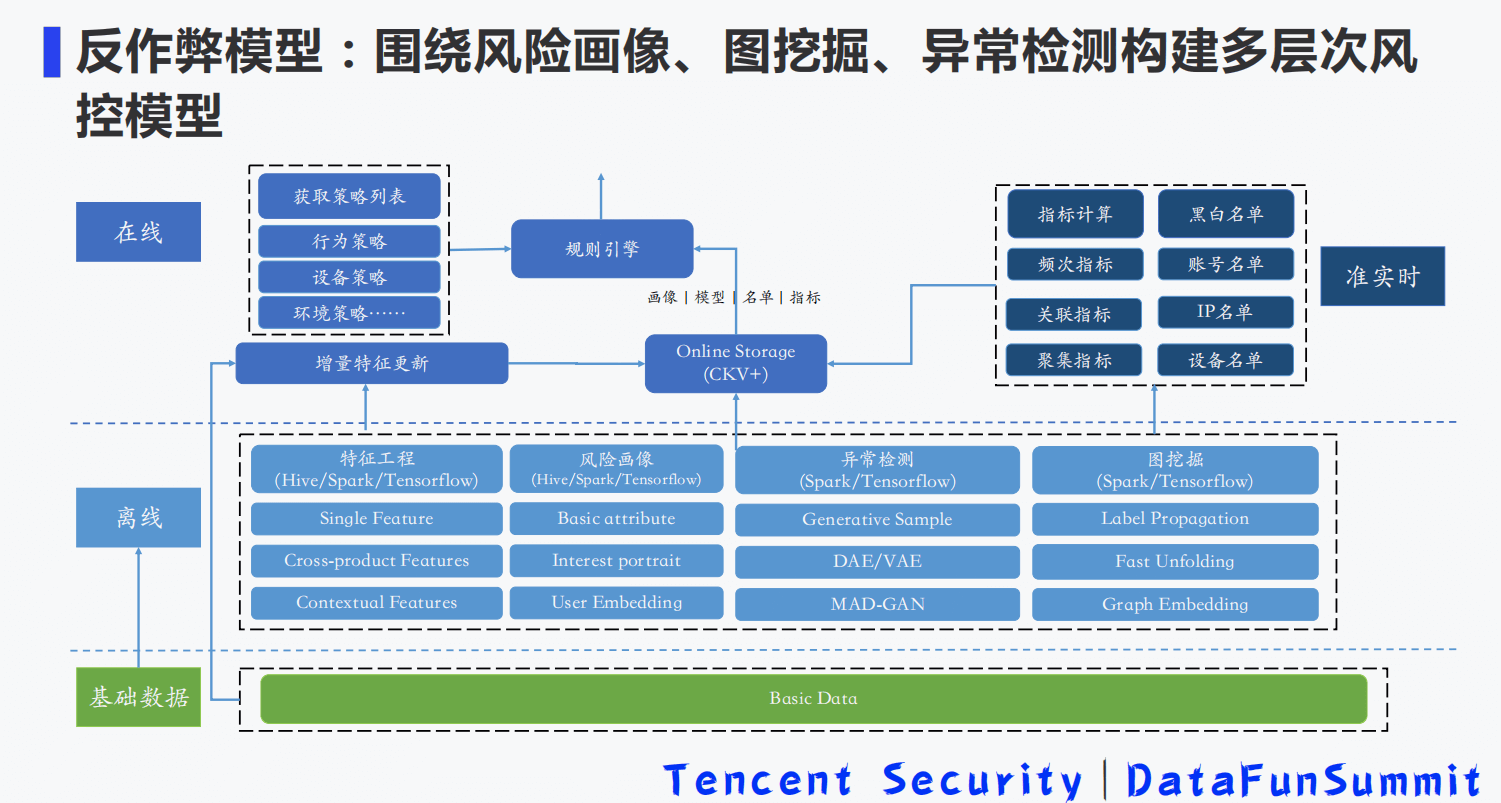
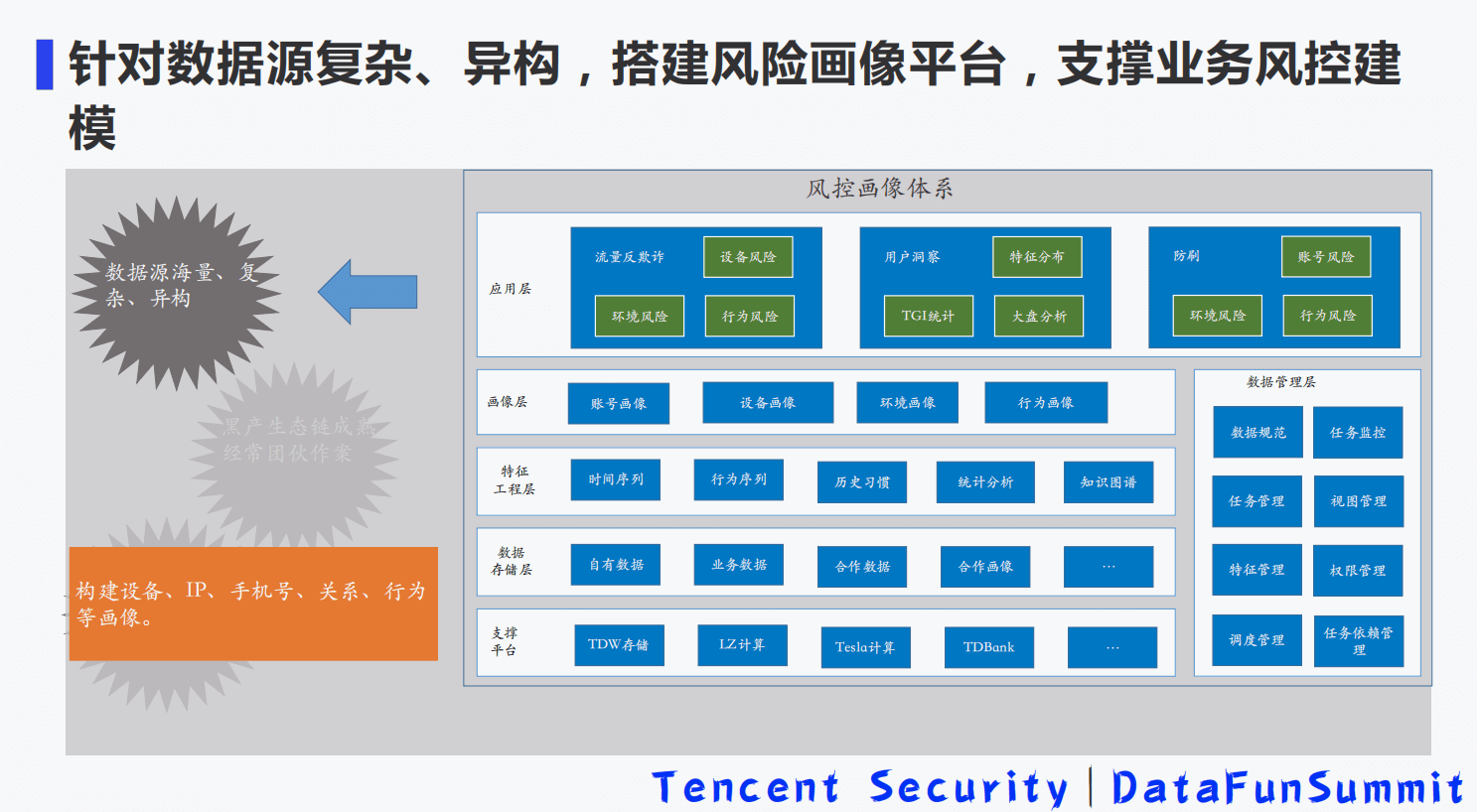
- 9-2 基于全栈式实时风控引擎的流量反作弊平台建设.pdf
58同城风控智能化实践
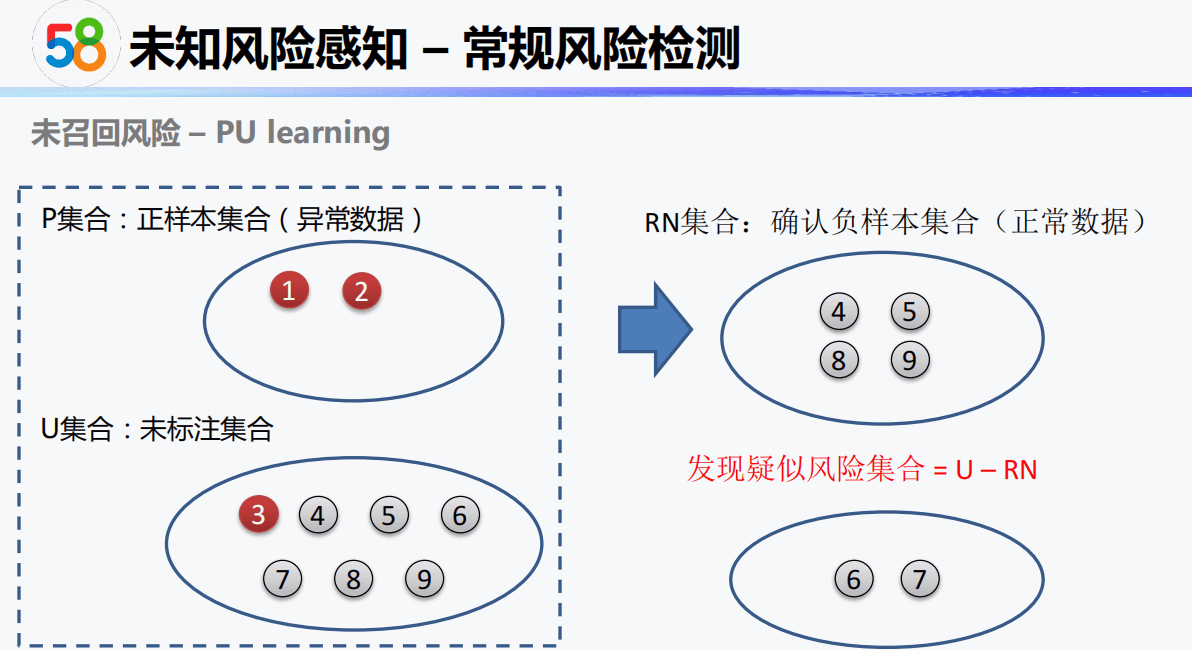
PU-Learning 原理介绍
来源:https://zhuanlan.zhihu.com/p/98887617
风控业务背景
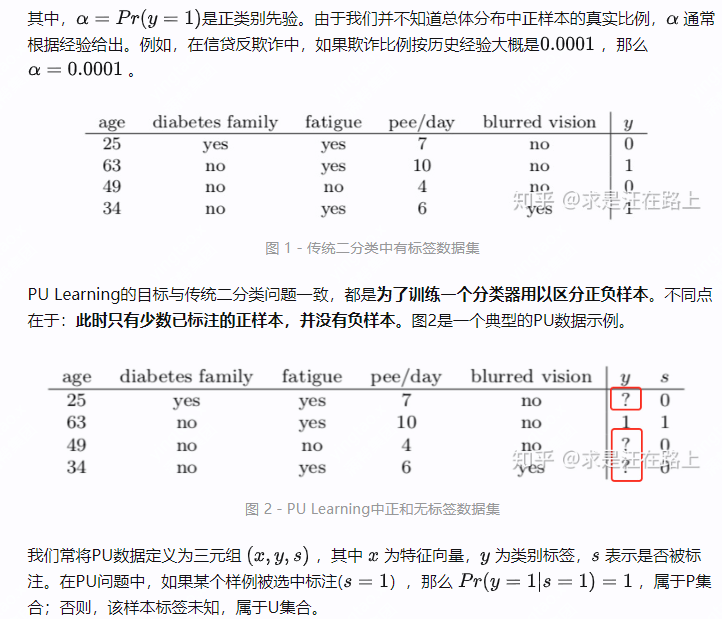
在实际分类场景中,我们经常会遇到类似这样的问题:只有已标记的正样本,以及未标记的样本。比如金融风控场景,只有部分用户被标记为欺诈用户,剩下的大量用户未被标记。虽然这其中大多数信用良好,但仍有少量可能为欺诈用户。
为了方便操作,我们可以将未标记的样本都作为负样本进行训练,但存在几个缺陷:
- 正负样本极度不平衡,负样本数量远远超过正样本,效果很差。
- 某些关键样本会干扰分类器的最优分隔面的选择,尤其是SVM。
如何辨别未标记样本中的正负样本,提升模型准确度,就成为一个值得思考的问题。PU Learning就是解决这种场景的一种学习方法。
本文尝试回答以下几个问题:
- How can we formalize the problem of learning from PU data?
- What assumptions are typically made about PU data in order to facilitate
the design of learning algorithms? - Can we estimate the class prior from PU data and why is this useful?
- How can we learn a model from PU data?
- How can we evaluate models in a PU setting?
- When and why does PU data arise in real-world applications?
- How does PU learning relate to other areas of machine learning?
目录
Part 1. PU Learning的基本概念
Part 2. PU Learning的基本假设
Part 3. PU Learning的评估指标
Part 4. 两阶段技术(Two-step PU Learning)
Part 5. 有偏学习(Biased Learning)
Part 6. 融入先验类别(Incorporation of the Class Prior)
Part 7. 先验类别的估计方法
Part 8. Active Learning与PU Learning的对比
Part 9. 总结
致谢
版权声明
参考资料
Part 1. PU Learning的基本概念
在传统二分类问题中,训练集中所有样本都有明确的0-1标签,即正样本(y=1)和负样本(y=0)。图1是一个二分类问题的数据集示例。同时,这些样本满足独立同分布,即: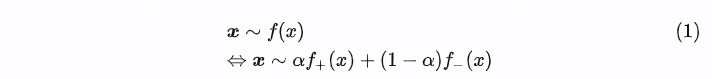
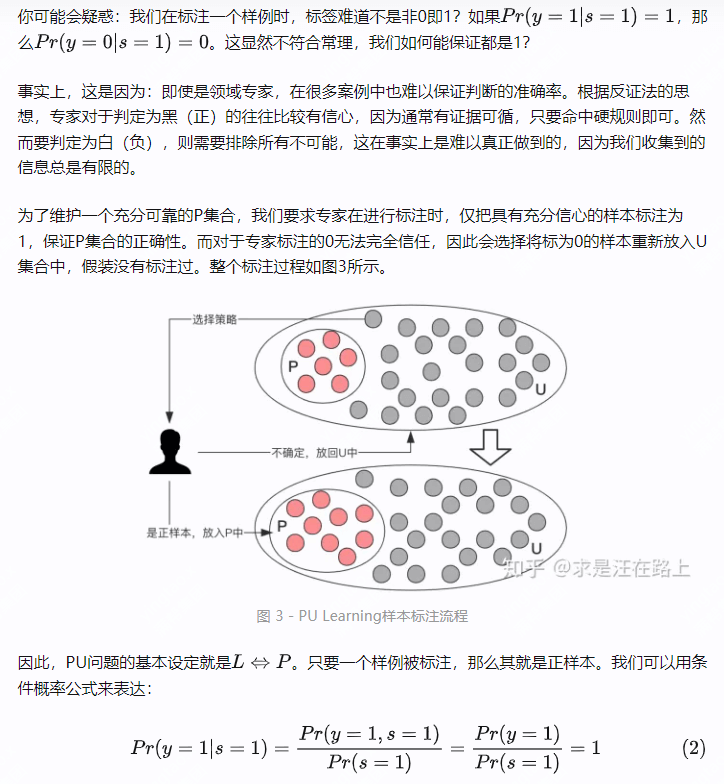
在了解样本标注流程后,我们又会遇到一个问题:如果从U集合中完全随机选择样例进行标注,发现不是正样本就放回,那岂不是效率很低?
因此,我们需要采取某种打标机制(Labeling Mechanism)从U中选择样本。同时,最理想的情况是每次都是从U集合中的隐式的“P”集合中选择,再经专家标注验证后,加入显式的P集合中。那么,我们就可以节省很多成本,P集合也能得到快速扩充!
在信贷风控中,我们会利用信用评分卡给客户打分,按信用分排序后,就可以进行拒绝或放贷。同样地,我们也需要定义一个倾向评分模型(Propensity Score),用以预测U集合中样本被选中的可能性(倾向)。

Part 2. PU Learning的基本假设
至此,你已经理解PU Learning的问题设定:一个是P集合,另一个是U集合。有标签和正标签是等价的。我们发现,只有两种可能性可以解释一个样例为什么没有标签:
- 是负样本。按PU Learning的定义,我们对于专家标注的0无法完全信任,因此会选择将标为0的样本重新放入U集合中,假装没有标注过。
- 是正样本。只是没有被打标机制所选中,所以无法观察到其表现。
因此,为了从PU数据中学习模型,我们从以下2个维度去设定一些假设:
打标机制(Label Mechanism)
类别分布(Class Distributions)
2.1 打标机制(Label Mechanism)
本节主要介绍构建选择模型时的一些假设。
1. 完全随机选择(Selected Completely At Random,SCAR):
2. 随机选择(Selected At Random,SAR):
3. 概率差距(Probabilistic Gap):
假设1:完全随机选择(Selected Completely At Random,SCAR)
Labeled examples are selected completely at random, independent from their attributes, from the positive distribution.
有标签样本完全是从正样本分布中随机选择的,且与本身的特征属性无关。
如图5所示,从x和y两个维度观察,x轴和y轴都是无偏均匀采样。
图 5 - 完全随机选择(SCAR)-PU数据
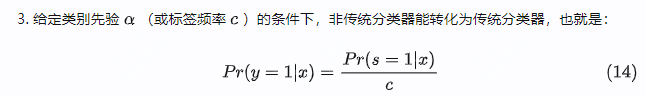
假设2:随机选择(Selected At Random,SAR)
The probability for selecting positive examples to be labeled depends on its attribute values.
有标签样本是从正样本分布中随机选择的,但与本身的特征属性有关。
如图6和图7所示,我们从x和y两个维度观察,虽然y轴上是均匀采样,但x轴上并不是,说明是有偏采样。造成这个现象的主要原因是——我们根据样本属性进行筛选。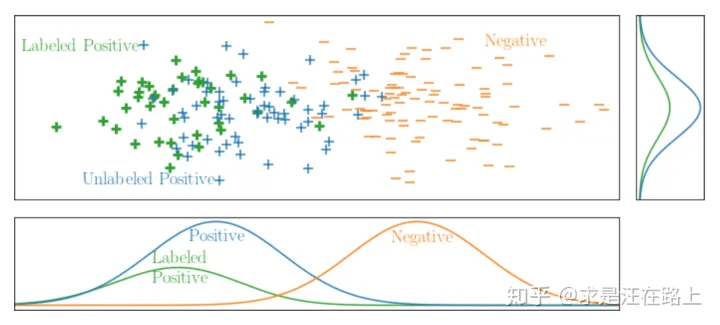
图 6 - 随机选择(SAR) 和概率差距(PG)-PU数据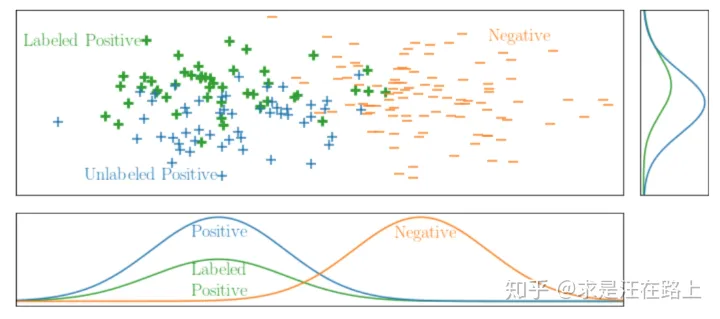
图 7 - 随机选择(SAR) -PU数据
2.2 数据假设(Data Assumptions)
本节主要对样本属性、标签等方面提出假设。
4. 负向性(Negativity):假设所有无标签样本都属于负类。
5. 分隔性(Separability):假设正负样本自然存在间隔。
6. 平滑性(Smoothness):假设相似的样本具有相同的标签。
假设4:负向性(Negativity)
The unlabeled examples all belong to the negative class.
假设U集合所有样本都属于负类。
尽管该假设不符合常理,但在实践中经常采用。主要原因在于:
- 我们已有P集合,只需要再有N集合,我们就可以直接归于成熟的二分类问题来解决。
- 作为EM算法中初始化的第一步,把U集合等同于N集合,然后不断迭代修正,最终收敛到一个稳态。
假设5:可分性(Separability)
The two classes of interest are naturally separated
始终存在一个分类器,能把正负两类然完全分开。

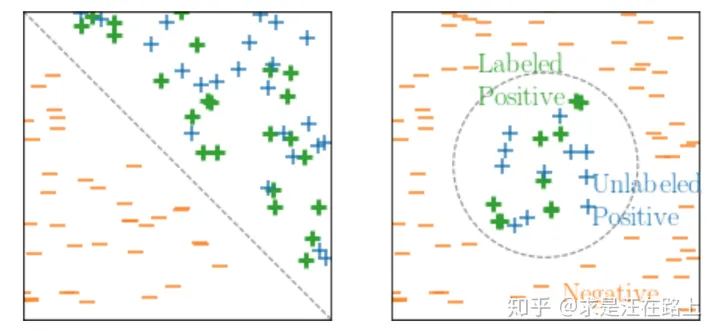
图 8 - 正负样本完美分隔
假设6:平滑性(Smoothness)
If two instances x1 and x2 are similar, then the probabilities Pr(y = 1|x1) and Pr(y = 1|x2) will also be similar.
如果两个样本相似,那么预测概率评分也是基本一致的,不会存在跃变的情况。
该假设能保证可靠负样本是那些远离P集合中的所有样本。为此,很多人针对相似度(也就是距离)的衡量开展了各种研究。
Part 3. PU Learning的评估指标
传统二分类问题具有明确的0-1标签,很自然能计算准确率、召回率、F1值等标准评估指标。但在PU Learning问题中,该如何计算呢?
此时,我们就可以根据该指标评估PU问题的模型效果。
接下来,我们正式开始介绍PU Learning的基础方法(框架),通常可分为三类:
第一类是两阶段技术(Two-step PU Learning):先在未标记数据U中识别出一些可靠的负样本,然后在正样本P和这些可靠的负样本上进行监督学习。这是最常用的一种✅
第二类是有偏学习(Biased PU Learning):简单地把未标记样本U作为噪声很大的负样本来处理。
第三类是融入先验类别(Incorporation of the Class Prior):尝试给正样本P和未标记样本U赋予权重,并给出样本属于正标签的条件概率估计。
Part 4. 两阶段技术(Two-step PU Learning)
all the positive examples are similar to the labeled examples and that the negative examples are very different from them.
基于可分性和平滑性假设,所有正样本都与有标签样本相似,而与负样本不同。
为了绕过缺乏负标注的问题,two-stage策略首先挖掘出一些可靠的负例,再将问题转化为一个传统的监督和半监督学习问题。
整体流程一般可分解为以下3个步骤:
- step 1: 从U集合中识别出可靠负样本(Reliable Negative,RN)。
- step 2: 利用P集合和RN集合组成训练集,训练一个传统的二分类模型
- step 3: 根据某种策略,从迭代生成的多个模型中选择最优的模型。
在这个框架下,每一步又可以灵活选择各种方法。接下来,我们来详细解释每一步的细节。首先,可靠负样本的定义是什么?
基于平滑性假设,样本属性相似时,其标签也基本相同。换言之,可靠负样本就是那些与正样本相似度很低的样本。那么,问题的关键就是定义相似度,或者说距离(distance)。
4.1 识别可靠负样本
1)间谍技术(The Spy Technique)
2)1-DNF技术
1)间谍技术(The Spy Technique)
- step 1:从P中随机选择一些正样本S,放入U中作为间谍样本(spy)。此时样本集变为P-S和U+S。其中,从P中划分子集S的数量比例一般为15%。
- step 2:使用P-S作为正样本,U+S作为负样本,利用迭代的EM算法进行分类。初始化时,我们把所有无标签样本当作负类( �=0 ),训练一个分类器,对所有样本预测概率 ��(�=1) 。
- step 3:以spy样本分布的最小值作为阈值,U中所有低于这个阈值的样本认为是RN。
注意:spy样本需要有足够量,否则结果可信度低。
图 9 - 可靠负样本的选择算法
2)1-DNF技术
- step 1:获取PU数据中的所有特征,构成特征集合F。
- step 2:对于每个特征,如果其在P集合中的出现频次大于N集合,记该特征为正特征(Positive Feature,PF),所有满足该条件的特征组成一个PF集合。
- step 3:对U中的每个样本,如果其不包含PF集合中的任意一个特征,则将该样本加入RN。
4.2 训练分类器
在识别出可靠负样本RN后,我们来训练一个分类器,操作步骤描述如下:
# 样本准备:P 和 RN 组成训练集X_train; P给定标签1,RN给定标签0,组成训练集标签y_train# 用 X_train 和 y_train 训练逻辑回归模型 modelmodel.fit(X_train, y_train)# 用 model 对 Q 进行预测(分类)得到结果 probQ = U - RN # 无标签样本集U中剔除RNprob = model.predict(Q)# 找出 Q 中被判定为负的数据组成集合 Wpredict_label = np.where(prob < 0.5, 0, 1).T[0]negative_index = np.where(predict_label == 0)W = Q[negative_index]# 将 W 和 RN 合并作为新的 RN,同时将 W 从 Q 中排除RN = np.concatenate((RN, W)) # RN = RN + WQ = np.delete(Q, negative_index, axis=0) # Q = Q - W# 用新的 RN 和 P 组成新的 X_train,对应生成新的 y_train# 继续训练模型,扩充 RN,直至 W 为空集,循环结束。# 其中每次循环都会得到一个分类器 model ,加入模型集 model_list 中
4.3 最优模型选择
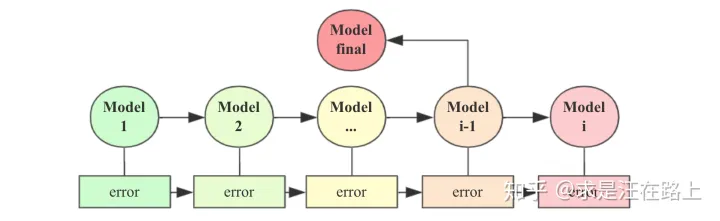
图 10 - 模型迭代和选择过程
3)投票(Vote)
对每轮迭代生成的模型model,进行加权组合成最终模型。
4)最后(Last)
直接选用最后一次迭代生成的分类器。
5) 假阴率(FNR > 5 %)
当超过已标注正样本的5%被错误预测为负类时,迭代停止。
我们用Python伪代码组织上述流程:
# 直接选用最后一次循环得到的分类器:final_model = model_list[-1]# 利用规则选出一个最佳分类器:# 用最后一次循环得到的分类器 S-last 对 P 进行分类。# 若分类结果中有超过8%条数据被判定为负,则选用第一次循环的分类器S-1。# 否则继续选用 S-last 作为最终分类器neg_predict = model_list[-1].predict(P)neg_predict = np.where(neg_predict < 0.5, 0, 1).T[0]if list(neg_predict).count(0) / neg_predict.shape[0] > 0.08:final_model = model_list[0]else:final_model = model_list[-1]# 对测试数据集进行分类result = final_model.predict(X_test)
Part 5. 有偏学习(Biased PU Learning)
有偏PU Learning的思想是,把无标签样本当作带有噪声的负样本。那么,该如何把噪声考虑进PU问题模型学习过程?可以采取以下方式:
- 噪声引起误分类,因此对错误分类的正样本置于更高的惩罚。
- 基于适合PU问题的评估指标来调整模型参数。
Part 6. 融入类别先验(Incorporation of the Class Prior)
在完全随机选择(SCAR)假设下,我们有以下几种方案:
Postprocessing:训练一个非传统分类器,再考虑修正输出概率。
Preprocessing:基于类先验来改变数据集,再训练模型。
6.2 预处理(Preprocessing)
思想:从PU数据中,基于类先验创造一个传统二分类模型学习的训练集。
1)Rebalancing Methods
2) Incorporation of the Label Probabilities
1)Rebalancing Methods
Part 7. 类别先验的估计方法
Part 8. Active Learning与PU Learning的对比
在《主动学习在风控中的应用(理论篇)》中,我们认识了Active Learning。很多人会疑惑,Active Learning与PU Learning之间有什么差异和相似点?
笔者认为,两者都是为了解决:针对有标签样本很少的情况,如何去训练一个二分类模型?
在Active Learning中,专家会多次标注,逐渐扩充L(Labeled)集合,active learner则会在多次学习L集合(包含正负样本)时不停提升自己的性能,我们称之为LU setting。在打标过程中,其有以下特点:
- 选择策略:在从U集合中选择样本时,选择策略与模型密切相关。例如,不确定性策略是选择模型最不确定的样本进行标注。
- L集合产物:在模型迭代过程中,积累的L集合包括P(Positive)和N(Negative),但其没有考虑到负样本的标注实际并不可靠这一问题。
- 人机交互:对人的依赖严重,需要人和模型之间交互频繁。
在PU Learning中,同样需要借助人工打标,Learner则在每次迭代的时候,基于PU数据进行学习,我们称之为PU setting。但差异点在于:
- 选择策略:在从U集合中选择样本时,选择策略与模型相关性低,主要依赖于样本自身之间的差异。例如,1-DNF技术致力于寻找正负样本显著差异的强特征集合。
- L集合产物:积累的L集合只包括P(Positive)。在Two-step PU Learning中,可靠负样本RN只是在模型迭代过程中的一个虚拟产物,我们总是认为负样本的标签是不可靠的。
- 人机交互:依赖相对较少。作为半监督学习的一种,在初始化后,可以依赖EM算法自动迭代。
因此,如何将两者结合起来,服务于实际业务场景是一个有趣的命题。
Part 9. 总结
本文系统介绍了PU Learning的相关理论,包括基本概念、操作流程、基础假设,以及与主动学习之间的对比。
下一篇中,将会介绍一些PU Learning的应用案例。
致谢
感谢参考资料的作者带给我的启发。本文尚有理解不当之处,在此抛砖引玉。
版权声明
欢迎转载分享,请在文章中注明作者和原文链接,感谢您对知识的尊重和对本文的肯定。
原文作者:求是汪在路上(知乎ID)
原文链接:https://zhuanlan.zhihu.com/p/98887617
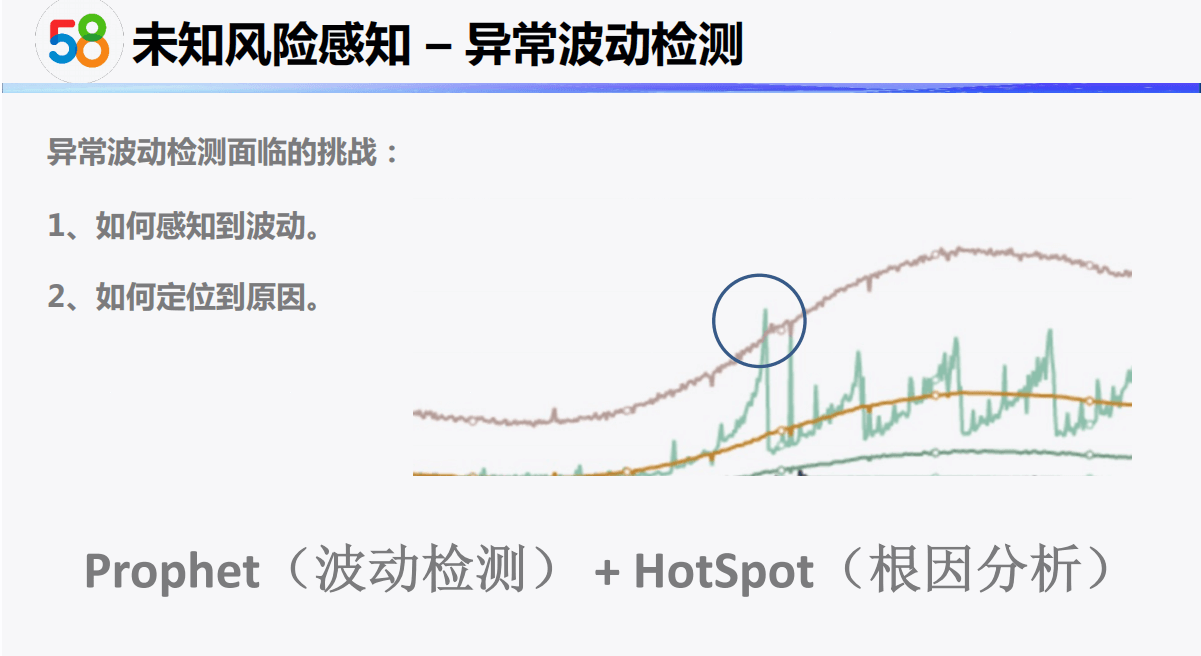
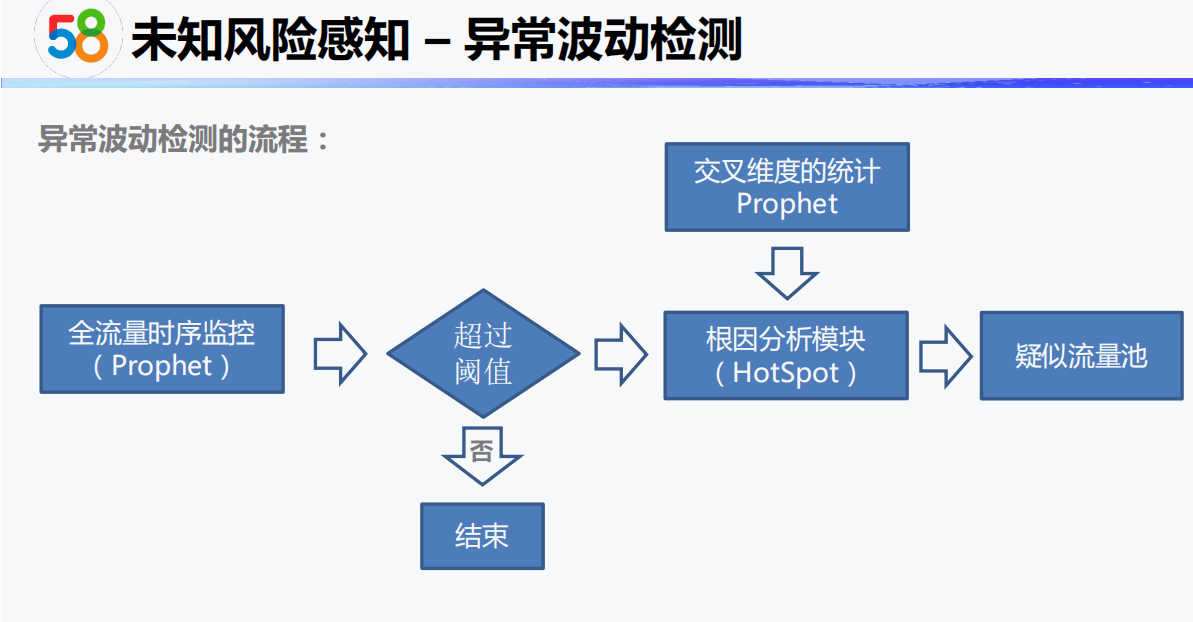
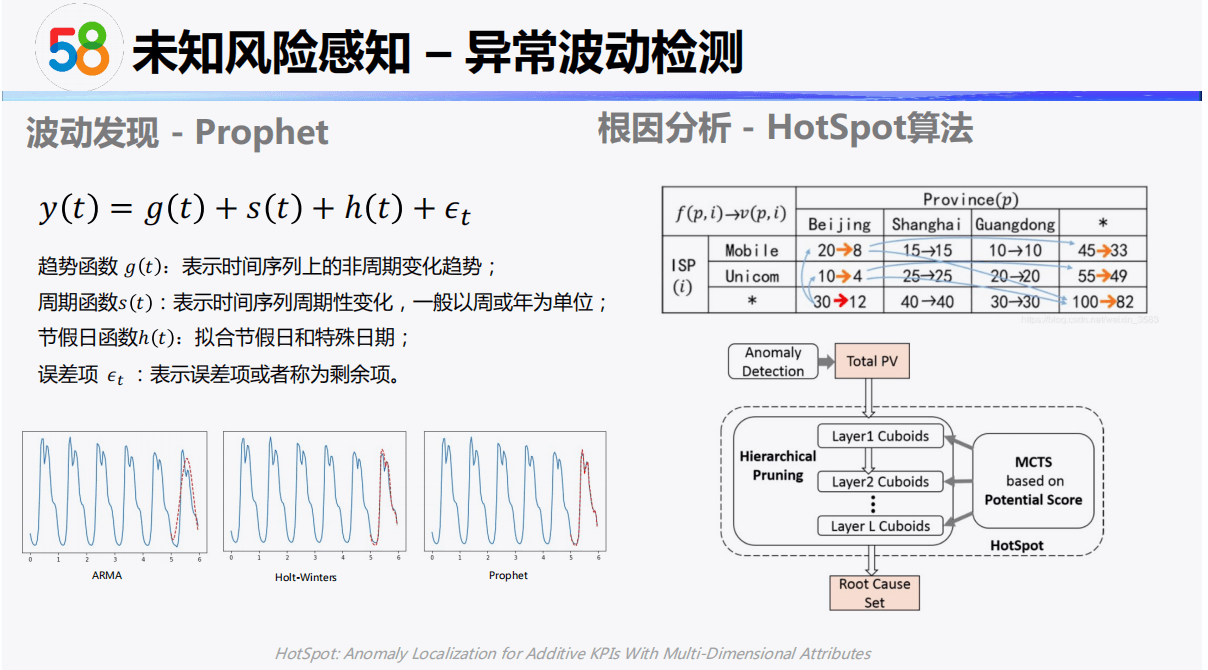
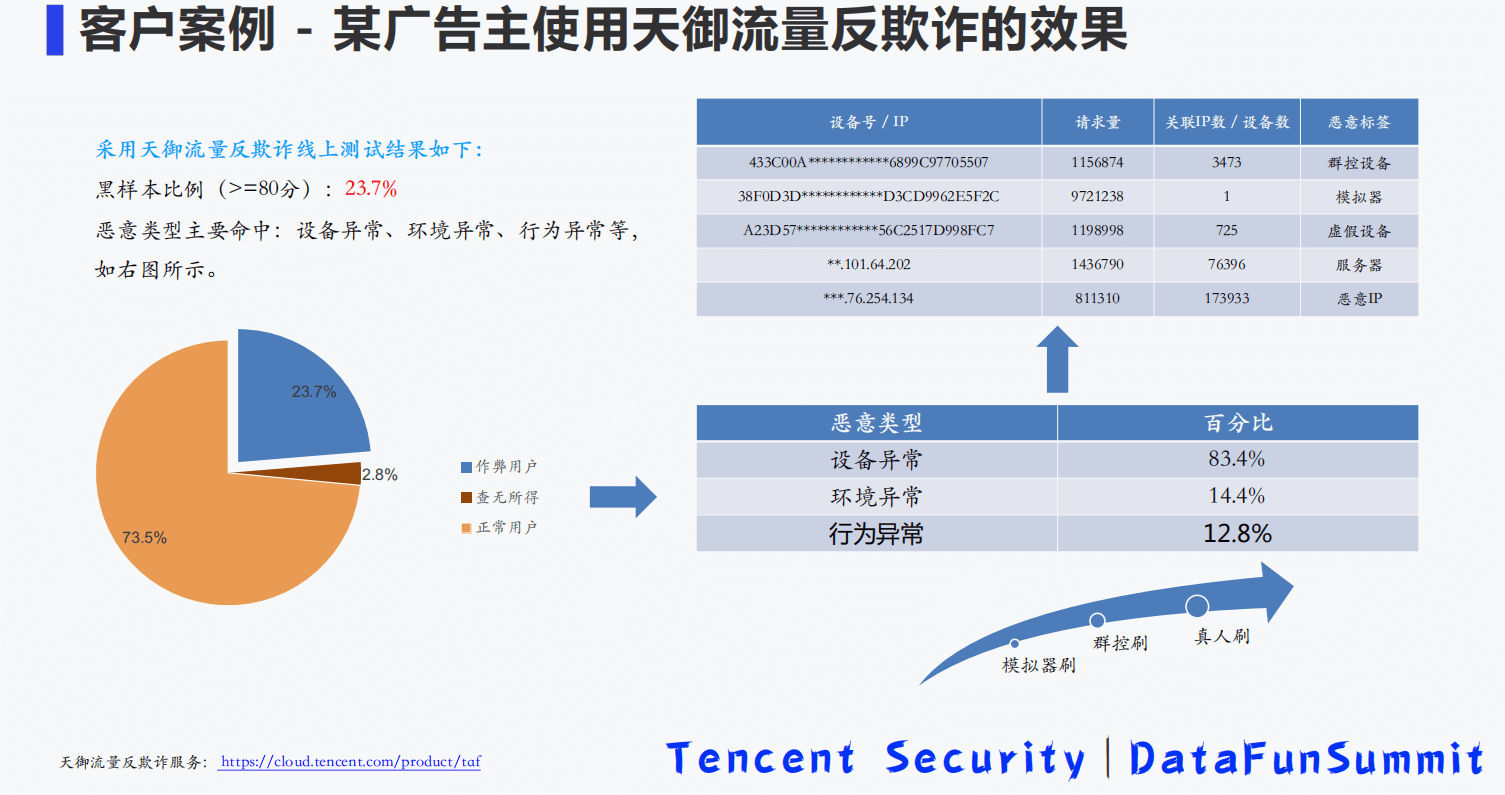
2-3 DataFunSummit-智能风控技术峰会分享-龚灿-20210515

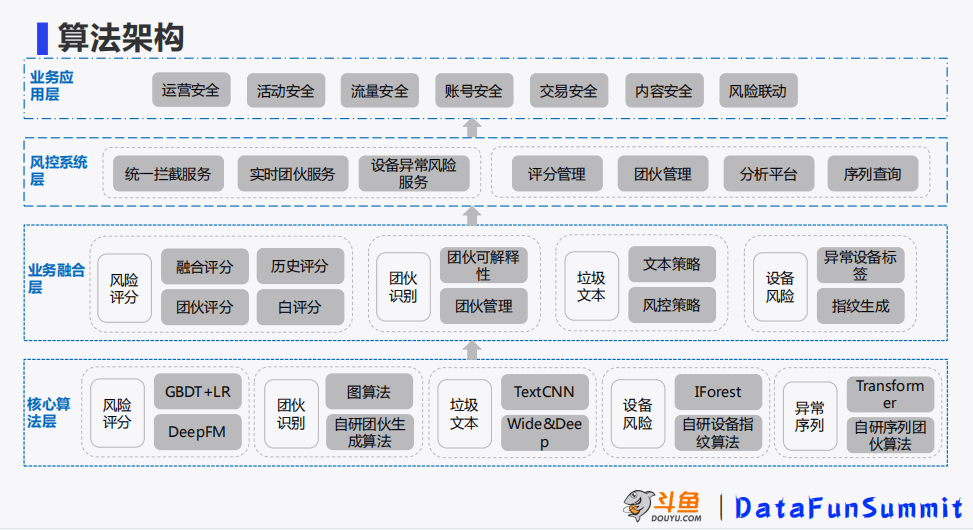

1-2 DataFunSummit-智能风控技术峰会-JDT
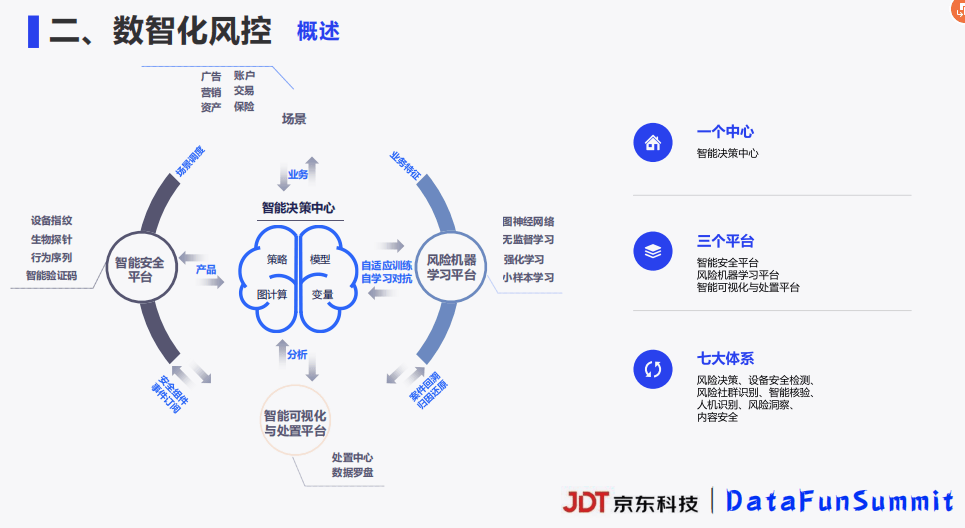
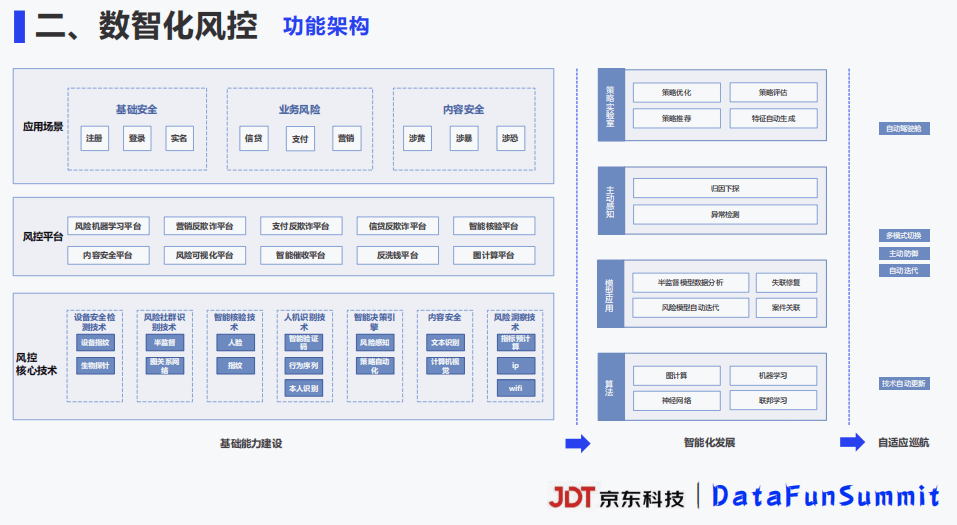
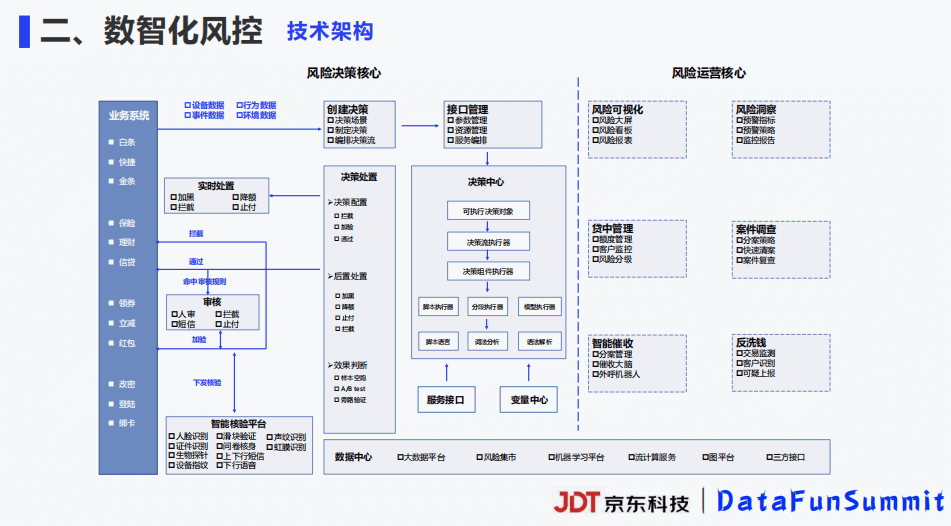
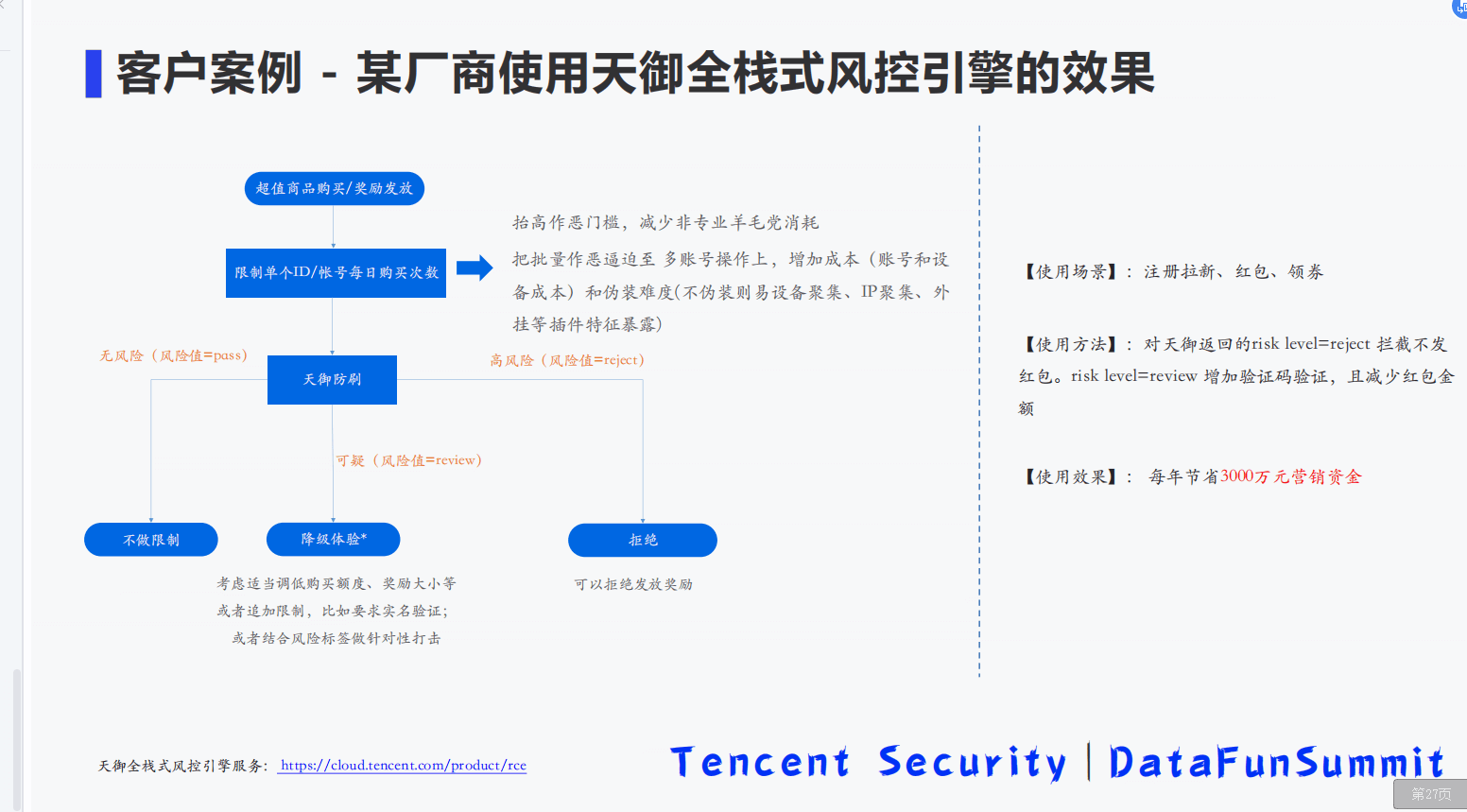
9-2 基于全栈式实时风控引擎的流量反作弊平台建设.pdf