决策树（用于分类预测）

决策树算法总结
一、简介
决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。 数据挖掘中决策树是一种经常要用到的技术，可以用于分析数据，同样也可以用来作预测（就像上面的银行官员用他来预测贷款风险）。
从数据产生决策树的机器学习技术叫做决策树学习, 通俗说就是决策树。
一个决策树包含三种类型的节点： 1.决策节点——通常用矩形框来表式 2.机会节点——通常用圆圈来表式 3.终结点——通常用三角形来表示
决策树学习也是资料探勘中一个普通的方法。在这里，每个决策树都表述了一种树型结构，它由它的分支来对该类型的对象依靠属性进行分类。每个决策树可以依靠对源数据库的分割进行数据测试。这个过程可以递归式的对树进行修剪。 当不能再进行分割或一个单独的类可以被应用于某一分支时，递归过程就完成了。另外，随机森林分类器将许多决策树结合起来以提升分类的正确率。
二、决策树算法
1.ID3算法
ID3算法是一个由Ross Quinlan发明的用于决策树的算法。这个算法便是建立在上述所介绍的奥卡姆剃刀的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。尽管如此，该算法也不是总是生成最小的树形结构，而是一个启发式算法。
汤姆.米歇尔《机器学习》中对ID3算法的描述：

ID3算法思想描述：（个人总结 仅供参考）
a.对当前例子集合，计算属性的信息增益；
b.选择信息增益最大的属性Ai(关于信息增益后面会有详细叙述)
c.把在Ai处取值相同的例子归于同于子集，Ai取几个值就得几个子集
d.对依次对每种取值情况下的子集,递归调用建树算法，即返回a，
e.若子集只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处。

2.最佳分类属性
判断测试哪个属性为最佳的分类属性是ID3算法的核心问题，那么这里就要介绍两个比较重要的概念：信息增益的度量标准：熵和信息增益Gain(S,A)
以下为《机器学习》和援引处的内容 有修改
1）信息增益的度量标准：熵
为了精确地定义信息增益，我们先定义信息论中广泛使用的一个度量标准，称为熵（entropy），它刻画了任意样例集的纯度（purity）。给定包含关于某个目标概念的正反样例的样例集S，那么S相对这个布尔型分类的熵为：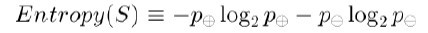

上述公式中，p+代表正样例，比如在本文开头第二个例子中p+则意味着去打羽毛球，而p-则代表反样例，不去打球(在有关熵的所有计算中我们定义0log0为0)。
相关代码实现：（代码有些晦涩难懂，如欲详加了解 请看：http://blog.csdn.net/yangliuy/article/details/7322015 里面有ID3完整的代码）

//根据具体属性和值来计算熵
double ComputeEntropy(vector > remain_state, string attribute, string value,bool ifparent){
vector count (2,0);
unsigned int i,j;
bool done_flag = false;//哨兵值
for(j = 1; j < MAXLEN; j++){
if(done_flag) break;
if(!attribute_row[j].compare(attribute)){
for(i = 1; i < remain_state.size(); i++){
if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){//ifparent记录是否算父节点
if(!remain_state[i][MAXLEN - 1].compare(yes)){
count[0]++;
}
else count[1]++;
}
}
done_flag = true;
}
}
if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例
//具体计算熵 根据[+count[0],-count[1]],log2为底通过换底公式换成自然数底数
double sum = count[0] + count[1];
double entropy = -count[0]/sumlog(count[0]/sum)/log(2.0) - count[1]/sumlog(count[1]/sum)/log(2.0);
return entropy;
}

举例来说，假设S是一个关于布尔概念的有14个样例的集合，它包括9个正例和5个反例（我们采用记号[9+，5-]来概括这样的数据样例），那么S相对于这个布尔样例的熵为：
Entropy（[9+，5-]）=-（9/14）log2（9/14）-（5/14）log2（5/14）=0.940。
注意，如果S的所有成员属于同一类，Entropy(S)=0，例如，如果所有的成员是正的（p+=1），那么p-就是0，于是Entropy（S）=-1log2（1）-（0）log2（0）=0； 另外S的正反样例数量相等，Entropy(S)=1；S的正反样例数量不等，熵介于0，1之间，如下图所示：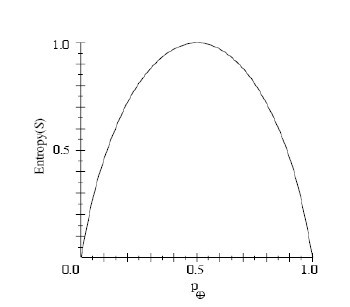

信息论中对熵的一种解释，熵确定了要编码集合S中任意成员的分类所需要的最少二进制位数。更一般地，如果目标属性具有c个不同的值，那么S相对于c个状态的分类的熵定义为：

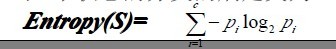
其中pi是S属于类别i的比例，需要注意的是底数仍然为2，原因熵是以二进制位的个数来度量编码长度，同时注意，如果目标属性具有c个可能值，那么熵最大可能为log2（c）。

2）信息增益Gain(S,A)定义和信息增益度量期望的熵降低
已经有了熵作为衡量训练样例集合纯度的标准，现在可以定义属性分类训练数据的效力的度量标准。这个标准被称为“信息增益（information gain）”。简单的说，一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低(或者说，样本按照某属性划分时造成熵减少的期望,个人结合前面理解，总结为用来衡量给定的属性区分训练样例的能力)。更精确地讲，一个属性A相对样例集合S的信息增益Gain(S,A)被定义为：

其中 Values(A)是属性A所有可能值的集合，Sv是S中属性A的值为v的子集，注意上式第一项就是原集合S的熵，第二项是用A分类S后的熵的期望值，第二项描述的期望熵就是每个子集的熵的加权和，权值为属性Sv的样例占原始样例S的比例|Sv|/|S|,所以Gain(S,A)是由于知道属性A的值而导致的期望熵减少，换句话来讲，Gain(S,A)是由于给定属性A的值而得到的关于目标函数值的信息。当对S的一个任意成员的目标值编码时，Gain(S,A)的值是在知道属性A的值后可以节省的二进制位数。
那么综上，我们就可以得出两个基本公式：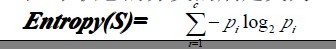


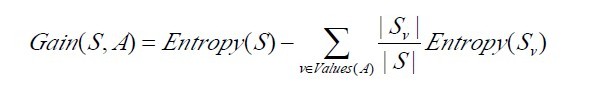
从中可以看出第一个Entropy(S)是熵定义，第二个则是信息增益Gain(S,A)的定义，而Gain(S,A)由第一个Entropy(S)计算出
下面仍然以《机器学习》一书中叙述的内容举例
假定S是一套有关天气的训练样例，描述它的属性包括可能是具有Weak和Strong两个值的Wind。像前面一样，假定S包含14个样例，[9+，5-]。在这14个样例中，假定正例中的6个和反例中的2个有Wind =Weak，其他的有Wind=Strong。由于按照属性Wind分类14个样例得到的信息增益可以计算如下。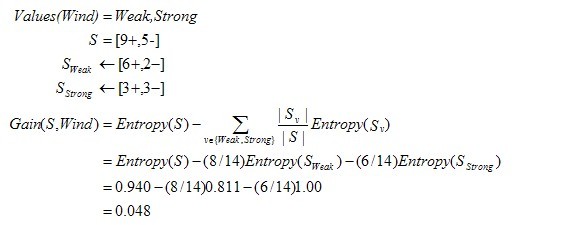

信息增益正是ID3算法增长树的每一步中选取最佳属性的度量标准下图（网上拷下可惜没有清晰版） 计算了两个不同属性：湿度（humidity）和风力（wind）的信息增益，以便决定对于训练样例哪一个属性更好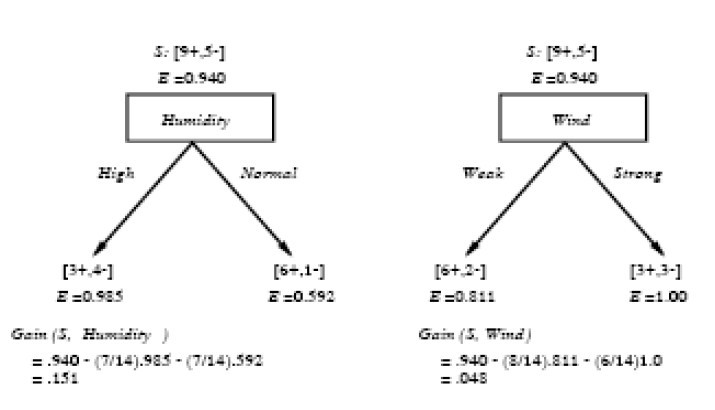

通过以上的计算，相对于目标，Humidity比Wind有更大的信息增益
下图仍摘取自《机器学习》 是ID3第一步后形成的部分决策树 其中经比较OutLook的信息增益最大 选作root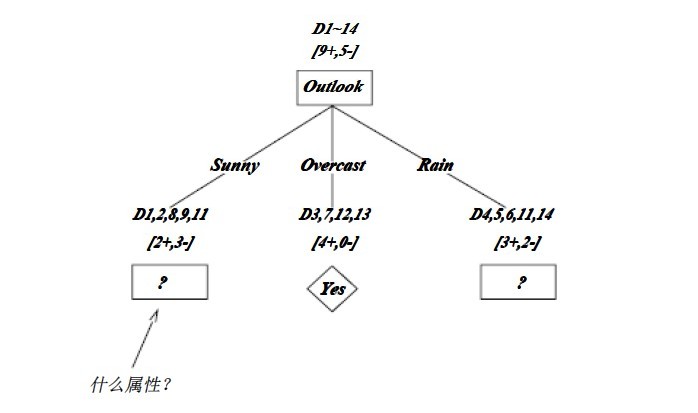

上图中分支Overcast的所有样例都是正例，所以成为目标分类为Yes的叶结点。另两个结点将被进一步展开，方法是按照新的样例子集选取信息增益最高的属性。
以上完整代码参见http://blog.csdn.net/yangliuy/article/details/7322015
*3.另一种决策树算法C4.5
这里仅作简单介绍
1）概览：
由于ID3算法在实际应用中存在一些问题，于是Quilan提出了C4.5算法，严格上说C4.5只能是ID3的一个改进算法。
C4.5算法继承了ID3算法的优点，并在以下几方面对ID3算法进行了改进：

• 用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；有关信息增益率的定义可以参考栾丽华和吉根林的论文《决策树分类技术研究》1.2节。
• 在树构造过程中进行剪枝；
• 能够完成对连续属性的离散化处理；
• 能够对不完整数据进行处理。

C4.5算法有如下优点：产生的分类规则易于理解，准确率较高。其缺点是：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。
2)主要步骤：
a. 读取文件信息，统计数目
b. 建立决策树

• 如果样本集为空，则生成一个信息数目都为0的树节点返回
• 如果样本均为同一类别，则生成一个叶子节点返回
• 计算节点正负样本的数目
• 如果属性值只有那个类别的属性，则生成一个叶子节点，并赋值类型索引
• 如果以上都不是，则选择一个增益率最大的属性（连续属性要用增益率离散化），按那个属性的取值情况从新定义样本集和属性集，建造相关子树

c. 事后剪枝（采用悲观错误率估算）
d. 输出决策树
e. 移除决策时
主要重点有：信息增益率的计算、事后剪枝使用悲观错误率衡量、树的建造（分治思想）
信息增益率的计算相关公式：

• 
• 
• 

• 

  
  
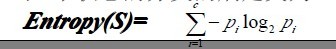
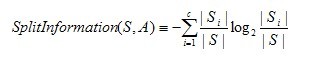
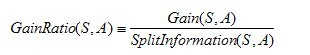
  悲观错误剪枝PEP算法：（以下知识简单引导一下 如需详加了解 请阅览相关剪枝算法的书籍 ，笔者没有对此作深入的研究，so不做细讲）
  所用来剪枝的度量的基本思想可以概述为以下几点：

• 假设训练数据集生成原始树为T，某一叶子结点的实例个数为nt(t为右下标，以下同)，其中错误分类的个数为et；

• 我们定义训练数据集的误差率如下公式所示：

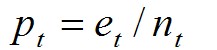
由于训练数据集既用来生成决策树又用来修剪树，所以是有偏倚的，利用它来修剪的决策树树并不是最精确，最好的；

• 为此，Quinlan在误差估计度量中增加了连续性校正，将误差率的公式修改为如下公式所示

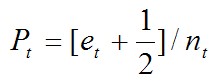
• 那么，同样的，我们假设s为树T的子树的其中一个子节点，则该子树的叶子结点的个数为ls ，Tt的分类误差率如下公式所示:

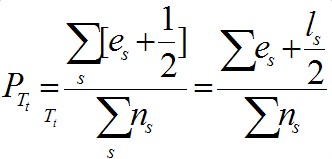
在定量的分析中，为简单起见，我们用误差总数取代上面误差率的表示，即有公式: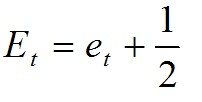

那么，对于子树Tt，它的分类误差总数如下公式所示：