格子大法与换入换出分析

来源：https://mp.weixin.qq.com/s/K5KzOPlLN-KklrTv_SOoIg

做风控策略的时候，大家应该都听说过这两个词。格子法就是用画列联表的方式来进行交叉变量分析，一般用于两个评分之间的交叉；换入换出又叫Swap Set分析，用于对比新旧策略的差异，详细介绍可以参看求是汪知乎：《利用Swap Set分析风控模型更替的影响》。
本文是我前几天在番茄的一份培训课件中看到的案例，讲解的是用格子法对白名单筛选策略进行调整，并通过换入换出来分析策略调整的影响。

目录
一、格子大法
二、换入换出
三、其它

一、格子大法
首先，通过一些硬规则和软规则筛选出白名单客群，并剔除近60天人行查询客群，选定B卡分>640分为cutoff，得到老白名单。现需要加入一个大额现金贷准入评分，来替换软规则，通过换出高风险客群换入低风险客群的方法来达到增加白名单范围的目的。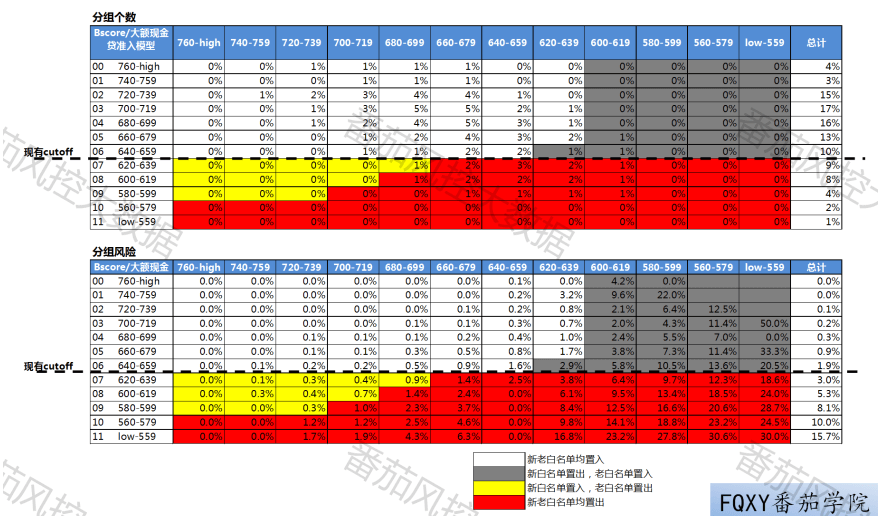

如上图，图中第一个表格是分数交叉后的个数比例情况，第二个表格是分数交叉后的风险情况。以B卡分大于640分对应的边际风险1.9%进行换入换出。图中黄色部分为新白名单换入的部分，灰色部分为新白名单换出的部分。因此新白名单应为白色区域+黄色区域。新的策略如下：
(Bscore>660&大额现金分>620)且(Bscore介于640和659之间&大额现金分>640)且(Bscore介于620和639之间&大额现金分>680)且(Bscore介于600和619之间&大额现金分>700)且(Bscore介于580和599之间&大额现金分>720)
在实际操作过程中，有一部分客户会被Bscore这一节点之前的硬规则拒绝，所以会导致没有Bscore分，这是上面没有考虑到的。这里选的1.9%作为风险容忍线，实际情况中这个取值可以根据公司的风险偏好来设定，考虑到评分缺失的客户，阈值可以适当更低一点，留出一些风险缓释垫以确保策略效果和线上效果更为接近。

二、换入换出
根据上图中的新旧白名单切分后的结果，统计相应的客户数量、风险表现，对比新旧白名单的效果(实际与上图有些不符，上图换出3%的客户换入1%的客户)。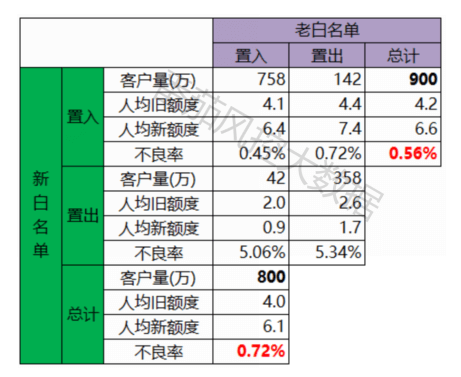

旧白名单：800万客户，不良率0.72%；
新白名单：900万客户，不良率0.56%。
新白名单较于旧白名单，在扩充白名单客户数量的同时，降低了风险，因此新白名单效果更好。
实际工作中，对于老模型拒绝的客户，往往并不知道其风险表现，也就是上图中cutoff下面的部分。这部分可以通过拒绝推断或者只打分不决策的方式来获取样本的表现，以便评估模型在整体客群上的效果。拒绝推断相关的介绍可以参考求是汪的另一篇文章：《风控建模中的样本偏差与拒绝推断》

三、其它
这部分是我在实际工作中遇到的一个问题，当时和几位同行朋友也进行了交流，有一些收获，写出来和各位交流探讨一下。
模型上线后(A分数)，对每月的线上样本进行监控，看KS指标的变化情况。另外，由于新接了一个外部数据分(B分数)，还没有用于作策略，因此就把这个分数在线上样本上的ks也看了下，结果发现外部数据分每个月的ks都比自有模型好。这种情况比较少见，于是就有一个疑问：是否这个外部数据分就比自建模型的效果好？
一般这种情况不多见的原因是，自建模型是融合了外部数据、用户数据，选用历史进件样本进行建模，而外部数据可能是基于某一类数据进行建模，所以效果上应该是自建模型的效果更好。线上样本A分数的ks比B低，说明在线上样本上B的区分度更好，下图中红色虚线右半部分。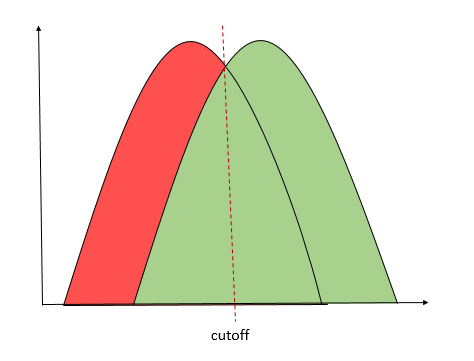

当然，在线上样本上区分度好，并不能说明在全量样本上区分度也更好。如果反过来，用B分做决策，A分空跑，那么如果B分换出(A分换入)的客户比换入(A分换出)的客户风险表现低，那么用B作主模型决策的表现会比原来差。因此有两种做法：
1.进行拒绝推断。预估全量样本上两个分数的表现。
2.两个分数做交叉选择。
拒绝推断，除了常用的那些方法之外，实际操作中还有一个方法：把自有模型拒绝外部分通过的样本按照一定系数分给外部分的各个等级，预估用外部分做决策时的风险情况。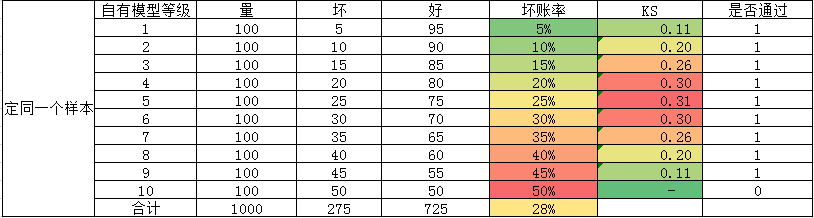


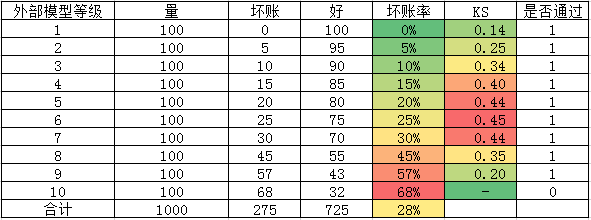
上图分别是同一批样本上，自有模型和外部数据分对应的各评分段的风险情况，可以看到自有模型的ks比外部分低，然后模拟用外部数据分作为主模型，通过率及坏账的变化。

in_in：自有模型和外部分都通过
swap_in：外部分通过，自有模型拒绝
上图中黄色的一列，为坏账预估系数，需要结合测试数据和经验来拍一个值。然后就可以得到外部数据分通过样本上做cutoff对应的通过率和坏账。但是这里是只对外部分通过、自有模型拒绝的样本进行了推断，也就是基于外部分通过的样本进行模拟，外部分拒绝的样本其实表现仍然未知。
所以如果出现线上样本的外部数据分区分度更好的情况下，用外部数据分来作主模型的话会是什么效果，这是值得深入思考的一个问题。在此抛转引玉，各位可以思考一下。