参考来源：
【1】校园卡数据来源及介绍：https://github.com/Nicole456/Analysis-of-students-consumption-behavior-on-campus
【2】校园卡数据分析-背景来源：https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650189560&idx=1&sn=e8bc535285990682fce507c1c58c059d&chksm=8823893cbf54002a51e9b0a0bf43df6d42dd08c5a9a9323d689bf8e879984ce0dced4891af0a&scene=21#wechat_redirect
【3】关联分析算法Apriori介绍：https://www.cnblogs.com/codeshell/p/14113600.html
【4】Apriori、FP-growth算法一步一步实现：https://www.cnblogs.com/lsqin/p/9342926.html
【5】FP-growth图解案例：https://www.cnblogs.com/datahunter/p/3903413.html
【6】频繁模式挖掘中Apriori、FP-Growth和Eclat算法的实现和对比：https://www.cnblogs.com/infaraway/p/6774521.html
【7】校园卡数据-基于SynchroTrap+LPA算法的团伙账户挖掘：https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650189651&idx=1&sn=4d152af90a40a3d78ad5277c3060e1ff&chksm=88238897bf540181716606d8c7dbda8ff51c3a6d580e89dd3c7e1e31cfd2bb60a1647e357b7a&scene=21#wechat_redirect

【总的资源来源】
https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650192912&idx=1&sn=59a50b4d1847aa818d7da16a74c1a69e&chksm=88239bd4bf5412c2f591d1a80714d3be3c64b86fee653e1ec3f2ae4d3f6a5d170d94ff65cae8&scene=21&key=6a16a961311a0ee0c5b03ffe3e15c64f3c7f35aa6345065b30b7650ef4a046fc3d474000e8a319bba625990822d5eb4e4f8177c9beb448929f6fe1bcb04e01a6751d1b909647caa7df0f20cc7fbc6e885ca3f499aed406816e53ab49421b67d0205d37ad2ac3c0f9e853df92420b119017a55e05cc4e89aa9c8938b10c464374&ascene=15&uin=MjcyNjQ5NTAxOQ%3D%3D&devicetype=Windows+10+x64&version=63080029&lang=zh_CN&session_us=gh_115024bacc7b&exportkey=n_ChQIAhIQHU0UYiKK0qYumVA9wwfofBLvAQIE97dBBAEAAAAAAMIhCqwrYz4AAAAOpnltbLcz9gKNyK89dVj0Ar0ksCw%2BoEDpDnqVo%2BXk7ZI644%2BrSK4ep03FKOKSeEXS1cN13HyadeXQutIlwrv5bpR%2FLZVCLfj599w8e%2Fz764aHB5FeLgrCHhjEJO3g7NRUBbMCwVjJxONDGtvwJf55qDAEtuLII2zr747RW6RaB7JFbCzEa3b2ExtWRpEOojzB1h0KjIoJZ617Zc4tchd8VVjVsMWUboM4jTEUsv3QTRYN%2BsYjSW9g16qS9mVI7%2FE%2BhFq47eQ2D%2F2wTxDTfj1tPBh%2BeZo9P9vn&acctmode=0&pass_ticket=uhzOU1KvGRbjCs7trc2RSV52Gn5Yppw6C9yO1KV%2FJJUjkQJLPzTIjyQ3EBjw1oegIIJ7gy5pqjJQdbq3jepFNw%3D%3D&wx_header=1&fontgear=2

【1】校园卡数据来源及介绍

数据下载：https://github.com/Nicole456/Analysis-of-students-consumption-behavior-on-campus

Description

基于国内某高校校园一卡通系统一个月的运行数据，使用数据分析和建模的方法，挖掘数据中所蕴含的信息，分析学生在校园内的学习生活行为

Goal

  1. 分析学生的消费行为和食堂的运营状况，为食堂运营提供建议。

  2. 构建学生消费细分模型，为学校判定学生的经济状况提供参考意见。

    Tasks

    数据导入与预处理

    • 理解字段含义,探查数据质量并进行缺失值和异常值等方面的必要处理

    • 将 学生个人信息数据表与消费记录数据表建立关联；将 学生个人信息数据与门禁进出记录建立关联

      食堂就餐行为分析

    • 绘制各食堂就餐人次的占比饼图，分析学生早中晚餐的就餐地点是否有显著差别

    • 通过食堂刷卡记录，分别绘制工作日和非工作日食堂就餐时间曲线图，分析食堂早中晚餐的就餐峰值

    • 根据分析的结果，为食堂的运营提供建议

      学生消费行为分析

    • 根据学生的整体校园消费数据，计算本月人均刷卡频次和人均消费额，并选择 3 个专业，分析不同专业间不同性别学生群体的消费特点

    • 根据学生的整体校园消费行为，选择合适的特征，构建聚类模型，分析每一类学生群体的消费特点
    • 通过对低消费学生群体的行为进行分析，探讨是否存在某些特征，能为学校助学金评定提供参考

    • 【2】校园卡数据分析-背景来源

      故事从校园一卡通开始，校园一卡通是集身份认证、金融消费、数据共享等多项功能于一体的信息集成系统，也就是学生卡。积累了大量的历史记录，其中蕴含着学生的消费行为和财务状况等信息。是一个数据分析比赛的数据，很多报告都是从消费金额、消费地点、消费时间等角度分析，比较常规。但是数据，其实还可以更有趣。
      本次使用南京理工一卡通的消费明细，我会从一个全新的角度出发，挖掘其中的情侣、基友、渣男、单身狗，大家可以把类似的方法扩展到风控领域使用，这种挖掘思路可以用到反欺诈、反舞弊等场景，思路比较新颖，具有较大的研究价值。

      结果解读

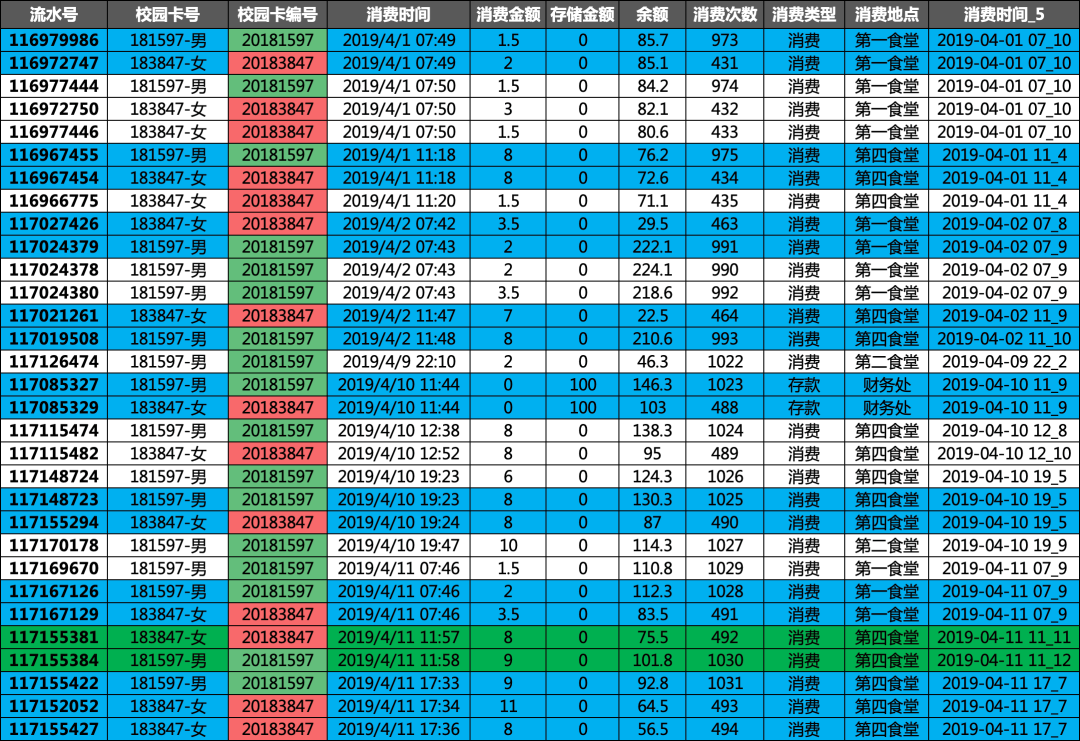
      上面挖掘的，都是汇总数据，为了更加具体，我们挑一对男女的消费明细来看看，这一对同学，一个月内出现了44次的关联，基本上每天都一起出入了，并且是男女组合。
      (‘181597-男’,’183847-女’)：44
      2019/4/1 07:49 男生女生一起去吃早餐，男生吃了3块钱的，女生吃了6.5的，在第一食堂，多年后可能还能记起这一顿早餐
      2019/4/1 11:18 男生女生一起去吃午饭，男生吃了8块钱的，女生也吃了8的，估计吃的饺子，或者是麻辣烫，这次在第四食堂，可能是上课的教室就在这附近
      2019/4/2 07:42男生女生一起去吃早餐，男生吃了7.5块钱的，女生吃了3.5的，估计昨天点多了，没吃完，今天少吃点
      2019/4/17 20:43 估计刚刚约会好了，在红太阳超市，女生估计买了个酸奶，男生饿了，买个个老坛酸菜牛肉面，买完，操场上一个大大的拥抱，各自回宿舍了，带着满满的甜蜜和力量，大学的美好，不过如此了·····
      ·······
      基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图1

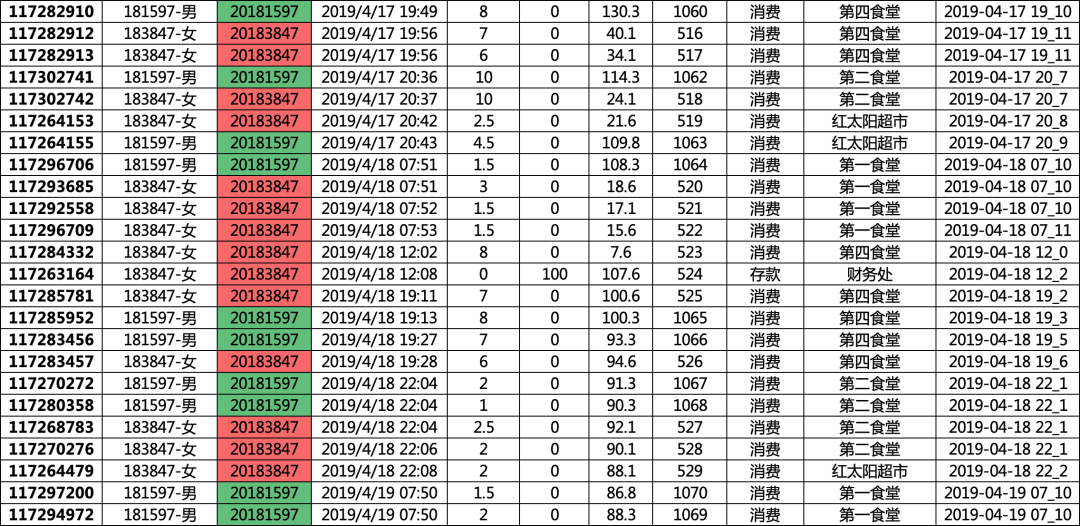
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图2
数据挖掘，我们不应该机械冰冷，应该通过数据，洞察后面的细节与故事，有时候，数据挖掘，是多么美妙的故事呢。
除了这一对，还有很多对的情侣，也是类似的生活轨迹。
通过分析，我们也发现两个渣男，啊呸，打死算了，细节我就不看了，你们去看

  1. ('180624-男', '181013-女'): 36('180624-男', '181042-女'): 37
  2. ('180780-女', '181461-男'): 38('180856-女', '181461-男'): 34

还有我们挖掘的数据，剔除部分，有大量的单身狗的含量，没有人和他一起吃饭
更多的是，基友和闺蜜，多元的

时空关联规则的影子账户挖掘代码

  1. # -*- coding: utf-8 -*-
  4. # 数据读取
  5. import numpy as np
  6. import pandas as pd
  7. import os
  9. pd.set_option('display.max_columns', None)
  10. os.chdir("/Users\yingtao.xiang\Downloads\Analysis-of-students-consumption-behavior-on-campus-master\Analysis-of-students-consumption-behavior-on-campus-master\data")
  11. data1 = pd.read_csv("data1.csv", encoding="gbk")
  12. data2 = pd.read_csv("data2.csv", encoding="gbk")
  13. data3 = pd.read_csv("data3.csv", encoding="gbk")
  15. data1.columns = ['序号', '校园卡号', '性别', '专业名称', '门禁卡号']
  16. data2.columns = ['流水号', '校园卡号', '校园卡编号', '消费时间', '消费金额', '存储金额', '余额', '消费次数', '消费类型', '消费项目编码', '消费项目序列号', '消费操作编码', '操作编码', '消费地点']
  17. data3.columns = ['序号', '门禁卡号', '进出时间', '进出地点', '是否通过', '描述']
  19. print(data1.head(3))
  20. # 序号    校园卡号 性别    专业名称      门禁卡号
  21. # 0   1  180001  男  18国际金融  19762330
  22. # 1   2  180002  男  18国际金融  20521594
  23. # 2   3  180003  男  18国际金融  20513946
  25. print(data2.head(3))
  26. # 流水号      校园卡号     校园卡编号             消费时间  消费金额  存储金额     余额  消费次数  \
  27. # 0  117342773  181316-女  20181316  2019/4/20 20:17   3.0   0.0  186.1   818   
  28. # 1  117344766  181316-女  20181316   2019/4/20 8:47   0.5   0.0  199.5   814   
  29. # 2  117346258  181316-女  20181316   2019/4/22 7:27   0.5   0.0  183.1   820   
  31. #   消费类型  消费项目编码 消费项目序列号  消费操作编码  操作编码  消费地点 性别  
  32. # 0   消费      49     NaN     NaN   235  第一食堂  女  
  33. # 1   消费      63     NaN     NaN    27  第二食堂  女  
  34. # 2   消费      63     NaN     NaN    27  第二食堂  女  
  36. print(data3.head(3))
  37. #  序号      门禁卡号           进出时间       进出地点  是否通过    描述
  38. # 0  1330906  25558880  2019/4/1 0:00  第六教学楼[进门]     1  允许通过
  39. # 1  1330907  18413143  2019/4/1 0:02  第六教学楼[出门]     1  允许通过
  40. # 2  1331384  11642752  2019/4/1 0:00    飞凤轩[进门]     1  允许通过
  43. # 数据处理~~~~~~~~~~~~~~~~~
  45. data2 = data2.merge(data1[['校园卡号','性别']],on='校园卡号')
  47. data2['校园卡号'] = data2['校园卡号'].apply(lambda x: str(x))+'-'+data2['性别'] # 校园卡号处理，加上性别
  49. # 时间格式调整,转换成比较标准的格式，方便后面的处理
  50. import datetime
  51. def st_pt(x):
  52.     #'2019/4/20 20:17'=>'2019-04-20 20:17:00'
  53.      return str(datetime.datetime.strptime(x, "%Y/%m/%d %H:%M"))
  55. # 时间离散化，每个五分钟一个类型
  56. def time_5(s):
  57.     #'2022-02-22 17:46:07'=>'2022-02-22 17_9'
  58.     a = str(round(int(s.split(':')[1])/5))
  59.     return s.split(':')[0]+'_'+a
  61. # 数据处理，处理成标准的格式
  62. df = data2
  63. df = df.sort_values(by='消费时间',ascending=True) 
  64. df['消费时间_F'] = df['消费时间'].apply(st_pt)  # 转换为标准时间
  65. df['消费时间_5'] = df['消费时间_F'].apply(time_5) # 每5分钟一个间隔，一个小时12个
  68. print(df.head(3))
  69. #              流水号      校园卡号     校园卡编号            消费时间  消费金额  存储金额     余额  消费次数  \
  70. # 57869  116925030  180641-女   2018641  2019/4/1 10:00   3.5   0.0  206.7   804   
  71. # 60120  116969953  181021-女  20181021  2019/4/1 10:00   2.0   0.0  127.9   512   
  72. # 63191  116969952  181036-女  20181036  2019/4/1 10:00   3.0   0.0   12.6   451   
  74. #       消费类型  消费项目编码 消费项目序列号  消费操作编码  操作编码   消费地点 性别               消费时间_F  \
  75. # 57869   消费     107     NaN     NaN   135  红太阳超市  女  2019-04-01 10:00:00   
  76. # 60120   消费      12     NaN     NaN   236   第一食堂  女  2019-04-01 10:00:00   
  77. # 63191   消费      12     NaN     NaN   236   第一食堂  女  2019-04-01 10:00:00   
  79. #                 消费时间_5  
  80. # 57869  2019-04-01 10_0  
  81. # 60120  2019-04-01 10_0  
  82. # 63191  2019-04-01 10_0  
  84. print(df['消费时间_5'].unique())
  85. print(pd.DataFrame(df['消费时间_5'].unique()).value_counts()) #打印出来 6176个唯一值
  87. all_list = []
  88. for v in df['消费时间_5'].unique():
  89.     one = df[df['消费时间_5']==v]['校园卡号'].unique().tolist()
  90.     all_list.append(one)
  93. # df[df['消费时间_5']==v]['校园卡号']
  94. # Out[47]: 
  95. # 211747    180104-女
  96. # 106417    180694-女
  97. # 106418    180694-女
  98. # 182463    180008-男
  99. # 3697      180826-女
  100. # 15368     182748-男
  101. # 76287     181202-女
  102. # 10412     181891-男
  103. # Name: 校园卡号, dtype: object
  105. # one
  106. # Out[49]: 
  107. # ['180104-女',
  108. #  '180694-女',
  109. #  '180008-男',
  110. #  '180826-女',
  111. #  '182748-男',
  112. #  '181202-女',
  113. #  '181891-男']
  116. print(len(all_list))#可以看到，有6176个时间片段，可以类比6176个订单
  117. # 6176
  119. all_list # 看看list长什么样子    
  120. # [['181735-女','180015-女'],['181058-男', '181374-男', '182044-女', '182581-女', '180052-女', '182729-男'],['181405-男','180078-男'],···]
  123. #数据保存起来
  124. df.to_csv('df.csv',header=True,index=False)
  127. # 关联规则挖掘~~~~~~~~~~~~~~
  129. #加载包，没有的自行安装
  130. #pip install efficient-apriori
  132. from efficient_apriori import apriori
  134. # Apriori 算法是一种发掘事物内在关联关系的算法，它可以加快关联分析的速度，从而让我们更有效的进行关联分析。
  136. # 关联分析 
  137. # 来源：https://www.cnblogs.com/codeshell/p/14113600.html
  138. # 关联分析用于发掘大规模数据集中的内在关系。
  139. # 关联分析一般要分析数据集中的频繁项集（frequent item sets）和关联规则（association rules）：
  140. # 频繁项集：是数据集中频繁项的集合，集合中可以有一项或多项物品。
  141. # 关联规则：暗示了两种物品之间可能存在很强的内在关系。
  143. itemsets, rules = apriori(all_list, min_support=0.005,  min_confidence=1)
  145. itemsets[2]
  146.  # ('183305-女', '183317-女'): 38,
  147.  # ('183308-女', '183317-女'): 42,
  148.  # ('183310-女', '183314-女'): 31,
  149.  # ('183315-女', '183324-女'): 32,
  150.  # ('183338-男', '183345-男'): 40,
  151.  # ('183343-男', '183980-女'): 44,
  152.  # ('183385-女', '183401-女'): 40,
  153.  # ('183386-女', '183409-女'): 34,
  154.  # ('183408-女', '183415-女'): 42,
  155.  # ('183414-女', '183418-女'): 41,
  156.  # ('183419-女', '183420-女'): 56,
  157.  # ('183419-女', '183422-女'): 59,
  158.  # ···
  159. len(itemsets[2]) # 一共有三百多对，我们下面挑一部分来分析
  160. # 378

我们分析用的是校园刷卡数据，这样的时序数据，随处可见
订单下单数据
领券明细数据
信用卡刷卡数据
····
非常多的这种数据，我们可以通过时序关联的方法挖掘出来其中的时空关系，从而确定多个有一致行动的用户，达到一起打击的目的。
当然，这种方法也是有缺陷的，有些相隔时间近但是不再同一个5min中内的，不会产生关联，其实有更先进的算法去解决，我们后面慢慢介绍，因为比较抽象。

【3】关联分析算法Apriori介绍

1，关联分析

关联分析用于发掘大规模数据集中的内在关系。
关联分析一般要分析数据集中的频繁项集（frequent item sets）和关联规则（association rules）：

  • 频繁项集：是数据集中频繁项的集合，集合中可以有一项或多项物品。
  • 关联规则：暗示了两种物品之间可能存在很强的内在关系。

假设，我们收集了一家商店的交易清单：

交易编号 购物清单
1 牛奶，面包
2 牛奶，面包，火腿
3 面包，火腿，可乐
4 火腿，可乐，方便面
5 面包，火腿，可乐，方便面

频繁项集是一些经常出现在一起的物品集合。比如：{牛奶，面包}，{火腿，方便面，可乐}都是频繁项集的例子。
项集中的物品，一般不考虑顺序关系。
关联规则意味着有人买了一种物品，还会买另一种物品。比如方便面->火腿，就是一种关联规则，表示如果买了方便面，还会买火腿。

2，三个重要概念

关联分析中有三个重要的概念，分别是：

  • 支持度
  • 可信度 / 置信度
  • 提升度

支持度
要进行关联分析，首先要寻找频繁项，也就是频繁出现的物品集。那么怎样才叫频繁呢？我们可以用支持度来衡量频繁。
支持度是针对项集来说的，一个项集的支持度就是该项集的记录占总记录的比例。通常可以定义一个最小支持度，从而只保留满足最小支持度的项集。
一个项集{A} 的支持度的定义如下：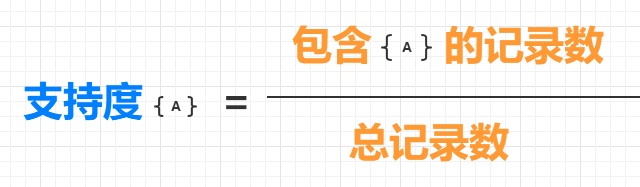
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图3
比如，在上面表格中的5 项记录中，{牛奶} 出现在了两条记录中，所以{牛奶} 的支持度为 2/5；而{面包，火腿} 出现在了三条记录中，所以{面包，火腿}的支持度为3/5。
可信度
可信度又叫置信度，它是针对关联规则来说的，比如{火腿}->{可乐}。
一个关联规则{A}->{B} 表示，如果购买了物品A，会有多大的概率购买物品B？它的可信度的定义如下：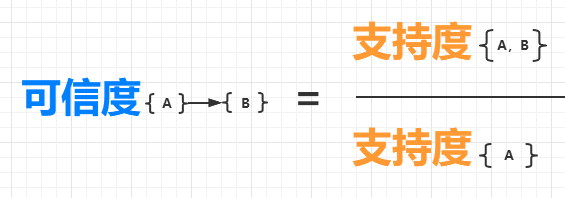
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图4
所以，在上面的表格中，{火腿，可乐} 的支持度是 3/5，{火腿} 的支持度是 4/5，所以{可乐}->{火腿} 的可信度为 3/5 除以 4/5，等于 0.75。这意味着，如果购买了火腿，有 75% 的可能性会购买可乐。
提升度
提升度也是针对关联规则来说的，它表示的是“如果购买物品A，会对购买物品B 的概率提升多少”。
一个关联规则{A}->{B} 的提升度的定义如下：
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图5
提升度会有三种情况：

  • 提升度{A}->{B} > 1：表示购买物品A 对购买物品B 的概率有提升。
  • 提升度{A}->{B} = 1：表示购买物品A 对购买物品B 的概率没有提升，也没有下降。
  • 提升度{A}->{B} < 1：表示购买物品A 对购买物品B 的概率有下降。

    3，如何寻找频繁项

    寻找频繁项的一个简单粗暴的方法是，对所有的物品进行排列组合，然后计算所有组合的支持度，这种算法也可以叫做穷举法。
    穷举法
    穷举法就是列出所有物品的组合，然后计算每种组合的支持度。
    比如，我们有一个物品集{0，1，2，3}，其中有四个物品，那么所有的物品组合如下：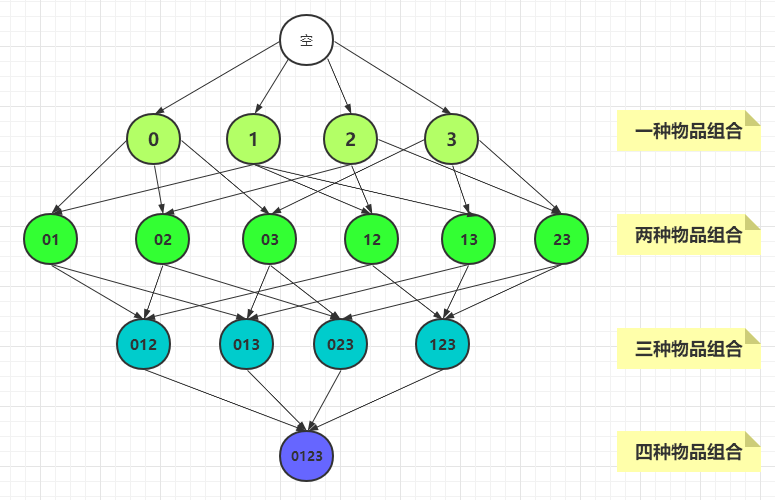
    基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图6
    从图中可以看到一共有15 种组合，计算每一种组合的支持度都需要遍历一遍所有的记录，检查每个记录中是否包含该组合。因此有多少种组合，就需要遍历多少遍记录，时间复杂度则会很大。
    可以总结出：包含N 种物品的数据集，共有 2N - 1 种组合。为了计算每种组合的支持度，则需要遍历 2N - 1 次记录。
    如果一个商店中有100 款商品，将会有1.26*1030 种组合，这是一个非常庞大的数字。而普通商店一般都会有成千上万的商品，那么组合数将大到无法计算。

    4，Apriori 算法

    为了降低计算所需的时间，1994 年 Agrawal 提出了著名的 Apriori 算法，该算法可以有效减少需要计算的组合的数量，避免组合数量的指数增长，从而在合理的时间内计算出频繁项集。
    Apriori 原理是说：如果一个项集是非频繁集，那么它的所有超集也是非频繁的。
    比如下图中的项集{1，3} 是非频繁集，那么{0，1，3}，{1，2，3}，{0，1，2，3} 就都是非频繁项集。这就大大减少了需要计算的项集的数量。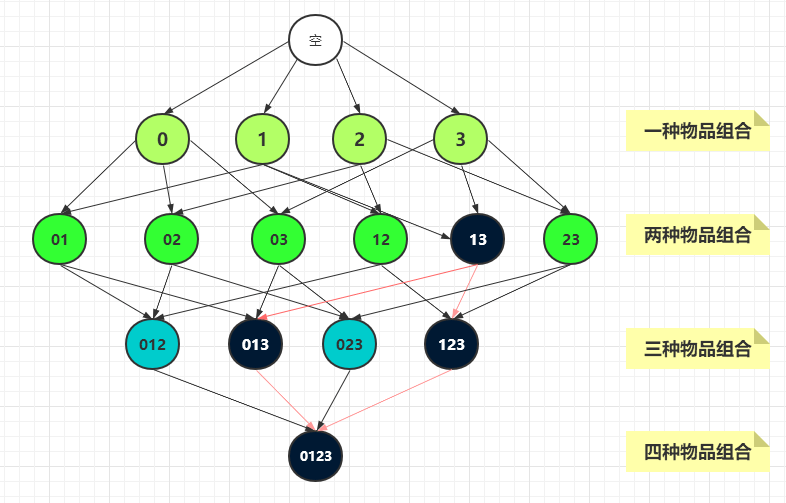
    基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图7

    5，Apriori 算法的实现

    这里，我们使用Apriori 算法来寻找上文表格中的购物清单的频繁项集（为了方便查看，我把表格放在这里）。
交易编号 购物清单
1 牛奶，面包
2 牛奶，面包，火腿
3 面包，火腿，可乐
4 火腿，可乐，方便面
5 面包，火腿，可乐，方便面

efficient_apriori 模块
Efficient-Apriori 包是Apriori 算法的稳定高效的实现，该模块适用于 Python 3.6+。
使用Apriori 算法要先安装：pip install efficient-apriori
efficient_apriori 包中有一个 apriori 函数，原型如下（这里只列出了常用参数）：
apriori(data, min_support = 0.5, min_confidence = 0.5)
参数的含义：

  • data：表示数据集，是一个列表。列表中的元素可以是元组，也可以是列表。
  • min_support：表示最小支持度，小于最小支持度的项集将被舍去。
    • 该参数的取值范围是 [0, 1]，表示一个百分比，比如0.3 表示30%，那么支持度小于30% 的项集将被舍去。
    • 该参数的默认值为0.5，常见的取值有0.5，0.1，0.05。
  • min_confidence：表示最小可信度。
    • 该参数的取值范围也是 [0, 1]。
    • 该参数的默认值为0.5，常见的取值有1.0，0.9，0.8。

使用 apriori 函数
首先，将表格中的购物清单转化成 Python 列表，如下：
data = [
(‘牛奶’, ‘面包’),
(‘牛奶’, ‘面包’, ‘火腿’),
(‘面包’, ‘火腿’, ‘可乐’),
(‘火腿’, ‘可乐’, ‘方便面’),
(‘面包’, ‘火腿’, ‘可乐’, ‘方便面’)
]

挖掘频繁项集和频繁规则：
# 该函数的使用很简单，就一行代码
# 最小支持度为 0.5
# 最小可信度为 1
itemsets, rules = apriori(data, min_support=0.5, min_confidence=1)

查看频繁项集和频繁规则：
>>> itemsets # 频繁项集
{1: { # 只有一个元素的项集
(‘面包’,): 4, # 4 表示记录数
(‘火腿’,): 4,
(‘可乐’,): 3
},
2: { # 有两个元素的项集
(‘火腿’, ‘面包’): 3,
(‘可乐’, ‘火腿’): 3
}
}
>>> rules # 频繁规则
[{可乐} -> {火腿}]

6，总结

本篇文章主要介绍了什么是关联分析，关联分析中三个重要的概念，以及 Apriori 算法。
Apriori 算法用于加快关联分析的速度，但它也需要多次扫描数据集。其实除了Apriori 算法，还有其它算法也可以加快寻找频繁项集的速度。
2000 年提出的FP-Growth 算法，对 Apriori 算法进行了改进。FP-Growth 通过创建一棵 FP树来存储频繁项集。对不满足最小支持度的项不会创建节点，减少了存储空间。而且整个生成过程只遍历数据集 2 次，大大减少了计算量。
另外，还有CBA 算法，GSP 算法等，都对Apriori算法进行了改进，这里不再详细介绍。

【4】Apriori、FP-growth算法一步一步实现

详情看：https://www.cnblogs.com/lsqin/p/9342926.html

1、#Apriori算法实现

  1. #Apriori算法实现
  2. from numpy import *
  4. def loadDataSet():
  5.     return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
  7. # 获取候选1项集，dataSet为事务集。返回一个list，每个元素都是set集合
  8. def createC1(dataSet):
  9.     C1 = []   # 元素个数为1的项集（非频繁项集，因为还没有同最小支持度比较）
  10.     for transaction in dataSet:
  11.         for item in transaction:
  12.             if not [item] in C1:
  13.                 C1.append([item])
  14.     C1.sort()  # 这里排序是为了，生成新的候选集时可以直接认为两个n项候选集前面的部分相同
  15.     # 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在，所以要将候选1项集的每一个元素都转化为一个单独的集合。
  16.     return list(map(frozenset, C1))   #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合（frozenset，Python中的数据结构）
  18. # 找出候选集中的频繁项集
  19. # dataSet为全部数据集，Ck为大小为k（包含k个元素）的候选项集，minSupport为设定的最小支持度
  20. def scanD(dataSet, Ck, minSupport):
  21.     ssCnt = {}   # 记录每个候选项的个数
  22.     for tid in dataSet:
  23.         for can in Ck:
  24.             if can.issubset(tid):
  25.                 ssCnt[can] = ssCnt.get(can, 0) + 1   # 计算每一个项集出现的频率
  26.     numItems = float(len(dataSet))
  27.     retList = []
  28.     supportData = {}
  29.     for key in ssCnt:
  30.         support = ssCnt[key] / numItems
  31.         if support >= minSupport:
  32.             retList.insert(0, key)  #将频繁项集插入返回列表的首部
  33.         supportData[key] = support
  34.     return retList, supportData   #retList为在Ck中找出的频繁项集（支持度大于minSupport的），supportData记录各频繁项集的支持度
  36. # 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。
  37. def aprioriGen(Lk, k):
  38.     retList = []
  39.     lenLk = len(Lk)
  40.     for i in range(lenLk):
  41.         for j in range(i + 1, lenLk):
  42.             # 前k-1项相同时，才将两个集合合并，合并后才能生成k+1项
  43.             L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]   # 取出两个集合的前k-1个元素
  44.             L1.sort(); L2.sort()
  45.             if L1 == L2:
  46.                 retList.append(Lk[i] | Lk[j])
  47.     return retList
  49. # 获取事务集中的所有的频繁项集
  50. # Ck表示项数为k的候选项集，最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集，supK为其支持度，Lk和supK由scanD()函数通过Ck计算而来。
  51. def apriori(dataSet, minSupport=0.5):
  52.     C1 = createC1(dataSet)  # 从事务集中获取候选1项集
  53.     D = list(map(set, dataSet))  # 将事务集的每个元素转化为集合
  54.     L1, supportData = scanD(D, C1, minSupport)  # 获取频繁1项集和对应的支持度
  55.     L = [L1]  # L用来存储所有的频繁项集
  56.     k = 2
  57.     while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集
  58.         Ck = aprioriGen(L[k-2], k)   # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集
  59.         Lk, supK = scanD(D, Ck, minSupport)  # Lk表示项数为k的频繁项集，supK为其支持度
  60.         L.append(Lk);supportData.update(supK)  # 添加新频繁项集和他们的支持度
  61.         k += 1
  62.     return L, supportData
  64. if __name__=='__main__':
  65.     dataSet = loadDataSet()  # 获取事务集。每个元素都是列表
  66.     # C1 = createC1(dataSet)  # 获取候选1项集。每个元素都是集合
  67.     # D = list(map(set, dataSet))  # 转化事务集的形式，每个元素都转化为集合。
  68.     # L1, suppDat = scanD(D, C1, 0.5)
  69.     # print(L1,suppDat)
  71.     L, suppData = apriori(dataSet,minSupport=0.7)
  72.     print(L,suppData)

输出：

[[frozenset({5}), frozenset({2}), frozenset({3})], [frozenset({2, 5})], []] {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({2, 5}): 0.75, frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5}

2、# FP树算法实现

  1. # FP树类
  2. class treeNode:
  3.     def __init__(self, nameValue, numOccur, parentNode):
  4.         self.name = nameValue  #节点元素名称，在构造时初始化为给定值
  5.         self.count = numOccur   # 出现次数，在构造时初始化为给定值
  6.         self.nodeLink = None   # 指向下一个相似节点的指针，默认为None
  7.         self.parent = parentNode   # 指向父节点的指针，在构造时初始化为给定值
  8.         self.children = {}  # 指向子节点的字典，以子节点的元素名称为键，指向子节点的指针为值，初始化为空字典
  10.     # 增加节点的出现次数值
  11.     def inc(self, numOccur):
  12.         self.count += numOccur
  14.     # 输出节点和子节点的FP树结构
  15.     def disp(self, ind=1):
  16.         print(' ' * ind, self.name, ' ', self.count)
  17.         for child in self.children.values():
  18.             child.disp(ind + 1)
  20. # =======================================================构建FP树==================================================
  22. # 对不是第一个出现的节点，更新头指针块。就是添加到相似元素链表的尾部
  23. def updateHeader(nodeToTest, targetNode):
  24.     while (nodeToTest.nodeLink != None):
  25.         nodeToTest = nodeToTest.nodeLink
  26.     nodeToTest.nodeLink = targetNode
  28. # 根据一个排序过滤后的频繁项更新FP树
  29. def updateTree(items, inTree, headerTable, count):
  30.     if items[0] in inTree.children:
  31.         # 有该元素项时计数值+1
  32.         inTree.children[items[0]].inc(count)
  33.     else:
  34.         # 没有这个元素项时创建一个新节点
  35.         inTree.children[items[0]] = treeNode(items[0], count, inTree)
  36.         # 更新头指针表或前一个相似元素项节点的指针指向新节点
  37.         if headerTable[items[0]][1] == None:  # 如果是第一次出现，则在头指针表中增加对该节点的指向
  38.             headerTable[items[0]][1] = inTree.children[items[0]]
  39.         else:
  40.             updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
  42.     if len(items) > 1:
  43.         # 对剩下的元素项迭代调用updateTree函数
  44.         updateTree(items[1::], inTree.children[items[0]], headerTable, count)
  46. # 主程序。创建FP树。dataSet为事务集，为一个字典，键为每个事物，值为该事物出现的次数。minSup为最低支持度
  47. def createTree(dataSet, minSup=1):
  48.     # 第一次遍历数据集，创建头指针表
  49.     headerTable = {}
  50.     for trans in dataSet:
  51.         for item in trans:
  52.             headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
  53.     # 移除不满足最小支持度的元素项
  54.     keys = list(headerTable.keys()) # 因为字典要求在迭代中不能修改，所以转化为列表
  55.     for k in keys:
  56.         if headerTable[k] < minSup:
  57.             del(headerTable[k])
  58.     # 空元素集，返回空
  59.     freqItemSet = set(headerTable.keys())
  60.     if len(freqItemSet) == 0:
  61.         return None, None
  62.     # 增加一个数据项，用于存放指向相似元素项指针
  63.     for k in headerTable:
  64.         headerTable[k] = [headerTable[k], None]  # 每个键的值，第一个为个数，第二个为下一个节点的位置
  65.     retTree = treeNode('Null Set', 1, None) # 根节点
  66.     # 第二次遍历数据集，创建FP树
  67.     for tranSet, count in dataSet.items():
  68.         localD = {} # 记录频繁1项集的全局频率，用于排序
  69.         for item in tranSet:
  70.             if item in freqItemSet:   # 只考虑频繁项
  71.                 localD[item] = headerTable[item][0] # 注意这个[0]，因为之前加过一个数据项
  72.         if len(localD) > 0:
  73.             orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] # 排序
  74.             updateTree(orderedItems, retTree, headerTable, count) # 更新FP树
  75.     return retTree, headerTable
  77. # =================================================查找元素条件模式基===============================================
  79. # 直接修改prefixPath的值，将当前节点leafNode添加到prefixPath的末尾，然后递归添加其父节点。
  80. # prefixPath就是一条从treeNode（包括treeNode）到根节点（不包括根节点）的路径
  81. def ascendTree(leafNode, prefixPath):
  82.     if leafNode.parent != None:
  83.         prefixPath.append(leafNode.name)
  84.         ascendTree(leafNode.parent, prefixPath)
  86. # 为给定元素项生成一个条件模式基（前缀路径）。basePet表示输入的频繁项，treeNode为当前FP树中对应的第一个节点
  87. # 函数返回值即为条件模式基condPats，用一个字典表示，键为前缀路径，值为计数值。
  88. def findPrefixPath(basePat, treeNode):
  89.     condPats = {}  # 存储条件模式基
  90.     while treeNode != None:
  91.         prefixPath = []  # 用于存储前缀路径
  92.         ascendTree(treeNode, prefixPath)  # 生成前缀路径
  93.         if len(prefixPath) > 1:
  94.             condPats[frozenset(prefixPath[1:])] = treeNode.count  # 出现的数量就是当前叶子节点的数量
  95.         treeNode = treeNode.nodeLink  # 遍历下一个相同元素
  96.     return condPats
  98. # =================================================递归查找频繁项集===============================================
  99. # 根据事务集获取FP树和频繁项。
  100. # 遍历频繁项，生成每个频繁项的条件FP树和条件FP树的频繁项
  101. # 这样每个频繁项与他条件FP树的频繁项都构成了频繁项集
  103. # inTree和headerTable是由createTree()函数生成的事务集的FP树。
  104. # minSup表示最小支持度。
  105. # preFix请传入一个空集合（set([])），将在函数中用于保存当前前缀。
  106. # freqItemList请传入一个空列表（[]），将用来储存生成的频繁项集。
  107. def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
  108.     # 对频繁项按出现的数量进行排序进行排序
  109.     sorted_headerTable = sorted(headerTable.items(), key=lambda p: p[1][0])  #返回重新排序的列表。每个元素是一个元组，[（key,[num,treeNode],()）
  110.     bigL = [v[0] for v in sorted_headerTable]  # 获取频繁项
  111.     for basePat in bigL:
  112.         newFreqSet = preFix.copy()  # 新的频繁项集
  113.         newFreqSet.add(basePat)     # 当前前缀添加一个新元素
  114.         freqItemList.append(newFreqSet)  # 所有的频繁项集列表
  115.         condPattBases = findPrefixPath(basePat, headerTable[basePat][1])  # 获取条件模式基。就是basePat元素的所有前缀路径。它像一个新的事务集
  116.         myCondTree, myHead = createTree(condPattBases, minSup)  # 创建条件FP树
  118.         if myHead != None:
  119.             # 用于测试
  120.             print('conditional tree for:', newFreqSet)
  121.             myCondTree.disp()
  122.             mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)  # 递归直到不再有元素
  124. # 生成数据集
  125. def loadSimpDat():
  126.     simpDat = [['r', 'z', 'h', 'j', 'p'],
  127.                ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
  128.                ['z'],
  129.                ['r', 'x', 'n', 'o', 's'],
  130.                ['y', 'r', 'x', 'z', 'q', 't', 'p'],
  131.                ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
  132.     return simpDat
  134. # 将数据集转化为目标格式
  135. def createInitSet(dataSet):
  136.     retDict = {}
  137.     for trans in dataSet:
  138.         retDict[frozenset(trans)] = 1
  139.     return retDict
  141. if __name__=='__main__':
  142.     minSup =3
  143.     simpDat = loadSimpDat()  # 加载数据集
  144.     initSet = createInitSet(simpDat)  # 转化为符合格式的事务集
  145.     myFPtree, myHeaderTab = createTree(initSet, minSup)  # 形成FP树
  146.     # myFPtree.disp()  # 打印树
  148.     freqItems = []  # 用于存储频繁项集
  149.     mineTree(myFPtree, myHeaderTab, minSup, set([]), freqItems)  # 获取频繁项集
  150.     print(freqItems)  # 打印频繁项集

输出：

conditional tree for: {‘s’}
Null Set 1
x 3
conditional tree for: {‘y’}
Null Set 1
z 3
x 3
conditional tree for: {‘x’, ‘y’}
Null Set 1
z 3
conditional tree for: {‘t’}
Null Set 1
x 3
y 2
z 2
z 1
y 1
conditional tree for: {‘t’, ‘y’}
Null Set 1
x 3
conditional tree for: {‘t’, ‘z’}
Null Set 1
x 3
conditional tree for: {‘x’}
Null Set 1
z 3
[{‘r’}, {‘s’}, {‘s’, ‘x’}, {‘y’}, {‘z’, ‘y’}, {‘x’, ‘y’}, {‘z’, ‘x’, ‘y’}, {‘t’}, {‘t’, ‘x’}, {‘t’, ‘y’}, {‘t’, ‘x’, ‘y’}, {‘t’, ‘z’}, {‘t’, ‘z’, ‘x’}, {‘x’}, {‘z’, ‘x’}, {‘z’}]

【5】FP-growth图解案例

https://www.cnblogs.com/datahunter/p/3903413.html

构建FP-tree

FP-growth算法通过构建FP-tree来压缩事务数据库中的信息，从而更加有效地产生频繁项集。FP-tree其实是一棵前缀树，按支持度降序排列，支持度越高的频繁项离根节点越近，从而使得更多的频繁项可以共享前缀。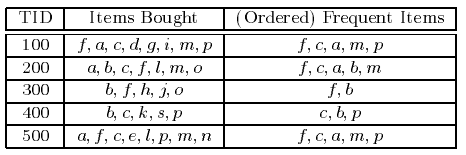
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图8
图2 事务型数据库
图2表示用于购物篮分析的事务型数据库。其中，a，b，…，p分别表示客户购买的物品。首先，对该事务型数据库进行一次扫描，计算每一行记录中各种物品的支持度，然后按照支持度降序排列，仅保留频繁项集，剔除那些低于支持度阈值的项，这里支持度阈值取3，从而得到<(f:4)，(c:4)，(a:3)，(b:3)，(m:3，(p:3)>（由于支持度计算公式中的N是不变的，所以仅需要比较公式中的分子）。图2中的第3列展示了排序后的结果。
FP-tree的根节点为null，不表示任何项。接下来，对事务型数据库进行第二次扫描，从而开始构建FP-tree：
第一条记录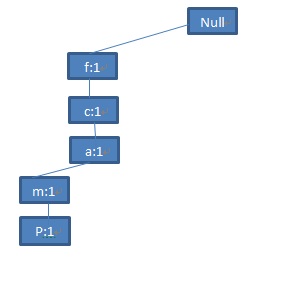对应于FP-tree中的第一条分支<(f:1)，(c:1)，(a:1)，(m:1)，(p:1)>：
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图9
图3 第一条记录
由于第二条记录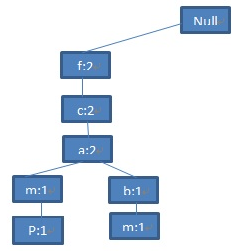与第一条记录有相同的前缀，因此的支持度分别加一，同时在(a:2)节点下添加节点(b:1)，(m:1)。所以，FP-tree中的第二条分支是<(f:2)，(c:2)，(a:2)，(h:1)，(m:1)>：
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图10
图4 第二条记录
第三条记录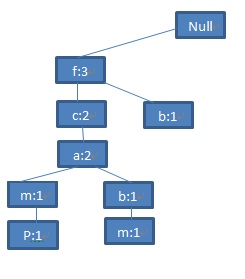与前两条记录相比，只有一个共同前缀，因此，只需要在(f:3)下添加节点：
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图11
图5 第三条记录
第四条记录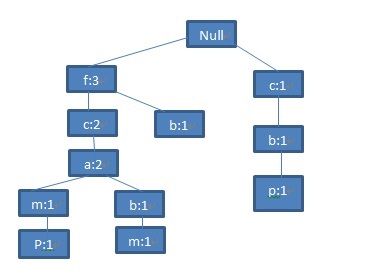与之前所有记录都没有共同前缀，因此在根节点下添加节点(c:1)，(b:1)，(p:1)：
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图12
图6 第四条记录
类似地，将第五条记录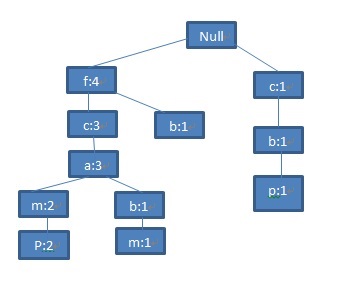作为FP-tree的一个分支，更新相关节点的支持度：
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图13
图7 第五条记录
为了便于对整棵树进行遍历，建立一张项的头表（an item header table）。这张表的第一列是按照降序排列的频繁项。第二列是指向该频繁项在FP-tree中节点位置的指针。FP-tree中每一个节点还有一个指针，用于指向相同名称的节点：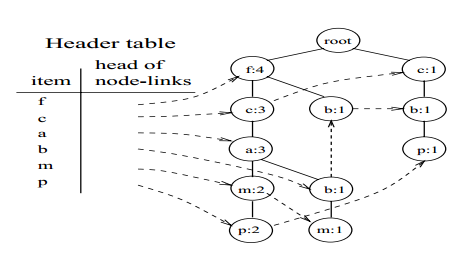
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图14
图8 FP-tree

在韩家炜教授提出FP-growth算法之前，关联分析普遍采用Apriori及其变形算法。但是，Apriori及其变形算法需要多次扫描数据库，并需要生成指数级的候选项集，性能并不理想。FP-growth算法提出利用了高效的数据结构FP-tree，不再需要多次扫描数据库，同时也不再需要生成大量的候选项。

【6】频繁模式挖掘中Apriori、FP-Growth和Eclat算法的实现和对比

https://www.cnblogs.com/infaraway/p/6774521.html

【7】基于SynchroTrap+LPA算法的团伙账户挖掘

https://mp.weixin.qq.com/s?__biz=MzA4OTAwMjY2Nw==&mid=2650189651&idx=1&sn=4d152af90a40a3d78ad5277c3060e1ff&chksm=88238897bf540181716606d8c7dbda8ff51c3a6d580e89dd3c7e1e31cfd2bb60a1647e357b7a&scene=21#wechat_redirect

目标

本文目的：把经常一起行动的人找出来，并划分成一个Group，仅利用时间关系，无需其他介质
上一期的文章，没有解决相隔时间近但是不在同一个5min切片内的的问题，为了解决这个问题，我研究了一些关于时序的关联规则算法，包括GSP、Prefixspan、FreeSpan等，在我们这个场景里面，不能很好的解决。我们用SynchroTrap+LPA这两个，就能非常完美的解决，SynchroTrap算法用来构图，LPA用来分群。有人说，没有介质会不会不准，其实大家可以想象下，在食堂吃饭的时候，有没有连续几天都是同一个你不认识的人排在你的前面？
SynchroTrap+LPA比关联规则算发现较大规模的群体，本文中，我们仅仅利用校园卡消费明细数据和这两个算法，比如班级、室友等，也能发现情侣、基友、闺蜜、渣男、渣女等非常有意思的模式我们一步步来看看怎么做的。

结论：通过上面的案例，我们可以看到SynchroTrap+LPA算法，对于无介质的欺诈用户进行关联和分群，是非常完美的一个组合

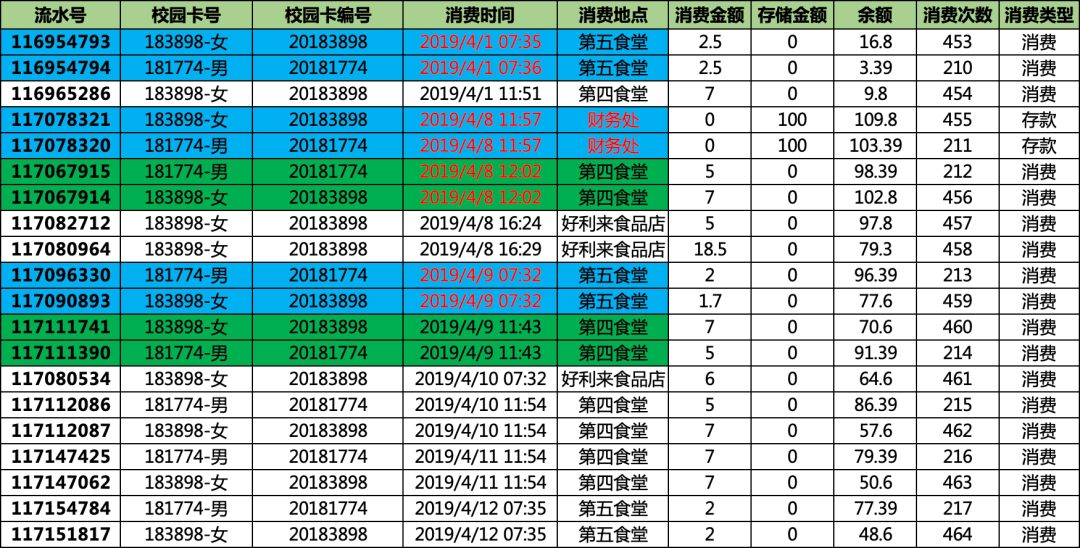
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图15

绘图

https://app.flourish.studio 这个网站绘图
在看看下面，是两个人所有的在5分钟之内的链接，非常紧密和频繁，一看就是很恩爱的情侣。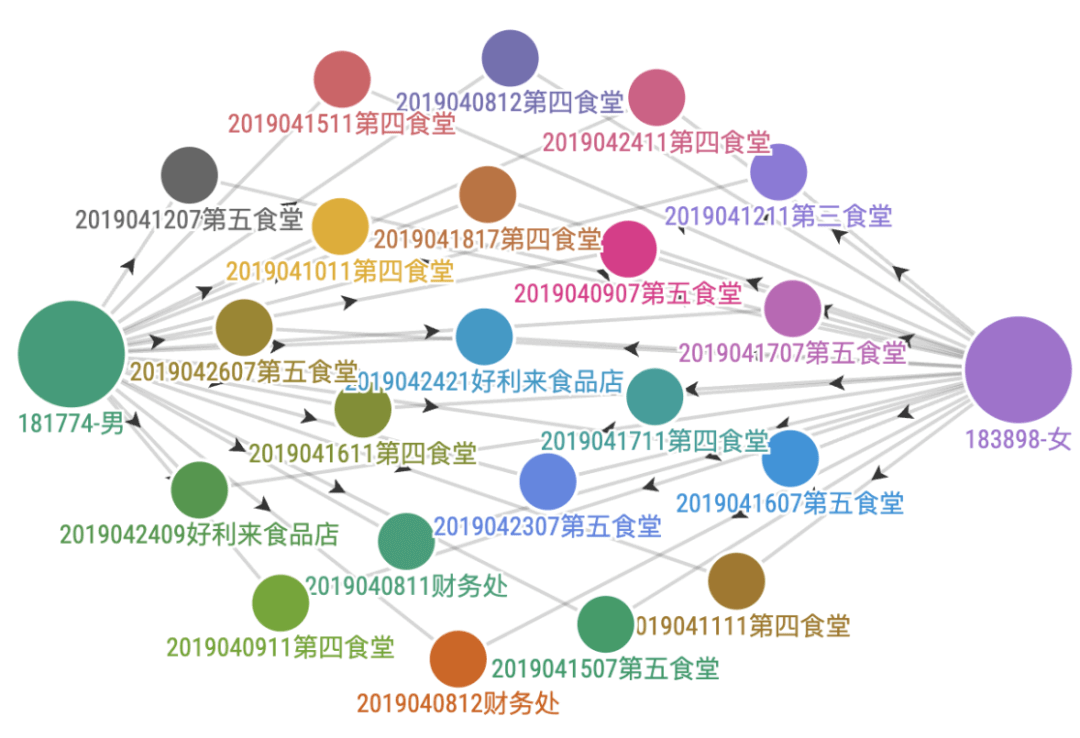
基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图16

用matplotlib.pyplot绘图试试，简直没法看

基于时空关联挖掘 %26 关联分析Apriori\FP-growth算法介绍 %26 基于SynchroTrap+LPA算法的团伙账户挖掘 - 图17

SynchroTrap+LPA算法的挖掘代码

  1. # -*- coding: utf-8 -*-
  4. # 数据读取
  5. import numpy as np
  6. import pandas as pd
  7. import os
  9. pd.set_option('display.max_columns', None)
  10. os.chdir("/Users\yingtao.xiang\Downloads\Analysis-of-students-consumption-behavior-on-campus-master\Analysis-of-students-consumption-behavior-on-campus-master\data")
  11. data1 = pd.read_csv("data1.csv", encoding="gbk")
  12. data2 = pd.read_csv("data2.csv", encoding="gbk")
  13. data3 = pd.read_csv("data3.csv", encoding="gbk")
  15. data1.columns = ['序号', '校园卡号', '性别', '专业名称', '门禁卡号']
  16. data2.columns = ['流水号', '校园卡号', '校园卡编号', '消费时间', '消费金额', '存储金额', '余额', '消费次数', '消费类型', '消费项目编码', '消费项目序列号', '消费操作编码', '操作编码', '消费地点']
  17. data3.columns = ['序号', '门禁卡号', '进出时间', '进出地点', '是否通过', '描述']
  19. print(data1.head(3))
  20. # 序号    校园卡号 性别    专业名称      门禁卡号
  21. # 0   1  180001  男  18国际金融  19762330
  22. # 1   2  180002  男  18国际金融  20521594
  23. # 2   3  180003  男  18国际金融  20513946
  25. print(data2.head(3))
  26. # 流水号      校园卡号     校园卡编号             消费时间  消费金额  存储金额     余额  消费次数  \
  27. # 0  117342773  181316-女  20181316  2019/4/20 20:17   3.0   0.0  186.1   818   
  28. # 1  117344766  181316-女  20181316   2019/4/20 8:47   0.5   0.0  199.5   814   
  29. # 2  117346258  181316-女  20181316   2019/4/22 7:27   0.5   0.0  183.1   820   
  31. #   消费类型  消费项目编码 消费项目序列号  消费操作编码  操作编码  消费地点 性别  
  32. # 0   消费      49     NaN     NaN   235  第一食堂  女  
  33. # 1   消费      63     NaN     NaN    27  第二食堂  女  
  34. # 2   消费      63     NaN     NaN    27  第二食堂  女  
  36. print(data3.head(3))
  37. #  序号      门禁卡号           进出时间       进出地点  是否通过    描述
  38. # 0  1330906  25558880  2019/4/1 0:00  第六教学楼[进门]     1  允许通过
  39. # 1  1330907  18413143  2019/4/1 0:02  第六教学楼[出门]     1  允许通过
  40. # 2  1331384  11642752  2019/4/1 0:00    飞凤轩[进门]     1  允许通过
  43. # 数据处理~~~~~~~~~~~~~~~~~
  45. data2 = data2.merge(data1[['校园卡号','性别']],on='校园卡号')
  47. data2['校园卡号'] = data2['校园卡号'].apply(lambda x: str(x))+'-'+data2['性别'] # 校园卡号处理，加上性别
  49. # 时间格式调整,转换成比较标准的格式，方便后面的处理
  50. import datetime
  51. def st_pt(x):
  52.     #'2019/4/20 20:17'=>'2019-04-20 20:17:00'
  53.      return str(datetime.datetime.strptime(x, "%Y/%m/%d %H:%M"))
  55. # 时间离散化，每个五分钟一个类型
  56. def time_5(s):
  57.     #'2022-02-22 17:46:07'=>'2022-02-22 17_9'
  58.     a = str(round(int(s.split(':')[1])/5))
  59.     return s.split(':')[0]+'_'+a
  61. # 数据处理，处理成标准的格式
  62. df = data2
  63. df = df.sort_values(by='消费时间',ascending=True) 
  64. df['消费时间_F'] = df['消费时间'].apply(st_pt)  # 转换为标准时间
  65. df['消费时间_5'] = df['消费时间_F'].apply(time_5) # 每5分钟一个间隔，一个小时12个
  68. print(df.head(3))
  69. #              流水号      校园卡号     校园卡编号            消费时间  消费金额  存储金额     余额  消费次数  \
  70. # 57869  116925030  180641-女   2018641  2019/4/1 10:00   3.5   0.0  206.7   804   
  71. # 60120  116969953  181021-女  20181021  2019/4/1 10:00   2.0   0.0  127.9   512   
  72. # 63191  116969952  181036-女  20181036  2019/4/1 10:00   3.0   0.0   12.6   451   
  74. #       消费类型  消费项目编码 消费项目序列号  消费操作编码  操作编码   消费地点 性别               消费时间_F  \
  75. # 57869   消费     107     NaN     NaN   135  红太阳超市  女  2019-04-01 10:00:00   
  76. # 60120   消费      12     NaN     NaN   236   第一食堂  女  2019-04-01 10:00:00   
  77. # 63191   消费      12     NaN     NaN   236   第一食堂  女  2019-04-01 10:00:00   
  79. #                 消费时间_5  
  80. # 57869  2019-04-01 10_0  
  81. # 60120  2019-04-01 10_0  
  82. # 63191  2019-04-01 10_0  
  84. print(df['消费时间_5'].unique())
  85. print(pd.DataFrame(df['消费时间_5'].unique()).value_counts()) #打印出来 6176个唯一值
  87. all_list = []
  88. for v in df['消费时间_5'].unique():
  89.     one = df[df['消费时间_5']==v]['校园卡号'].unique().tolist()
  90.     all_list.append(one)
  93. # df[df['消费时间_5']==v]['校园卡号']
  94. # Out[47]: 
  95. # 211747    180104-女
  96. # 106417    180694-女
  97. # 106418    180694-女
  98. # 182463    180008-男
  99. # 3697      180826-女
  100. # 15368     182748-男
  101. # 76287     181202-女
  102. # 10412     181891-男
  103. # Name: 校园卡号, dtype: object
  105. # one
  106. # Out[49]: 
  107. # ['180104-女',
  108. #  '180694-女',
  109. #  '180008-男',
  110. #  '180826-女',
  111. #  '182748-男',
  112. #  '181202-女',
  113. #  '181891-男']
  116. print(len(all_list))#可以看到，有6176个时间片段，可以类比6176个订单
  117. # 6176
  119. all_list # 看看list长什么样子    
  120. # [['181735-女','180015-女'],['181058-男', '181374-男', '182044-女', '182581-女', '180052-女', '182729-男'],['181405-男','180078-男'],···]
  123. #数据保存起来
  124. df.to_csv('df.csv',header=True,index=False)
  127. # 关联规则挖掘~~~~~~~~~~~~~~
  129. #加载包，没有的自行安装
  130. #pip install efficient-apriori
  132. from efficient_apriori import apriori
  134. # Apriori 算法是一种发掘事物内在关联关系的算法，它可以加快关联分析的速度，从而让我们更有效的进行关联分析。
  136. # 关联分析 
  137. # 来源：https://www.cnblogs.com/codeshell/p/14113600.html
  138. # 关联分析用于发掘大规模数据集中的内在关系。
  139. # 关联分析一般要分析数据集中的频繁项集（frequent item sets）和关联规则（association rules）：
  140. # 频繁项集：是数据集中频繁项的集合，集合中可以有一项或多项物品。
  141. # 关联规则：暗示了两种物品之间可能存在很强的内在关系。
  143. itemsets, rules = apriori(all_list, min_support=0.005,  min_confidence=1)
  145. itemsets[2]
  146.  # ('183305-女', '183317-女'): 38,
  147.  # ('183308-女', '183317-女'): 42,
  148.  # ('183310-女', '183314-女'): 31,
  149.  # ('183315-女', '183324-女'): 32,
  150.  # ('183338-男', '183345-男'): 40,
  151.  # ('183343-男', '183980-女'): 44,
  152.  # ('183385-女', '183401-女'): 40,
  153.  # ('183386-女', '183409-女'): 34,
  154.  # ('183408-女', '183415-女'): 42,
  155.  # ('183414-女', '183418-女'): 41,
  156.  # ('183419-女', '183420-女'): 56,
  157.  # ('183419-女', '183422-女'): 59,
  158.  # ···
  159. len(itemsets[2]) # 一共有三百多对，我们下面挑一部分来分析
  160. # 378
  163. # 基于SynchroTrap+LPA算法的团伙账户挖掘~~~~~~~~~~~~~~~~~~~~~~~~~~~
  164. # 1、读取数据
  165. data1 = pd.read_csv("data1.csv", encoding="gbk")
  166. data2 = pd.read_csv("data2.csv", encoding="gbk")
  167. data3 = pd.read_csv("data3.csv", encoding="gbk")
  168. data1.columns = ['序号', '校园卡号', '性别', '专业名称', '门禁卡号']
  169. data2.columns = ['流水号', '校园卡号', '校园卡编号', '消费时间', '消费金额', '存储金额', '余额', '消费次数', '消费类型', '消费项目编码', '消费项目序列号', '消费操作编码', '操作编码', '消费地点']
  170. data3.columns = ['序号', '门禁卡号', '进出时间', '进出地点', '是否通过', '描述']
  171. print(data1.head(3))
  172. print(data2.head(3))
  173. print(data3.head(3))
  175. # 数据匹配，匹配上性别数据，分析更直观
  176. data2 = data2.merge(data1[['校园卡号','性别']],on='校园卡号')
  177. data2['校园卡号'] = data2['校园卡号'].apply(lambda x: str(x))+'-'+data2['性别']
  180. # 2、时间切片处理
  181. import datetime
  182. '''
  183. 函数功能
  184. 时间格式调整
  185. '2019/4/20 20:17'=>'2019-04-20 20:17:00'
  186. '''
  187. def st_pt(x):
  188.      return str(datetime.datetime.strptime(x, "%Y/%m/%d %H:%M"))
  189. '''
  190. 函数功能
  191. 时间切片
  192. 5分钟一个切片，且每个时间会切成两个片段
  193. Time2Str('2021-11-16 15:51:39' )
  194. '2021-11-16 15:51:39'  => '2021111615(10);2021111615(11)'
  195. '''
  196. def Time2Str(tsm):
  197.     t0 = datetime.datetime.fromisoformat(tsm)
  198.     t1 = t0+datetime.timedelta(days=0, hours=5/60)
  199.     str1 = t0.strftime("%Y%m%d%H")+'(' +str(round(int(t0.minute/5))).rjust(2,'0')+')'
  200.     str2 = t1.strftime("%Y%m%d%H")+'(' +str(round(int(t1.minute/5))).rjust(2,'0')+')'
  201.     return str1+';'+str2
  203. # 开始数据处理
  204. df = data2
  205. df['消费时间'] = df['消费时间'].apply(st_pt)
  206. df['tsm']     = df['消费时间'].apply(Time2Str)
  208. # 数据分裂，一行变两行
  209. df = df.set_index(["校园卡号", "消费时间",'消费地点'])["tsm"].str.split(";", expand=True)\
  210.     .stack().reset_index(drop=True, level=-1).reset_index().rename(columns={0: "tsm"})
  211. print(df)
  212. # # 可以看到，处理后的格式如下
  213. #     校园卡号                 消费时间    消费地点             tsm
  214. # 0       180641-女  2019-04-01 10:00:00   红太阳超市  2019040110(00)
  215. # 1       180641-女  2019-04-01 10:00:00   红太阳超市  2019040110(01)
  216. # 2       181021-女  2019-04-01 10:00:00    第一食堂  2019040110(00)
  217. # 3       181021-女  2019-04-01 10:00:00    第一食堂  2019040110(01)
  218. # 4       181036-女  2019-04-01 10:00:00    第一食堂  2019040110(00)
  220. # 3、匹配构图
  222. # 数据匹配，加入时间约束和地点约束
  223. df_0 = pd.merge(df,df,on =['tsm','消费地点'],how='inner')
  224. df_0.shape
  226. # 排除 自己和自己匹配的数据
  227. df_1 = df_0[df_0['校园卡号_x']!=df_0['校园卡号_y']]
  229. # 时间作差，大于5分钟的排除
  230. df_1['diff'] = (pd.to_datetime(df_1['消费时间_x'])-pd.to_datetime(df_1['消费时间_y'])).dt.seconds/60
  231. df_1 = df_1[df_1['diff']<=5]
  233. # 提取小时 按共同出现的小时计数
  234. df_1['date'] = df_1['tsm'].apply(lambda x :x[0:10])
  236. #统计两两关联的次数，这里比较简单，不按天，也不计算相似度了
  237. df_2 = df_1.groupby(['校园卡号_x','校园卡号_y']).agg({'date': pd.Series.nunique}).reset_index()
  239. # 降序排列
  240. df_2 = df_2.sort_values(by='date',ascending=False) 
  242. #  校园卡号_x    校园卡号_y  date
  243. # 1031801  181293-女  181268-女    68
  244. # 1008844  181268-女  181293-女    64
  245. # 343421   180399-女  183665-女    60
  246. # 309673   180363-女  181876-女    58
  247. # 1967448  182392-女  182377-女    58
  248. #           ...       ...   ...
  249. # 1509502  181840-男  181732-女     1
  250. # 1509501  181840-男  181731-女     1
  251. # 1509499  181840-男  181729-女     1
  252. # 1509497  181840-男  181727-女     1
  253. # 1645283  181999-男  183585-女     1
  255. df_2.shape
  256. # (3290566, 3)
  258. # 4、阈值确定
  259. # 图数据好了，但是我们看有300多万，很多一个月就一次，这个肯定就是巧合数据，每次你去食堂排队，排队前后的，
  260. # 和你的时间间隔就比较少，但是偶尔的关联，并不是我们想要的，所以我们要进一步筛选这里我确定20次，数据瞬间从300万到1924了。
  263. # 给关系加阈值，大于20次的算是比较强的关联了
  264. df_3 = df_2[df_2['date']>=20]
  266. df_3.shape
  267. # (1924, 3)
  269. df_3
  270. #  校园卡号_x    校园卡号_y  date
  271. # 1031801  181293-女  181268-女    68
  272. # 1008844  181268-女  181293-女    64
  273. # 343421   180399-女  183665-女    60
  274. # 309673   180363-女  181876-女    58
  275. # 1967448  182392-女  182377-女    58
  276. #           ...       ...   ...
  277. # 156386   180173-女  180109-女    20
  278. # 271647   180320-女  183546-女    20
  279. # 2884196  183692-女  180377-女    20
  280. # 66844    180085-女  180394-女    20
  281. # 1801477  182194-女  182212-女    20
  283. # 5、LPA分群
  284. import matplotlib.pyplot as plt
  285. import networkx as nx
  286. from networkx.algorithms.community import asyn_lpa_communities as lpa
  289. df_4 = df_2[df_2['date']>=45] # 把阈值提高点
  291. # 数据格式转换
  292. # tuples = [tuple(x) for x in df_3[['校园卡号_x','校园卡号_y']].values]
  293. tuples = [tuple(x) for x in df_4[['校园卡号_x','校园卡号_y']].values]
  295. G = nx.DiGraph()
  296. G.add_edges_from(tuples)
  298. # LPA本身不稳定，因此，社群存在小范围波动
  299. com = list(lpa(G))  #如果样本过多，可能运行很久不出来 
  301. # NetworkXError: random_state_index is incorrect
  303. # 原因：
  304. # 其实是decorator版本问题，报错电脑上的decorator的版本是5.0，而没有报错的版本为4.4.2，注意，我的networkx版本为2.5.
  306. # 解决办法：
  307. # 将decorator版本降为4.4.2  pip install decorator==4.4.2
  310. # 或者解决方法：
  311. # 第一：打开Anaconda Prompt(Anaconda3),将networkx包和decorator包降级，输入如下code：
  313. # pip install --user decorator==4.3.0
  314. # pip install --user networkx==2.3
  316. # 然后重新打开！
  318. print('社区数量',len(com))
  319. # 449
  321. # 打印分群数据 仅展示部分数据
  322. for i in com:
  323.     print(i)
  324. # {'181559-男', '181568-男', '181556-男', '181564-男'}
  325. # {'181013-女', '181042-女', '180624-男'}
  326. # {'180851-女', '181461-男', '180780-女', '180856-女'}
  327. # {'180105-女', '180164-女', '180198-女', '180118-女'}
  328. # {'183401-女', '183385-女'}
  329. # {'181364-男', '181528-男'}
  330. # {'182031-男', '182029-男', '182016-男', '182033-男'}
  331. # {'182039-男', '182042-男', '182041-男', '182040-男'}
  332. # {'183706-女', '183691-女'}
  333. # {'180449-女', '180491-女', '180489-女', '180455-女', '180456-女', '180476-女'}
  334. # {'181013-女', '181042-女', '180624-男'}
  335. # {'182283-女', '182244-女'}  
  336. # {'181623-男', '183847-女', '181597-男'}
  338. # 6、明细数据获取
  339. # 为了进行比较明细的分析，我们可以挑一些我们比较感兴趣的关系对，进行明细数据分析
  341. # 渣女组合
  342. result = data2[(data2['校园卡号']=='181623-男') | (data2['校园卡号']=='183847-女') | \
  343.       (data2['校园卡号']=='181597-男')]
  344. # 情侣组合
  345. result = data2[(data2['校园卡号']=='181774-男') | (data2['校园卡号']=='183898-女')]
  346. result = result.sort_values(by='消费时间')
  348. # 用户 -时间-地点关系数据
  349. result = df_1[((df_1['校园卡号_x']=='181774-男') & (df_1['校园卡号_y']=='183898-女')) | \
  350.               ((df_1['校园卡号_y']=='181774-男') & (df_1['校园卡号_x']=='183898-女'))]
  352. # 数据整理保存备用
  353. result.to_csv('resualt.csv',index=False,header=True)
  356. # 7、数据可视化
  357. # 我们再看一个渣男渣女组合，大家可以自己去看看呢，上面的绘图，可以使用https://app.flourish.studio这个网站。
  359. # 用matplotlib.pyplot绘图试试，简直没法看
  361. # 下面是画图 
  362. pos = nx.spring_layout(G) # 节点的布局为spring型
  363. NodeId    = list(G.nodes())
  364. node_size = [G.degree(i)**1.2*90 for i in NodeId] # 节点大小
  366. plt.figure(figsize = (8,6)) # 图片大小
  367. nx.draw(G,pos, with_labels=True, 
  368.         node_size =node_size, 
  369.         node_color='w', 
  370.         node_shape = '.'
  371.         )
  372. # AttributeError: module 'matplotlib.cbook' has no attribute 'iterable'
  374. # pip install matplotlib==3.1.0 可能版本过高，重新安装
  376. '''
  377. node_size表示节点大小
  378. node_color表示节点颜色
  379. with_labels=True表示节点是否带标签
  380. '''
  382. # color_list = ['pink','orange','r','g','b','y','m','gray','black','c','brown']
  384. color_list = ['pink','orange','r','g','b','y','m','gray','black','c','brown'
  385.               ,'pink','orange','r','g','b','y','m','gray','black','c','brown'
  386.               ,'pink','orange','r','g','b','y','m','gray','black','c','brown'
  387.               ,'pink','orange','r','g','b','y','m','gray','black','c','brown']
  389. # for i in range(len(com)):
  390. # len(com)
  391. # Out[21]: 19
  393. for i in range(len(com)):
  394.     nx.draw_networkx_nodes(G, pos, nodelist = com[i], 
  395.                            node_color=color_list[i+2],  
  396.                            label=True)
  398.     # IndexError: list index out of range   color_list[i+2] 这里
  402. # 重新尝试下
  403. for i in range(len(com)):
  404.     nx.draw_networkx_nodes(G, pos, nodelist = com[i], 
  405.                            label=True)
  407. plt.show()