OR(Odds ratio)-比值比、优势比
OR(Odds ratio)比值比,也称优势比,指病例组中暴露人数与非暴露人数的比值除以对照组中暴露人数与非暴露人数的比值。反映的是疾病和暴露的关联强度,通常出现在病例-对照研究里。举个具体的例子,研究心梗的病因时选择100名心梗患者做为病例,以100名没有发生过心梗的患者作为对照,比较他们发生心梗的可能病因。假设在发生心梗的人群中,患高血压是40人,而在没发生过心梗的人群中患高血压20人。那么我们可以得到以下的四格表: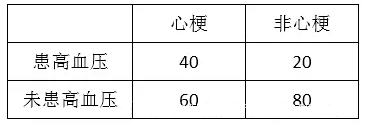
那么OR=(40/60)/(20/80)=4080/2060=2.67。那么这2.67说明什么呢?其意义基本上可以等同为:患高血压的人发生心梗的风险是未患高血压的人的2.67倍。
那论文里常常出现的危险因素、保护因素是什么意思呢?研究人员在进行统计得到OR值的时候,会把OR值和1进行比较,如果某个因素OR值大于1,那么这个因素就是患病的危险因素;也就是携带这个因素的人,患病的风险高。如果OR值小于1,那么这个因素就是患病的保护因素;有这个因素的人患病的风险低。
为什么我们能做出这样的判断呢?我们先来假设一下,假如患高血压和发生心梗无关,那么可以推论,患高血压的人和不患高血压的人心梗的发生率是一样的。也就是说,患高血压的人的心梗发生率=未患高血压的人。因为病例对照研究得不到发病率,所以我们只好推论改成:心梗病例中高血压/无高血压的比值和非心梗对照中高血压/无高血压的比值相同。在上面这个假设成立的时候,我们得到的OR值是多少呢?OR=(心梗病例中高血压/无高血压的比值)/( 非心梗对照中高血压/无高血压的比值)=1。通过上面这样一说大家应该明白为啥我们的OR值都要和1比了吧。
OR值在回归模型中的解读
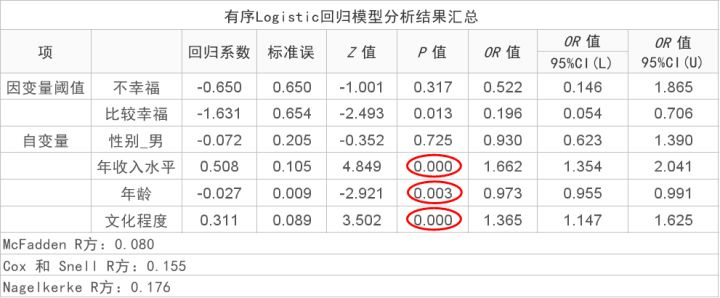
表4 有序Logistic回归模型分析结果汇总
表4是模型结果分析汇总表,用于展示模型的结果,可以说是最为重要的结果,包括回归系数的显著性,模型R方值等。
上表格中包括因变量阈值,其值基本无意义,仅从数学角度上看有此值输出而已。同时输出Cox and Snell,Nagelkerke和McFadden,三种常用的计算伪决定系数的方法,通常伪决定系数不会太高,不需要过多关注。
从上表可知:模型伪R平方值(McFadden R平方)为0.080,意味着性别, 年龄, 学历, 年收入水平可以解释幸福水平的8.0%变化原因。
具体分析,年收入水平,回归系数值为0.508,并且呈现出0.01水平的显著性(z=4.849,P=0.000<0.01),意味着年收入水平会对幸福水平产生显著的正向影响关系。**OR值为1.662,说明年收入水平增加一个单位时,幸福水平的变化(增加)幅度为1.662倍。**
年龄、文化程度同年收入水平均对幸福水平产生显著性影响,这里不再展开分析。
总结分析可知:学历, 年收入水平会对幸福水平产生显著的正向影响关系,以及年龄会对幸福水平产生显著的负向影响关系。
OR 值如何计算
Excel函数计算
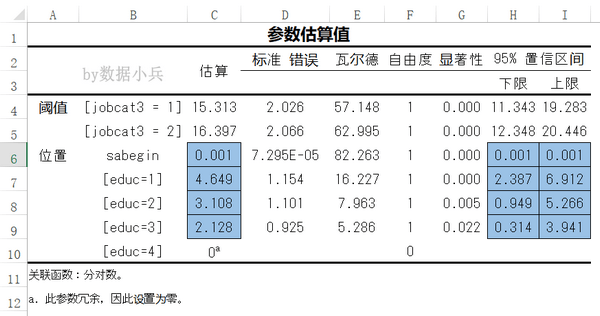
将SPSS参数估计表复制到Excel表中,针对回归系数B列及其95%置信区间共三列数据,用EXP()函数计算OR值及置信区间。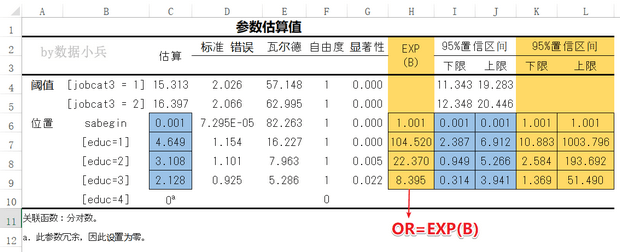
本例,插入H列,在H6单元格输入公式 EXP(C6),并向下填充值H9,即可快速计算各回归系数对应的OR值,同理将参数换成回归系数的95%置信区间上下限,也可以计算OR值的95%置信区间。
第二种
广义线性模型
通过广义线性模型菜单模块也可以执行有序logistic回归分析,在这个模块下SPSS可以计算参数的OR值输出相应的结果。注意此模块不能输出平行检验。
【分析】→【广义线性模型】,【模型类型】下勾选【有序logistic】。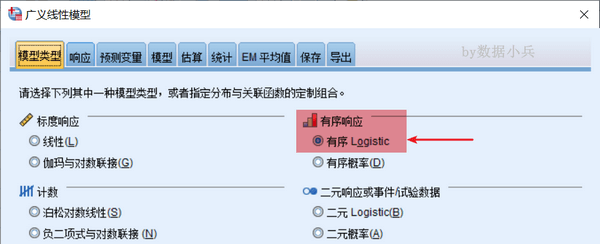
依次在【响应】、【预测变量】下设定好因变量和自变量,【模型】下选择考虑主效应即可。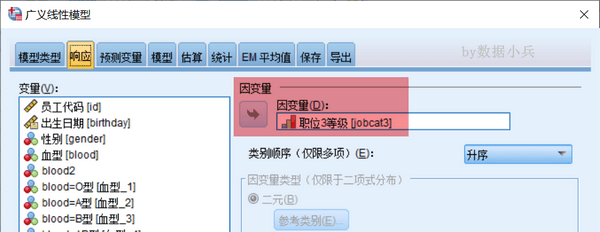
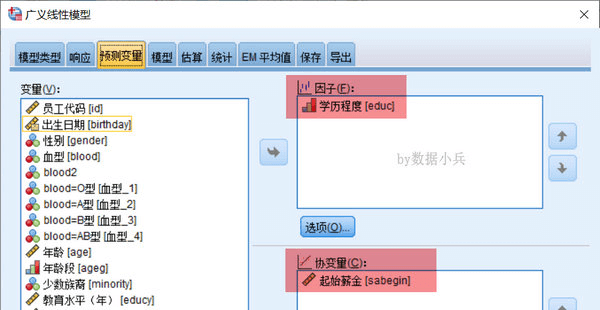
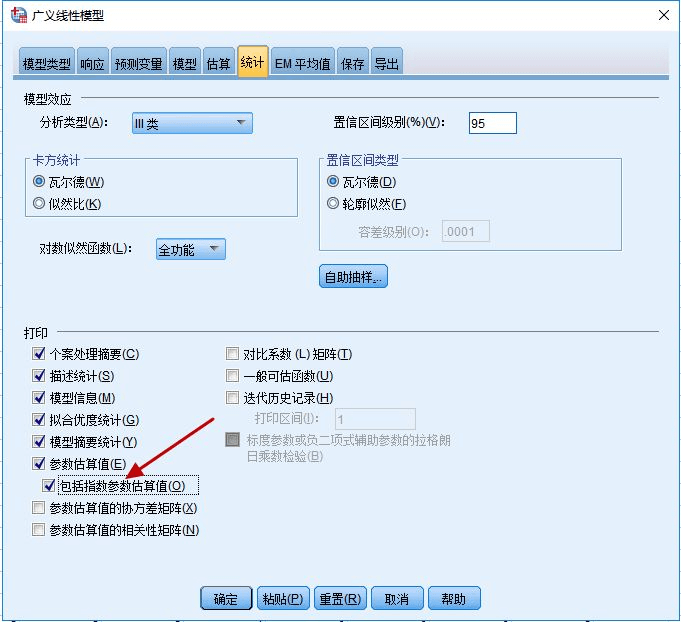
【统计】下勾选【包括指数参数估算值】。其他默认,执行分析。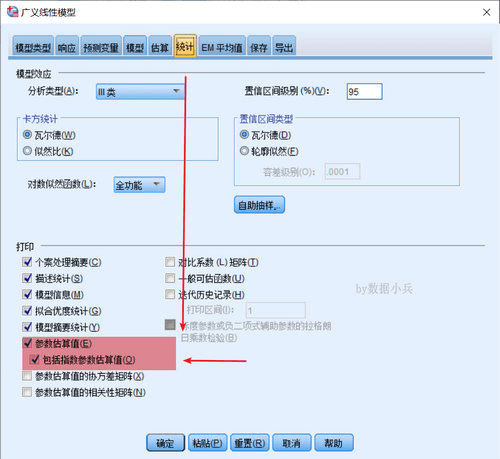
来看结果,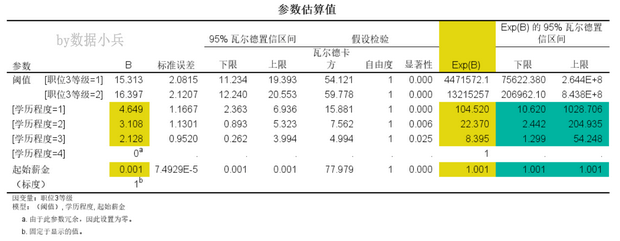
OR值和Excel计算的基本一致。
SPSS操作
https://blog.csdn.net/weixin_42398056/article/details/112571547
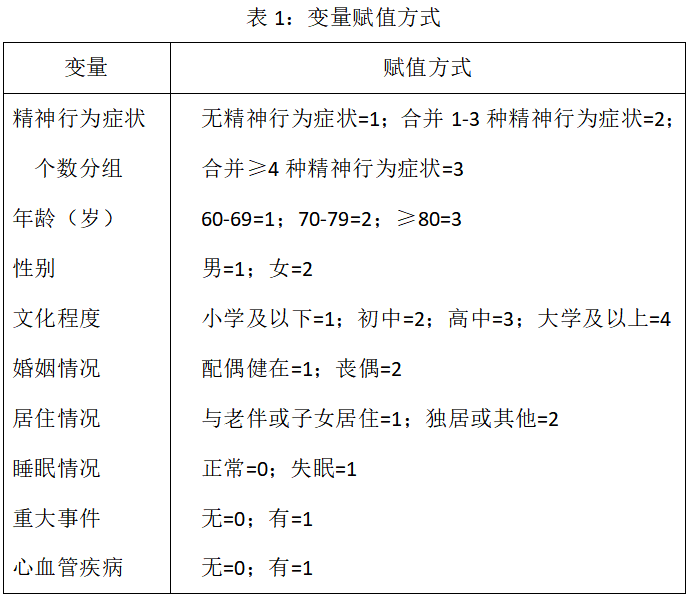
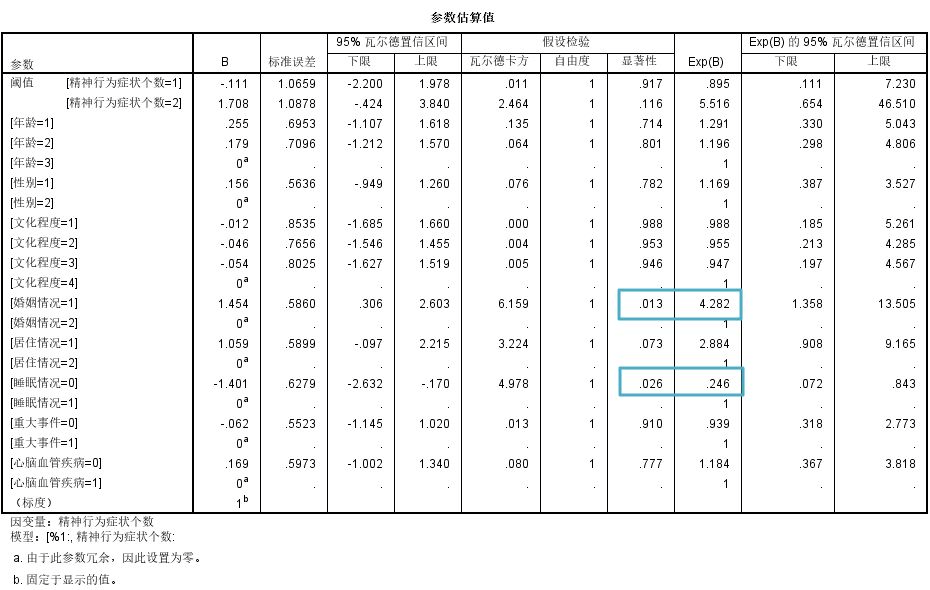
由结果可以看出:配偶健在的MCI老年人精神行为症状的发生率是丧 偶MCI老年人的4.282倍(OR=4.282,P=0.013);睡眠正常MCI老年人精神行为症状的发生率是存在失眠情况的0.246倍(OR=0.246,P=0.026),即存在失眠情况的MCI老年人精神行为症状的发生率是睡眠正常的4.07倍。
[
](https://blog.csdn.net/weixin_42398056/article/details/112571547)