评分卡模型如何快速搭建?——本文旨在从0-1完成基础的评分卡模型,另附完全代码见文末.
步骤一栏:
1.准备样本(划分三个样本:训练集(dev)、验证集(val)、跨时间集(off))
2.清洗数据(缺失、异常、数据类型转换等)
3.特征挖掘(分箱IV计算、psi计算、变量组合、剔除无价值变量)
4.生成二分类模型(LR、Xgboost、Gbdt等)
5.计算各模型在各样本的表现(计算F、ROC、KS、PSI值,挑选合适模型)
6.生成模型报告并制作评分卡(根据模型得到的特征权重计算出具体变量的分值)
1、准备数据
选样本,结合实际情况选取合适的样本,另外将样本分成3份:训练集、验证集、跨时间集(用于验证模型稳定性)
本案例样本如下:
scorecard.txt
详细:[95806 rows x 13 columns] 最后一列指样本类型:训练集(dev)、验证集(val)、跨时间集(off)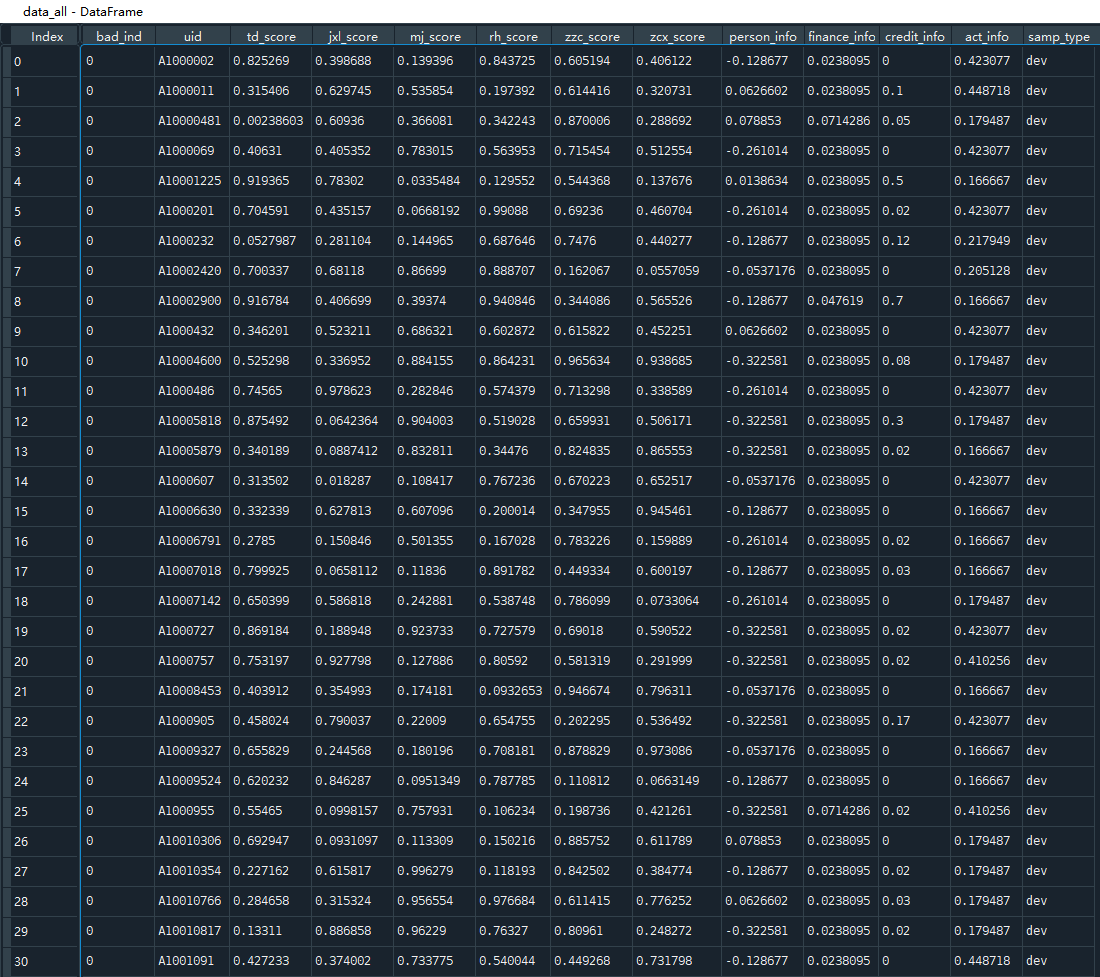
划分开发样本、验证样本与跨时间(时间外)样本
训练集(dev)、验证集(val)、跨时间集(off)>>7:1.5:1.5>> 65304:14527:15975
dev = data_all[(data_all[‘samp_type’] == ‘dev’)] # 65304
val = data_all[(data_all[‘samp_type’] == ‘val’)] # 14527
off = data_all[(data_all[‘samp_type’] == ‘off’)] # 15975
2、清洗数据
因样本较好,无异常数据,这步跳过
代码:toad.detector.detect(data_all) # 观测数据的缺失情况、具体的值类别、均值、标准差、分位数、最大最小等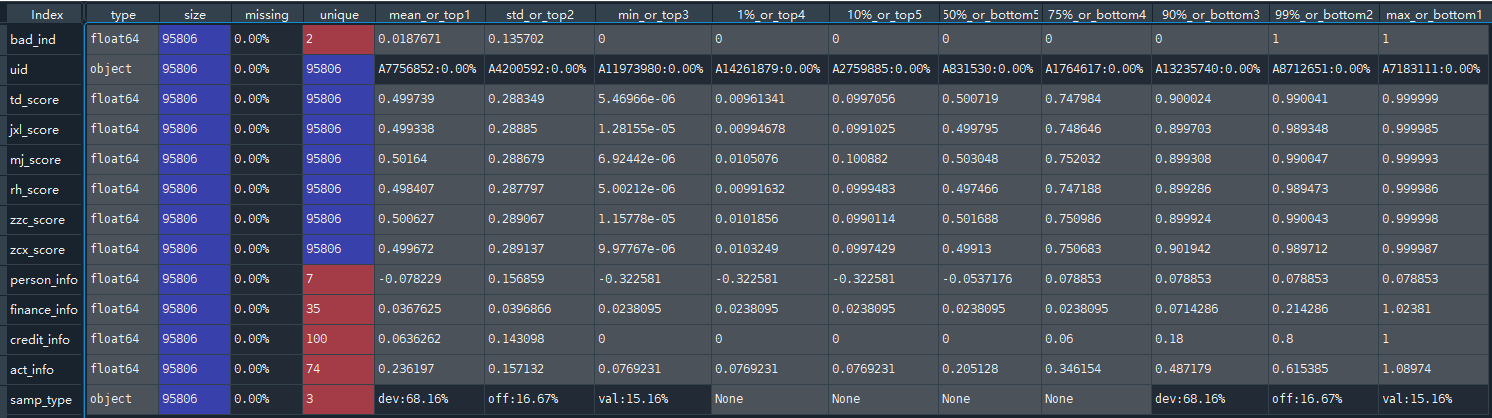
3、特征挖掘
注:Toad可以用来过滤大量的特征,如高缺失率、低iv和高度相关的特征。它还可以使用各种分箱技巧进行分箱和实现WOE转化。
计算IV、gini、entropy:
# 计算IV的快捷方法
# toad.quality(dataframe, target):返回每个特征的质量,包括iv、基尼系数和熵。可以帮助我们发现更有用的潜在信息。
quality = toad.quality(data_all,’bad_ind’)
quality.sort_values(‘iv’,ascending=False)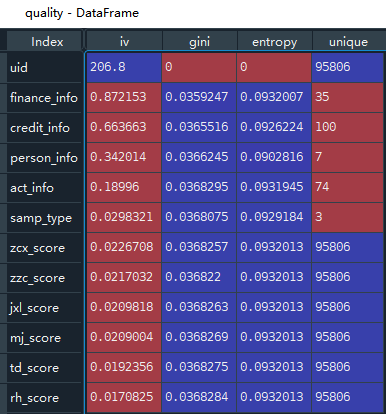
下面以缺失率大于0.7,IV值小于0.03,相关性大于1(保留更多的特征)来进行特征筛选(剔除不符合这些条件的 或的逻辑剔除,不满足其中一个均会剔除)。【其实corr=0.7更好,可以去掉有多重共线性的变量,即vif>10】
dev_slct1, drop_lst = toad.selection.select(dev, dev[‘bad_ind’],
empty=0.7, iv=0.03,
corr=1,
return_drop=True,
exclude=ex_list)
print(‘keep:’, dev_slct1.shape[1],
‘drop empty:’, len(drop_lst[‘empty’]),
‘drop iv:’, len(drop_lst[‘iv’]),
‘drop corr:’, len(drop_lst[‘corr’]))
>>keep: 12 drop empty: 0 drop iv: 1 drop corr: 0
#结果剔除了 1个变量:rh_score (因为IV不合格,iv<0.03了)
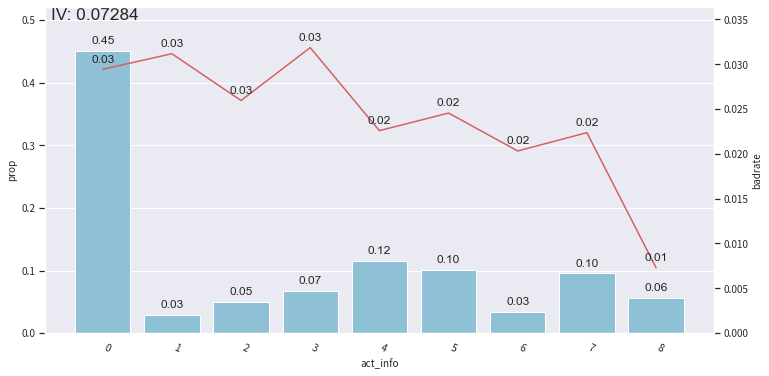
再根据卡方分箱的结果看IV:
bin_plot(dev_slct2, x=’act_info’, target=’bad_ind’) # toad.plot.bin_plot 可以看分箱后结果的IV 在图片上显示
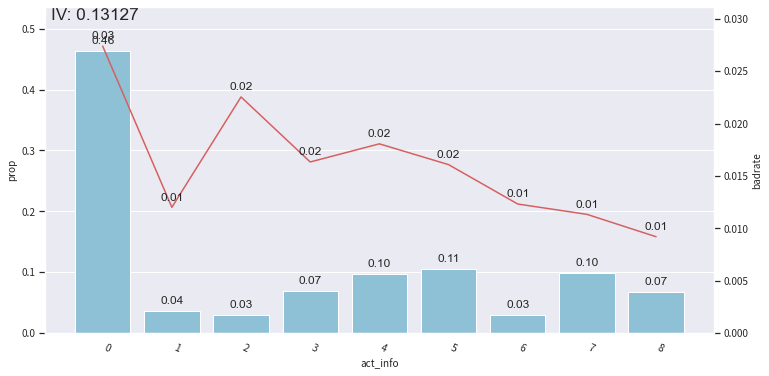
bin_plot(val2, x=’act_info’, target=’bad_ind’)
bin_plot(off2, x=’act_info’, target=’bad_ind’)
在不同样本中看变量的IV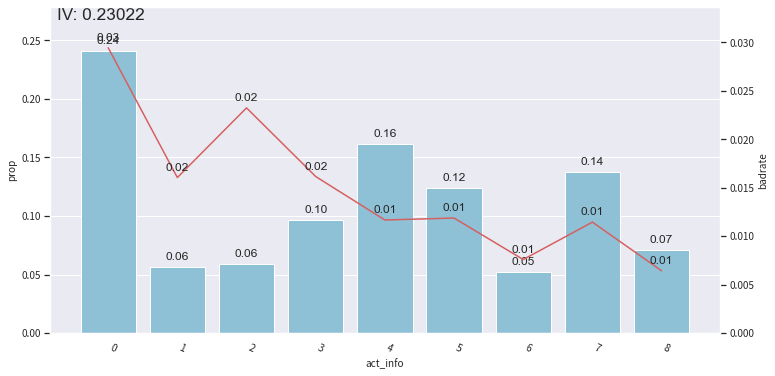
还可以调整分箱节点: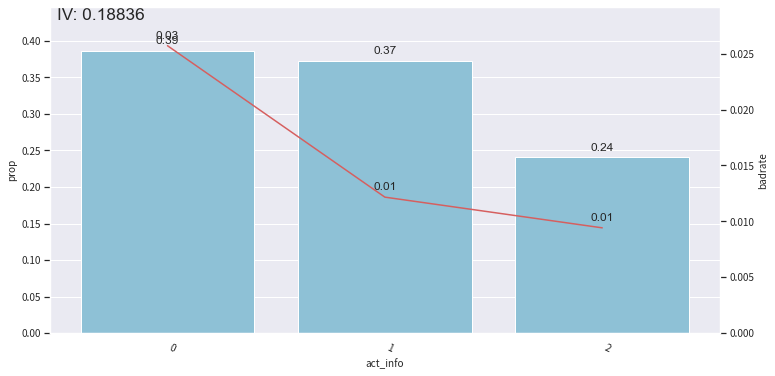
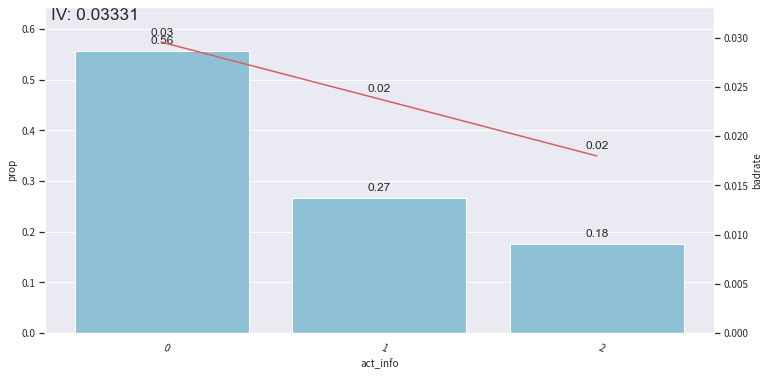
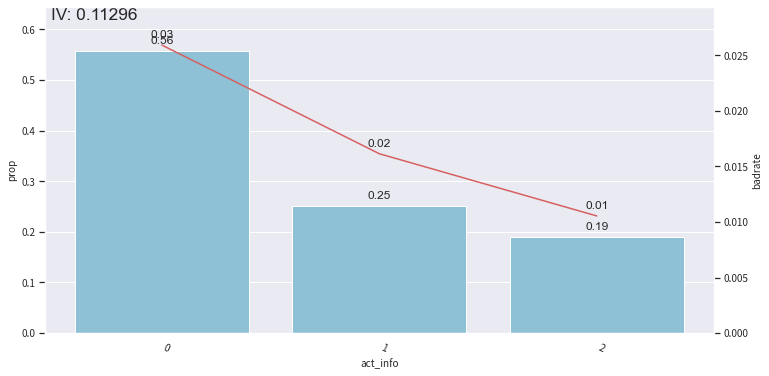
根据PSI再剔除:
筛选PSI值小于0.13的值
psi_df = toad.metrics.PSI(dev_slct2_woe, val_woe).sort_values(0)
psi_df = psi_df.reset_index()
psi_df.columns = [‘feature’, ‘psi’]
psi_013 = list(psi_df[psi_df.psi<0.13].feature)
再重新选择特征:
dev_woe_psi2, drop_lst = toad.selection.select(dev_woe_psi,
dev_woe_psi[‘bad_ind’],
empty=0.6,
iv=0.001,
corr=0.5,
return_drop=True,
exclude=ex_list)
print(‘keep:’, dev_woe_psi2.shape[1],
‘drop empty:’, len(drop_lst[‘empty’]),
‘drop iv:’, len(drop_lst[‘iv’]),
‘drop corr:’, len(drop_lst[‘corr’]))
# keep: 7 drop empty: 0 drop iv: 4 drop corr: 0 根据PSI稳定性 去掉4个变量
再根据缺失值、iv、相关性条件去判断,最终保留变量:’uid’, ‘samp_type’, ‘zcx_score’, ‘bad_ind’, ‘credit_info’, ‘act_info’, ‘person_info’
再根据逐步回归剔除变量:
dev_woe_psi_stp = toad.selection.stepwise(dev_woe_psi2,
dev_woe_psi2[‘bad_ind’],
exclude=ex_list,
direction=’both’,
criterion=’aic’,
estimator=’ols’,
intercept=False)
val_woe_psi_stp = val_woe_psi[dev_woe_psi_stp.columns]
off_woe_psi_stp = off_woe_psi[dev_woe_psi_stp.columns]
data = pd.concat([dev_woe_psi_stp, val_woe_psi_stp, off_woe_psi_stp])
print(data.shape) # (95806, 6) 又剔除一个变量 zcx_score
最后的6个变量[‘uid’, ‘samp_type’, ‘bad_ind’, ‘credit_info’, ‘act_info’, ‘person_info‘],仅最后三个为X变量
4、生成二分类模型
回归模型、xgboost模型 见代码
5、计算各模型在各样本的表现 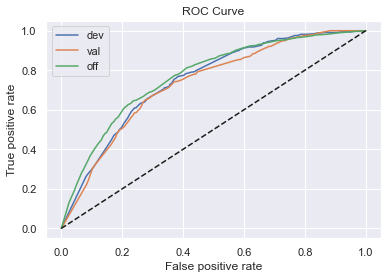
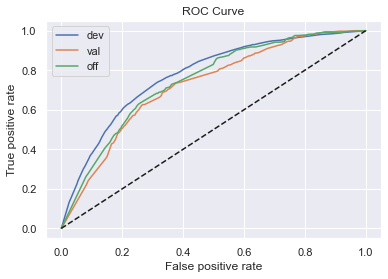
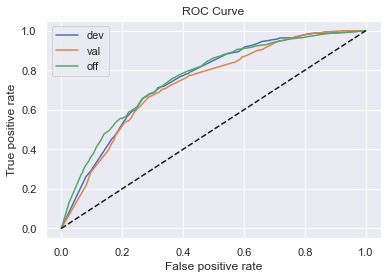
调用变量的结果:
# 结果
# 逻辑回归正向:
# train_ks: 0.4175617517173731
# val_ks: 0.3588328912466844
# off_ks: 0.36930421478753034
# 逻辑回归反向:
# train_ks: 0.38527996483390414
# val_ks: 0.37396631393463364
# off_ks: 0.40858234950836764
# XGBoost正向:
# train_ks: 0.4237042266146137
# val_ks: 0.3595635995538518
# off_ks: 0.37518296190183736
# XGBoost反向:
# train_ks: 0.3938834608675862
# val_ks: 0.37747626322745126
# off_ks: 0.39338531134694127
效果都还可以,KS基本在0.4左右
计算F1分数、KS值和AUC值:
prob_dev = lr.predict_proba(x)[:,1]
print(‘训练集’)
print(‘F1:’, F1(prob_dev,y))
print(‘KS:’, KS(prob_dev,y))
print(‘AUC:’, AUC(prob_dev,y))
# 训练集
# F1: 0.029351208260445533
# KS: 0.4175617517173731
# AUC: 0.7721143736676812
6、生成模型报告并制作评分卡
# 生成模型时间外样本的KS报告
toad.metrics.KS_bucket(prob_off,offy,
bucket=10,
method=’quantile’)
# 制作评分卡
card = ScoreCard(combiner=combiner,
transer=t, C=0.1,
class_weight=’balanced’,
base_score=600,
base_odds=35,
pdo=60,
rate=2)
card.fit(x,y)
final_card = card.export(to_frame=True) # 输出每个变量得分的情况
print(final_card)
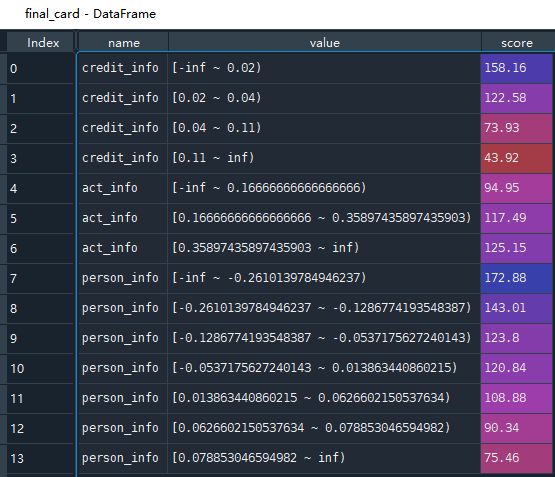
得到这三个变量的具体值对应的得分,这样一个简易的评分卡就完成了。
代码:
# -*- coding: utf-8 -*-"""Created on Fri Mar 25 09:26:19 2022@author: yingtao.xiang"""# 1.加载库# 导入基本库import warningswarnings.filterwarnings('ignore')import mathimport matplotlibimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdimport toadfrom toad.plot import bin_plot, badrate_plotfrom toad.metrics import KS, F1, AUCfrom toad.scorecard import ScoreCard# 导入算法相关库import xgboost as xgbfrom sklearn.metrics import roc_auc_score, roc_curve, aucfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionfrom sklearn.preprocessing import StandardScaler# 2.加载数据# 加载数据data_all = pd.read_csv(r'C:\Users\yingtao.xiang\Desktop\风控模型\CREDIT_SCORING_CARD_MODEL-master\CREDIT_SCORING_CARD_MODEL-master\v1/data/scorecard.txt')# 指定不参与训练列名ex_list = ['uid', 'samp_type', 'bad_ind']# 看下总样本及好坏样本数# data_all['bad_ind'].value_counts() # 一共95806个用户# 0.0 94008# 1.0 1798# Name: bad_ind, dtype: int64# 参与训练列名 共10个变量ft_list = data_all.columns.tolist()for col in ex_list:ft_list.remove(col)# 3.划分开发样本、验证样本与时间外样本 7:1.5:1.5dev = data_all[(data_all['samp_type'] == 'dev')] # 65304val = data_all[(data_all['samp_type'] == 'val')] # 14527off = data_all[(data_all['samp_type'] == 'off')] # 15975# 4.探索性数据分析toad.detector.detect(data_all) # 观测数据的缺失情况、具体的值类别、均值、标准差、分位数、最大最小等# 5.特征剔除 #剔除条件可配置dev_slct1, drop_lst = toad.selection.select(dev, dev['bad_ind'],empty=0.7, iv=0.03,corr=1,return_drop=True,exclude=ex_list)# dev_slct1, drop_lst = toad.selection.select(dev, dev['bad_ind'],# empty=0.7, iv=0.1,# corr=1,# return_drop=True,# exclude=ex_list)print('keep:', dev_slct1.shape[1],'drop empty:', len(drop_lst['empty']),'drop iv:', len(drop_lst['iv']),'drop corr:', len(drop_lst['corr']))#结果剔除了 1个变量:rh_score# 6.卡方分箱# 得到切分节点combiner = toad.transform.Combiner()combiner.fit(dev_slct1, dev_slct1['bad_ind'], method='chi',min_samples=0.05, exclude=ex_list)# 导出箱的节点bins = combiner.export()print(bins)# 7.分箱效果图# 根据节点实施分箱dev_slct2 = combiner.transform(dev_slct1) # 计算每个用户具体值在每一个箱体位置val2 = combiner.transform(val[dev_slct1.columns])off2 = combiner.transform(off[dev_slct1.columns])# 分箱后通过画图观察# 使用bad_rate验证分箱在测试集或者跨时间验证集上的稳定性# 使用bad_rate验证分箱在测试集或者跨时间验证集上的稳定性# 使用bad_rate验证分箱在测试集或者跨时间验证集上的稳定性bin_plot(dev_slct2, x='act_info', target='bad_ind') # toad.plot.bin_plot 可以看分箱后结果的IV 在图片上显示bin_plot(val2, x='act_info', target='bad_ind') # toad库 评分卡模型很赞bin_plot(off2, x='act_info', target='bad_ind')# 查看单箱节点bins['act_info']# 只保留需要的两个分割点,并重新画出Bivar图 #进行调整 只分2个节点,三个箱体adj_bin = {'act_info': [0.16666666666666666, 0.35897435897435903,]}combiner.set_rules(adj_bin)dev_slct3 = combiner.transform(dev_slct1)val3 = combiner.transform(val[dev_slct1.columns])off3 = combiner.transform(off[dev_slct1.columns])# 画出bin_plot(dev_slct3, x='act_info', target='bad_ind')bin_plot(val3, x='act_info', target='bad_ind')bin_plot(off3, x='act_info', target='bad_ind')# 8.绘制负样本占比关联图# 无错位data = pd.concat([dev_slct3, val3, off3], join='inner')# 画出不同数据集的每一箱的bad_rate图。这里可以是训练集测试集,也可以不同月份的对比。by后面是纵轴。x是需要对比的维度,比如训练集测试集、不同的月份。badrate_plot(data, x='samp_type', target='bad_ind', by='person_info')badrate_plot(dev_slct3, x='samp_type', target='bad_ind', by='person_info')# 9.WOE编码t = toad.transform.WOETransformer()dev_slct2_woe = t.fit_transform(dev_slct3, dev_slct3['bad_ind'], exclude=ex_list)val_woe = t.transform(val3[dev_slct3.columns])off_woe = t.transform(off3[dev_slct3.columns])data = pd.concat([dev_slct2_woe, val_woe, off_woe])# 10.筛选PSI值小于0.13的值psi_df = toad.metrics.PSI(dev_slct2_woe, val_woe).sort_values(0)psi_df = psi_df.reset_index()psi_df.columns = ['feature', 'psi']psi_013 = list(psi_df[psi_df.psi<0.13].feature)for i in ex_list:if i in psi_013:passelse:psi_013.append(i)data = data[psi_013]dev_woe_psi = dev_slct2_woe[psi_013]val_woe_psi = val_woe[psi_013]off_woe_psi = off_woe[psi_013]print(data.shape)# 计算训练集与时间外验证样本的PSI,删除PSI大于0.13的特征。注意,通过单个特征的PSI值建议在0.02以下,根据具体情况可以适当调整。# 11.重新选择特征dev_woe_psi2, drop_lst = toad.selection.select(dev_woe_psi,dev_woe_psi['bad_ind'],empty=0.6,iv=0.001,corr=0.5,return_drop=True,exclude=ex_list)print('keep:', dev_woe_psi2.shape[1],'drop empty:', len(drop_lst['empty']),'drop iv:', len(drop_lst['iv']),'drop corr:', len(drop_lst['corr']))# keep: 7 drop empty: 0 drop iv: 4 drop corr: 0 根据PSI稳定性 去掉4个变量# 12.逐步回归dev_woe_psi_stp = toad.selection.stepwise(dev_woe_psi2,dev_woe_psi2['bad_ind'],exclude=ex_list,direction='both',criterion='aic',estimator='ols',intercept=False)val_woe_psi_stp = val_woe_psi[dev_woe_psi_stp.columns]off_woe_psi_stp = off_woe_psi[dev_woe_psi_stp.columns]data = pd.concat([dev_woe_psi_stp, val_woe_psi_stp, off_woe_psi_stp])print(data.shape) # (95806, 6)# 13.模型训练# 13.1.定义逻辑回归函数def lr_model(x, y, valx, valy, offx, offy, C):model = LogisticRegression(C=C, class_weight='balanced')model.fit(x, y)y_pred = model.predict_proba(x)[:,1]fpr_dev, tpr_dev, _ = roc_curve(y, y_pred)train_ks = abs(fpr_dev - tpr_dev).max()print('train_ks: ', train_ks)y_pred = model.predict_proba(valx)[:,1]fpr_val, tpr_val, _ = roc_curve(valy, y_pred)val_ks = abs(fpr_val - tpr_val).max()print('val_ks: ', val_ks)y_pred = model.predict_proba(offx)[:,1]fpr_off, tpr_off, _ = roc_curve(offy, y_pred)off_ks = abs(fpr_off - tpr_off).max()print('off_ks: ', off_ks)plt.plot(fpr_dev, tpr_dev, label='dev')plt.plot(fpr_val, tpr_val, label='val')plt.plot(fpr_off, tpr_off, label='off')plt.plot([0,1], [0,1], 'k--')plt.xlabel('False positive rate')plt.ylabel('True positive rate')plt.title('ROC Curve')plt.legend(loc='best')plt.show()# 13.2.定义XGBoost函数def xgb_model(x, y, valx, valy, offx, offy):model = xgb.XGBClassifier(learning_rate=0.05,n_estimators=400,max_depth=2,class_weight='balanced',min_child_weight=1,subsample=1,nthread=-1,scale_pos_weight=1,random_state=1,n_jobs=-1,reg_lambda=300)model.fit(x, y)y_pred = model.predict_proba(x)[:,1]fpr_dev, tpr_dev, _ = roc_curve(y, y_pred)train_ks = abs(fpr_dev - tpr_dev).max()print('train_ks: ', train_ks)y_pred = model.predict_proba(valx)[:,1]fpr_val, tpr_val, _ = roc_curve(valy, y_pred)val_ks = abs(fpr_val - tpr_val).max()print('val_ks: ', val_ks)y_pred = model.predict_proba(offx)[:,1]fpr_off, tpr_off, _ = roc_curve(offy, y_pred)off_ks = abs(fpr_off - tpr_off).max()print('off_ks: ', off_ks)plt.plot(fpr_dev, tpr_dev, label='dev')plt.plot(fpr_val, tpr_val, label='val')plt.plot(fpr_off, tpr_off, label='off')plt.plot([0,1], [0,1], 'k--')plt.xlabel('False positive rate')plt.ylabel('True positive rate')plt.title('ROC Curve')plt.legend(loc='best')plt.show()# 13.3.调用模型def bi_train(data, dep='bad_ind', exclude=None):std_scaler = StandardScaler()# 变量名lis = data.columns.tolist()for i in exclude:lis.remove(i)data[lis] = std_scaler.fit_transform(data[lis])devv = data[(data['samp_type'] == 'dev')]vall = data[(data['samp_type'] == 'val')]offf = data[(data['samp_type'] == 'off')]x, y = devv[lis], devv[dep]valx, valy = vall[lis], vall[dep]offx, offy = offf[lis], offf[dep]# 逻辑回归正向print('逻辑回归正向:')lr_model(x, y, valx, valy, offx, offy, 0.1)# 逻辑回归反向print('逻辑回归反向:')lr_model(offx, offy, valx, valy, x, y, 0.1)# XGBoost正向print('XGBoost正向:')xgb_model(x, y, valx, valy, offx, offy)# XGBoost反向xgb_model(offx, offy, valx, valy, x, y)bi_train(data, dep='bad_ind', exclude=ex_list)# 结果# 逻辑回归正向:# train_ks: 0.41733648227995124# train_ks: 0.3593935758405114# train_ks: 0.3758086175640308# 逻辑回归反向:# train_ks: 0.3892612859630226# train_ks: 0.3717891855920369# train_ks: 0.4061965880072622# XGBoost正向:# [23:20:46] WARNING: C:\Users\Administrator\workspace\xgboost-win64_release_1.2.0\src\learner.cc:516:# Parameters: { class_weight } might not be used.# This may not be accurate due to some parameters are only used in language bindings but# passed down to XGBoost core. Or some parameters are not used but slip through this# verification. Please open an issue if you find above cases.# train_ks: 0.42521927400747045# train_ks: 0.3595542266920359# train_ks: 0.37437103192850807# [23:20:48] WARNING: C:\Users\Administrator\workspace\xgboost-win64_release_1.2.0\src\learner.cc:516:# Parameters: { class_weight } might not be used.# This may not be accurate due to some parameters are only used in language bindings but# passed down to XGBoost core. Or some parameters are not used but slip through this# verification. Please open an issue if you find above cases .# train_ks: 0.3939473708822855# train_ks: 0.3799497614606668# train_ks: 0.3936270948436908# 14.单个逻辑回归模型进行拟合dep = 'bad_ind'lis = list(data.columns)for i in ex_list:lis.remove(i)devv = data[data['samp_type']=='dev']vall = data[data['samp_type']=='val']offf = data[data['samp_type']=='off' ]x, y = devv[lis], devv[dep]valx, valy = vall[lis], vall[dep]offx, offy = offf[lis], offf[dep]lr = LogisticRegression()lr.fit(x, y)# 15.计算F1分数、KS值和AUC值prob_dev = lr.predict_proba(x)[:,1]print('训练集')print('F1:', F1(prob_dev,y))print('KS:', KS(prob_dev,y))print('AUC:', AUC(prob_dev,y))# 训练集# F1: 0.029351208260445533# KS: 0.4175617517173731# AUC: 0.7721143736676812prob_val = lr.predict_proba(valx)[:,1]print('验证集')print('F1:', F1(prob_val,valy))print('KS:', KS(prob_val,valy))print('AUC:', AUC(prob_val,valy))# 验证集# F1: 0.03797468354430379# KS: 0.3588328912466844# AUC: 0.7222256797668032prob_off = lr.predict_proba(offx)[:,1]print('跨时间')print('F1:', F1(prob_off,offy))print('KS:', KS(prob_off,offy))print('AUC:', AUC(prob_off,offy))# 跨时间# F1: 0.022392178506662464# KS: 0.3696948842371405# AUC: 0.7436315034285385# 从两个角度衡量稳定性,分别计算模型PSI和单变量PSIprint('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))print('特征PSI:','\n',toad.metrics.PSI(x,offx).sort_values(0))# 模型PSI: 0.33682698167332736# 特征PSI:# credit_info 0.098585# act_info 0.122049# person_info 0.127833# dtype: float64# 生成模型时间外样本的KS报告toad.metrics.KS_bucket(prob_off,offy,bucket=10,method='quantile')# toad.metrics.KS_bucket(prob_val,valy,# bucket=10,# method='quantile')# toad.metrics.KS_bucket(prob_dev,y,# bucket=10,# method='quantile')# 制作评分卡card = ScoreCard(combiner=combiner,transer=t, C=0.1,class_weight='balanced',base_score=600,base_odds=35,pdo=60,rate=2)card.fit(x,y)final_card = card.export(to_frame=True) # 输出每个变量得分的情况print(final_card)

