相对熵与IV、PSI的关系

最近在读《Python金融大数据风控建模实战》这本书，读的过程中发现很多有意思的地方，所以准备最近对这本书中的一些理论知识做一些记录，将一个个知识点串起来，也加深一下自己对模型的理解。

目录

1. 相对熵(K-L散度)
2. 相对熵与IV的关系
3. 相对熵与PSI的关系
4. 参考资料

一、相对熵
概率是表征随机变量确定性的度量，而信息是随机变量不确定性的度量，熵就是不确定性度量的平均值，即为信息的平均值。熵有很多种类型，比如信息熵、条件熵、交叉熵等。以交叉熵为例，假设随机变量的真实分布为p，预测分布为q，交叉熵度量了从q到p还需要的信息量。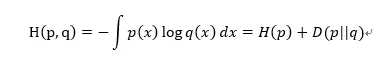

H(p,q)为从q到p的交叉熵，H(p)为分布p的信息熵，D(p||q)为相对熵，也就是K-L散度。它是两个随机分布之间距离的度量，是衡量两个概率密度函数独立性的指标。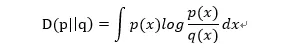

注意一点，K-L散度没有对称性，即D(p||q)≠D(q|p)，这意味着K-L散度是单向描述信息熵差异。因此如果将两个随机分布之间的K-L散度求和，这个求和后的距离越大，证明两个随机分布的距离越大。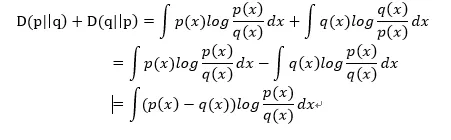

因此就得到一个具有对称性的距离，即为K-L距离。在数学上的距离需要满足：非负性、对称性、同一性、传递性等，因此可以理解为K-L散度不是距离，但是两个K-L散度之和可以叫做K-L距离，因为满足了对称性的要求。
为了便于理解，下面用一个案例介绍相对熵如何计算(案例来源于群体稳定性指标(PSI)深入理解)。假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。通过观察，得到概率分布B与C，各个分布的具体情况如下：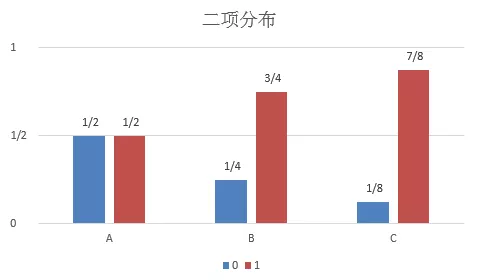

可以计算出得到KL散度如下：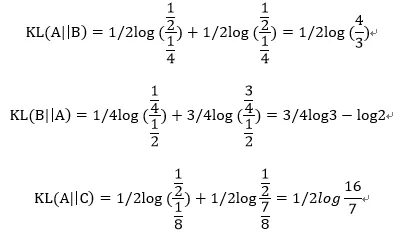

由上式可知，相对熵KL(A||C) > KL(A||B)，说明A和B之间的概率分布在信息量角度更为接近。而通过概率分布可视化观察，我们也认为A和B更为接近，两者吻合。

二、相对熵与IV的关系
将上述中的K-L距离中的两个随机分布p、q换为模型预测后得到的正负样本的概率密度函数f(p|B)和f(p|G)，得到如下公式: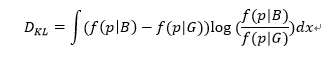

如果将上式写成离散形式，则连续变量分箱后的形式为：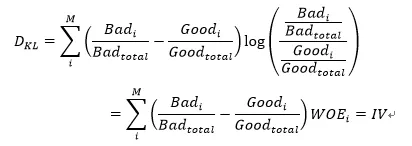

因此，对称化后的K-L距离就是IV值。所以在挑选变量时，在每个区间的IV值越大，就表示在这个区间正负样本的概率密度函数f(p|B)与f(p|G)的距离就越大，在该区间内变量对好坏样本的区分度就越高。

三、相对熵与PSI的关系
PSI计算公式及变形如下：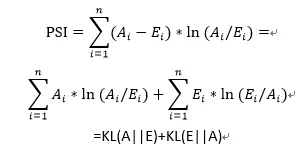

因此，PSI本质上是实际分布（A）与预期分布（E）的K-L散度的一个对称化操作。其双向计算相对熵，并把两部分相对熵相加，从而更为全面地描述两个分布的差异。
总结一下，PSI衡量预期分布和实际分布之间的差异性，用以判断变量稳定性，IV衡量好人分布和坏人分布之间的差异性，用以判断变量预测能力，其背后的支撑理论都是相对熵。

四、参考资料

1. 《Python金融大数据风控建模实战》
2. WOE与IV指标的深入理解应用
3. 群体稳定性指标(PSI)深入理解应用