全文共3673字,阅读全文预计需9分钟。
什么是贝塞尔曲线
贝塞尔曲线最早于1962年由法国工程师皮埃尔·贝塞尔(Pierre Bézier)发表,应用于汽车设计。而后作为重要的曲线之一,被广泛应用于计算机图形学。作为前端开发,熟悉的 css 动画、数据可视化等领域,都可以看到贝塞尔曲线的应用。
贝塞尔曲线可以概括为:由 n 个定点按顺序得到的 n-1 条连线,通过在连线中以相同比例 t(t 在[0, 1] 的范围间) 在不同线段中的位置得到的关于 t 的点的集合,得到一个运动轨迹,这个轨迹就是贝塞尔曲线。简单来说就是, 通过给定的点,按一定的关系,得到的一条曲线。
在贝塞尔曲线中,我们通过定点( 这些定点,称为控制点 )连接得到的线段数量来划分阶数。下面用简单的例子来稍微解释一下。
一阶曲线
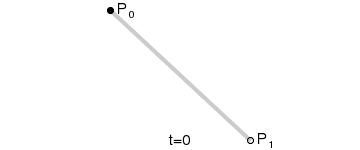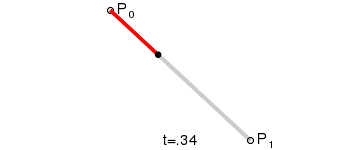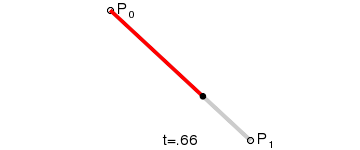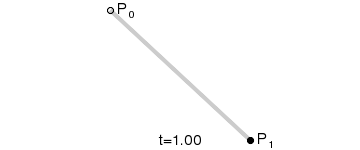
又称线性曲线,如图所示,是由给点 P0 和 P1 得到的关于 t 的运动轨迹,比如,t=0.25时,B(t) 就等于 P0 到 P1 这条路径的四分之一。由于两点只能确定一条直线,因此路径表现也是一条直线。
二阶曲线
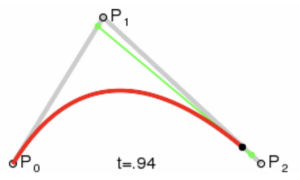
已知 P0、P1、P2 三个定点,通过数学关系得到了一条关于 t 的运动轨迹,也就是红色曲线。如图所示:
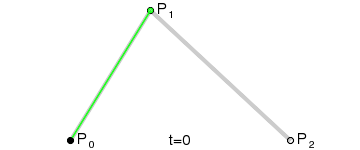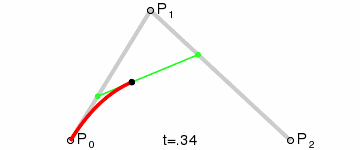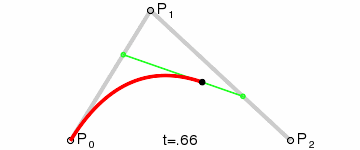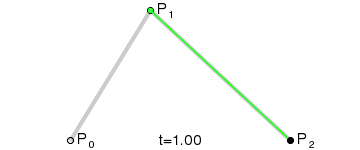
那么这条曲线是如何得到的呢?
- 假设 t = 0.25,分别在 P0P1 线段和 P1P2 线段中分别找到对应的点 A、B,使 P0A : P0P1 = P1B : P1P2 = 0.25,位置如下所示。
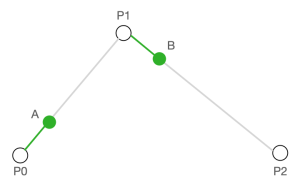
- 将点 A、B 进行连线,并在线段 AB 中同样找到一个点 C,使 AC : AB = 0.25,此时点 C 则是点 P0、P1、P2 决定的贝塞尔曲线上 t = 0.25 的轨迹点。
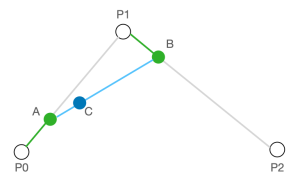
- 同步骤 1,找到点 A’、B’ ,使 P0A’ : P0P1 = P1B’ : P1P2 = 0.5;再同步骤 2,在线段 A’B’ 中找到 C’,使 A’C’ : A’B’ = 0.5,此时点 C’ 则是点 P0、P1、P2 决定的贝塞尔曲线上 t = 0.5 的轨迹点。
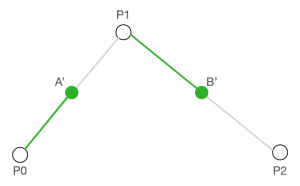
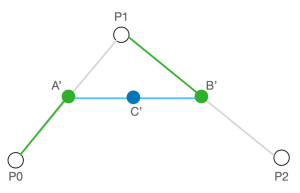
- 当我们把 t 在 [0, 1] 范围中每个值对应的轨迹点连接起来时,便可以得到这条红色的贝塞尔曲线。
三阶曲线
三阶曲线,则是通过点 P0、P1、P2、P3 及构成的三条线段所得到的一条曲线。
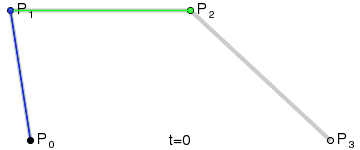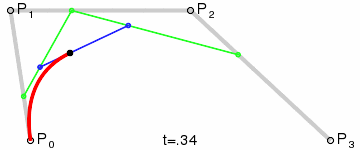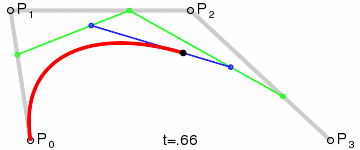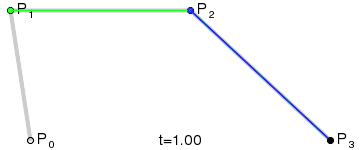
了解完二阶曲线是如何通过给定的控制点得到贝塞尔曲线,当控制点增加一个后,又是如何获取轨迹点的呢?
- 和二阶曲线一样,假设 t = 0.25,我们先在四个控制点组成的三条线段中分别找到点 A、B、C,使得 P0A : P0P1 = P1B : P1P2 = P2C : P2P3 = 0.25。
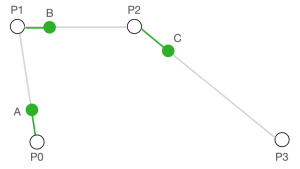
- 连接 A、B 和 B、C,并在线段 AB、BC 中分别找到点 D、E,使 AD : AB = BE : BC = 0.25。
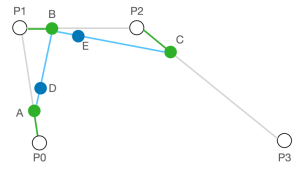
- 再连接 D、E,于线段 DE 中取点 F,使 DF : DE = 0.25。此时点 C 则是点 P0、P1、P2、P3 决定的贝塞尔曲线上 t = 0.25 的轨迹点。
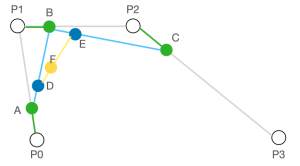
- 同理,得到 t = 0.5 时,点 P0、P1、P2、P3 决定的贝塞尔曲线上 t = 0.5 的轨迹点 F’。
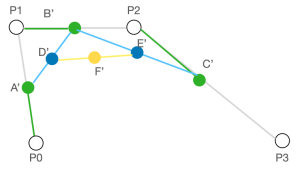
- 连接 t 在 [0, 1] 范围的所有轨迹点,得到红色的贝塞尔曲线。
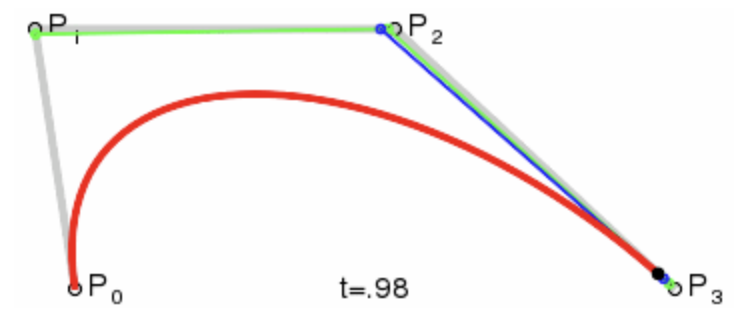
四阶及以上的高阶曲线
通过二阶、三阶贝塞尔曲线的推导,我们可以得出,轨迹点的计算,本质上就是递归, 通过不断地计算线段中符合比例 t 的点,得到最终的一个点,这个点就是当前曲线在当前比例 t 的轨迹点。那么就可以得到 n 阶贝塞尔曲线的推导公式:
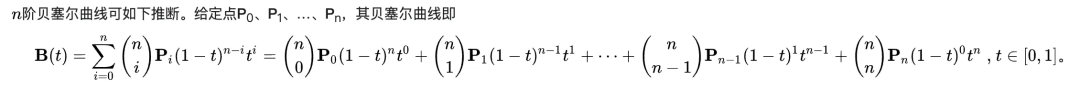
在前端中,熟悉的 css3 transition-timing-function 函数(缓动函数),比如 ease、ease-in 等,就是通过三阶贝塞尔曲线来描绘其动画速度变化。
笔者参与的可视化项目中,有一个智能色彩工具,可以通过给定的输入色和风格,经过算法计算,智能生成一组随机的配色色板,可用于可视化、UI的配色。
需要进一步优化
于我而言,由工具生成的色板已经满足了我日常项目的配色需求。
但仍存在一些细节问题,其中一个就是:部分颜色色阶划分不均匀。如下:

可以看到,这两个颜色生成的色阶,部分色阶区分度不大,出现了粘滞或者过大。当色阶划分不均匀,相邻色阶区分度不高的时候,可能会有这些问题:
● 可视化领域中,色阶区分度不高,会引起误读。比如热力图,当相邻色阶之间区分度较小时,在阅读图表时,不能直观地感知到数据的差异
● 应用于 UI 配色时,可能会导致组件不同状态的配色相近,如按钮常态和 hover 态颜色相近,hover 效果不明显
● 等等……
在对于色阶优化的探索中,我们把目光对准了业内最新的色彩模型,来自 Google 的 HCT 色彩模型。它是基于 CAM16 模型建立,更具有人眼感知均匀性的色域空间,这从根本上对色彩均匀度进行了优化。但由于这涉及到色彩空间这种专业理论,不属于本文涉及的范畴,暂不展开。
在最初对色阶进行划分规则制定的过程,我们期望可以简单地将每一级对应的亮度量化成如同 10、20、30……80、90、100 这样偏线性的规律。但在色彩空间来说,无论使用什么样的模型,色彩的变化都不会是一个线性规律。亮度在明暗两端,相比于中间段的色彩,在人眼能感知的感官差异中,需要的数值变化更小。 因此我们需要通过若干特征点,建立曲线来描述这个变化规律,并能准确应用到不同数量的色阶划分中。
那么,什么样的曲线,才能得到一个过渡平滑、令人观感舒适的色阶呢?
灵感
偶然了解了胶片摄影,由于独特的色彩和感光度,形成了一种别样的风格,吸引着许多摄影爱好者。胶片中存在一个胶片特性曲线(HD曲线),是测量摄影胶卷感光性的感光曲线。
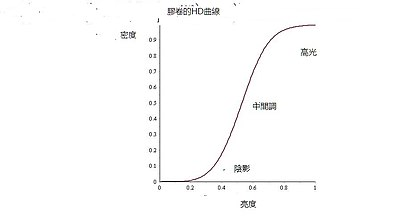
通过曲线可以看到,亮度变化中,明暗两端并非是线性关系,而是趋于平缓。在摄影后期调色中,很多人会参考这个曲线,调整整体影调,来达到比较有层次感但又过渡比较平滑的色调。
那么,我们是否能参考这个特性,在色阶划分中尝试找到一个新的思路呢?
回归到色阶的问题, 我们需要一个曲线关系,能够把感性的、符合审美标准的色阶,将其每一阶的亮度分布进行量化。于是我们找到了贝塞尔曲线作为答案。
可行性
在通过对业内一些相似的产品进行分析,其中可以看到贝塞尔曲线应用在色彩领域的身影。比如 ColorBox,可以通过贝塞尔曲线,在色相、饱和度、亮度进行划分;在 Ant Design 之前的色板当中,也可以看到他们是通过一个固定的贝塞尔曲线,生成一组亮度值。
正如前文提及,前端有一些常见的缓动函数应用于 css 动画中。我们尝试将它们应用在色阶划分中,整体设计方案就是:通过给定的贝塞尔曲线,根据用户输入的色阶个数 n,在 t 的范围区间 [0, 1] 划分成 n 个刻度,将每个 t 取值对应的 B(t) 通过一定的转换关系映射到对应位置的色阶当中。
举个例子,如下图所示:
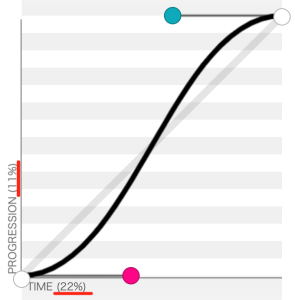
假设 n = 10,当十个色阶的第二阶,即 t = 2 * (n - 1) = 0.22 时,B(t) = 0.11,将 0.11 作为第二个色阶的 Tone 值。依次类推,色阶上每个颜色的亮度值都能分布在曲线上,这样色阶就能按曲线的增长趋势来分布。
当然,实际应用过程中,并非直接将曲线等分映射到亮度中,因为非中性色的色阶生成中,过暗和过亮的颜色观感上美观性不足,因此需要对这两端进行裁剪,那么亮度就存在了一个范围区间。我们考虑了两种模式:曲线缩放和区间缩放。
● 曲线缩放,是将曲线根据范围的变化进行伸缩变形
● 区间缩放,是指将区间作为曲线上的一个滑动窗口,以截取区间内的曲线
举个例子,假如定义的亮度区间是 12~96,曲线缩放就是在 12 和 96 之间找到一组符合既定曲线变化趋势的亮度值;而区间缩放则是,在原来的曲线中,截取 12~96 这部分变化趋势。
对于贝塞尔曲线的阶数,一开始我们考虑了通过一些关键值,找到一组曲线通过这些点,以得到一个固定的高阶贝塞尔曲线。但在预研阶段,相比于三阶曲线,高阶虽然有更大的灵活度,但是差异较小,并且由于计算量比三阶大,性能上也没有优势。经过测试和验证,三阶贝塞尔曲线的应用表现基本符合了设计风格的预期,能得到较好的效果。
代码
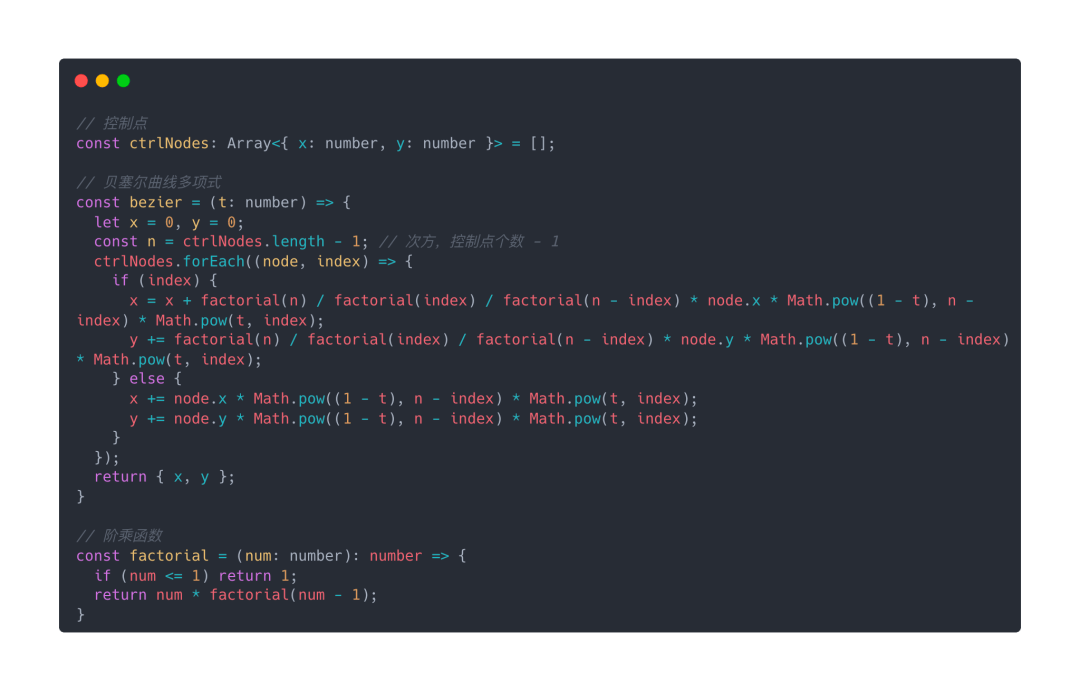
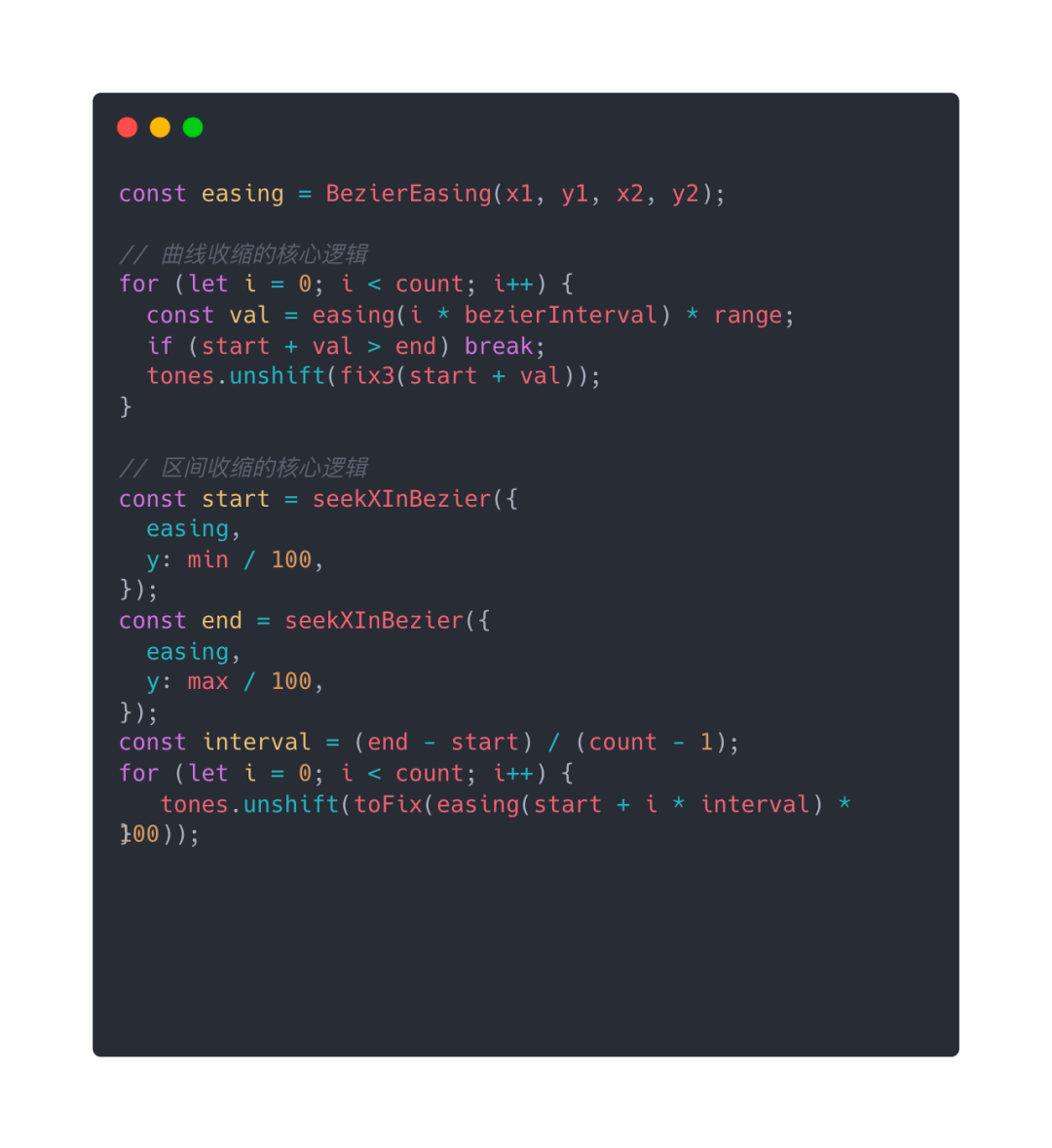
三阶贝塞尔曲线在业内已经有开源的第三方库,因此可以在项目中引入,不需要重复造轮子,比如 bezier-easing,下面用伪代码来演示:
初步成效
以前文颜色示例,以缓动函数 ease-in-out 为例,这条曲线的特征是:相比于中间段,起点和终点的变化趋势比较小。结合到色阶,效果如下:

可以看到,划分得到的色阶,呈现了预期的效果,两端的明暗度变化较小。
更进一步

通过分析,由于色彩空间中不同的色相存在不同的颜色数量,因此彼此之间不能只寄望于一个统一的变化趋势就能满足。
此外,常见的缓动函数并不足以调整到符合设计风格规范的效果。可以看到,使用 ease-in-out 生成的色阶,两端各自的颜色区分度还是比较小。在前面提到的类似产品中,ColorBox 在贝塞尔曲线的应用中,只停留在使用通用缓动函数;而 Ant Design 是根据冷暖色来分别处理。因此,我们需要根据颜色变化规律,对色相进行分类,并对不同的色相,应用不同的曲线。
参考 cubic-bezier.com 实现了一个可视化工具,借助这个工具,设计同学可以通过拖动控制点,实时观察色阶相应变化,来得到一个符合要求的自定义贝塞尔曲线。通过颜色选择器取出不同色相的颜色,以此来找到不同色相相应的贝塞尔曲线。

通过设计同学的精心调整,得到了不同的曲线和区间。
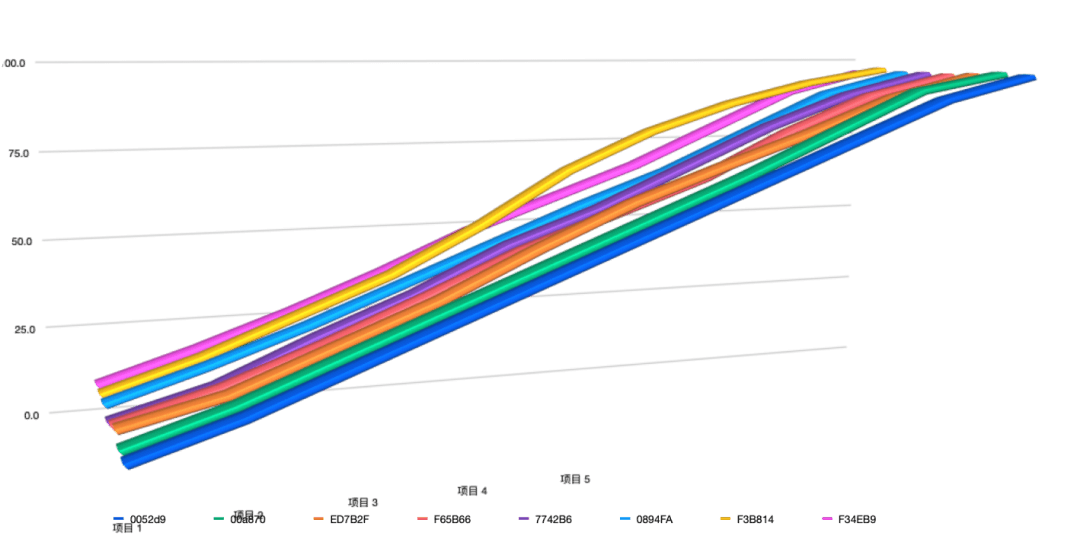
再用前面的颜色示例,来展示最新效果,依次是:旧方案、通用缓动函数方案、自定义缓动函数方案 。


尽管在这次优化中,贝塞尔曲线不是唯一解,也不一定是最优解,但对于色阶这个场景,它的特性能很好地满足我们的需求。在此之前,对贝塞尔曲线的固有印象,就是制作动效或者绘制形状。应用到色彩,于我而言是一个新的体验和尝试。它其实代表着是一种数学关系,应该还有更多可能性。
通过具象的可视化工具,每个人都可以为自己度身定制配色色板。此外,腾讯也对外开源了具备腾讯设计语言和视觉风格的图表设计资源,帮助设计师工作提效。
参考材料:
维基百科 - 贝塞尔曲线
维基百科 - HD曲线
Cubic-Bezier

