使用直方图绘制累积分布

这展示了如何绘制一个累积的、归一化的直方图作为一个步骤函数，以便可视化一个样本的经验累积分布函数(CDF)。文中还给出了理论上的CDF值。

演示了 hist 函数的其他几个选项。也就是说，我们使用 normed 参数来标准化直方图以及 累积 参数的几个不同选项。normed参数采用布尔值。 如果为 True ，则会对箱高进行缩放，使得柱状图的总面积为1。累积的kwarg稍微有些细微差别。与normed一样，您可以将其传递为True或False，但您也可以将其传递-1以反转分布。

由于我们显示了归一化和累积直方图，因此这些曲线实际上是样本的累积分布函数（CDF）。 在工程学中，经验CDF有时被称为“非超越”曲线。 换句话说，您可以查看给定-x值的y值，以使样本的概率和观察值不超过该x值。 例如，x轴上的值225对应于y轴上的约0.85，因此样本中的观察值不超过225的可能性为85％。相反，设置累积为-1，如同已完成 在此示例的最后一个系列中，创建“超出”曲线。

选择不同的箱数和大小会显着影响直方图的形状。Astropy文档有关于如何选择这些参数的重要部分：http://docs.astropy.org/en/stable/visualization/histogram.html

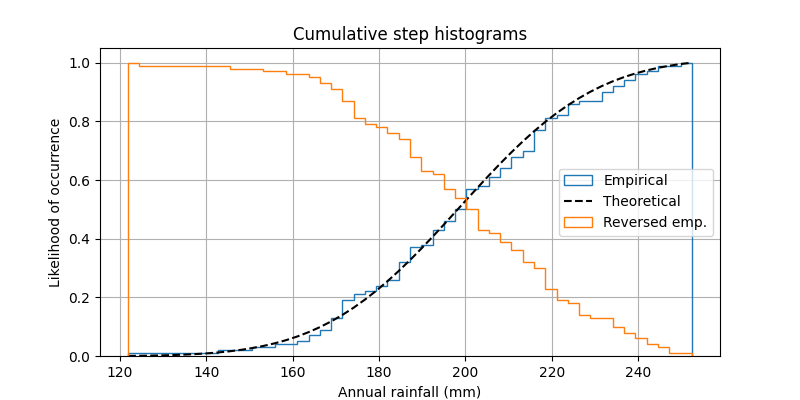
使用直方图绘制累积分布

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. np.random.seed(19680801)
  6. mu = 200
  7. sigma = 25
  8. n_bins = 50
  9. x = np.random.normal(mu, sigma, size=100)
  11. fig, ax = plt.subplots(figsize=(8, 4))
  13. # plot the cumulative histogram
  14. n, bins, patches = ax.hist(x, n_bins, density=True, histtype='step',
  15.                            cumulative=True, label='Empirical')
  17. # Add a line showing the expected distribution.
  18. y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
  19.      np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
  20. y = y.cumsum()
  21. y /= y[-1]
  23. ax.plot(bins, y, 'k--', linewidth=1.5, label='Theoretical')
  25. # Overlay a reversed cumulative histogram.
  26. ax.hist(x, bins=bins, density=True, histtype='step', cumulative=-1,
  27.         label='Reversed emp.')
  29. # tidy up the figure
  30. ax.grid(True)
  31. ax.legend(loc='right')
  32. ax.set_title('Cumulative step histograms')
  33. ax.set_xlabel('Annual rainfall (mm)')
  34. ax.set_ylabel('Likelihood of occurrence')
  36. plt.show()

下载这个示例