acwing1489. 田忌赛马（贪心）

这是中国历史上的一个著名故事。
大约 23002300 年前，田忌是齐国的一位将军，他喜欢与国王等人赛马。
田忌和国王都有三匹不同等级的马——下马、中马、上马。
规则是一场比赛要进行三个回合，每匹马进行一回合的较量，单回合的获胜者可以从失败者那里得到 200200 银元。
比赛的时候，国王总是用自己的上马对田忌的上马，中马对中马，下马对下马。
由于国王每个等级的马都比田忌的马强一些，所以比赛了几次，田忌都失败了，每次国王都能从田忌那里拿走 600600 银元。
田忌对此深感不满，直到他遇到了著名的军事家孙膑，利用孙膑给他出的主意，田忌终于在与国王的赛马中取得了胜利，拿走了国王的 200200 银元。
其实胜利的方法非常简单，他用下马对战国王的上马，上马对战国王的中马，中马对战国王的下马，这样虽然第一回合输了，但是后两回合都胜了，最终两胜一负，取得了比赛胜利。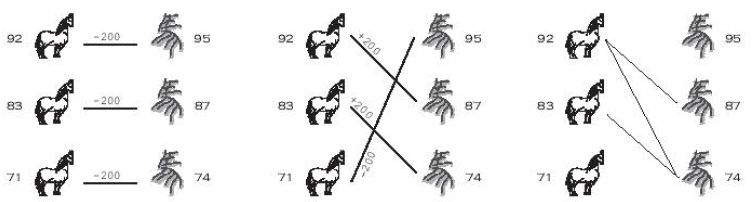

如果田忌活在如今，那么他可能会嘲笑自己当初的愚蠢。
重要的是，如果他现在正参加 ACM 竞赛，他可能会发现赛马问题可以简单地看作是在二分图中找到最大匹配项。
在一侧画田忌的马，在另一侧画国王的马，只要田忌的一匹马能够击败国王的一匹马，我们就在这两匹马之间画一条边。
然后，赢尽可能多的回合，就变成了在这个二分图中找到最大匹配。
如果存在平局，问题会变得更加复杂，他需要为所有可能的边分配权重 0、10、1 或 −1−1，并找到最大加权的完美匹配…
然而，赛马问题其实是二分图匹配的一种非常特殊的情况。
该图由马的速度决定，速度快的总是能击败速度慢的。
这种情况下，加权二分图匹配算法就显得大材小用了。
在这个问题中，你需要编写一个程序，来解决这一特殊的匹配问题。

输入格式

输入包含最多 5050 组测试数据。
每组数据第一行包含一个整数 nn，表示一方马的数量。
第二行包含 nn 个整数，是田忌的马的速度。
第三行包含 nn 个整数，是国王的马的速度。
输入的最后一行为 00，表示输入结束。

输出格式

每组数据输出一个占一行的整数，表示田忌最多可以获得多少银元。

数据范围

1≤n≤10001≤n≤1000
马的速度不超过 10001000。

输入样例：

3 92 83 71 95 87 74 2 20 20 20 20 2 20 19 22 18 0

输出样例：

200 0 0

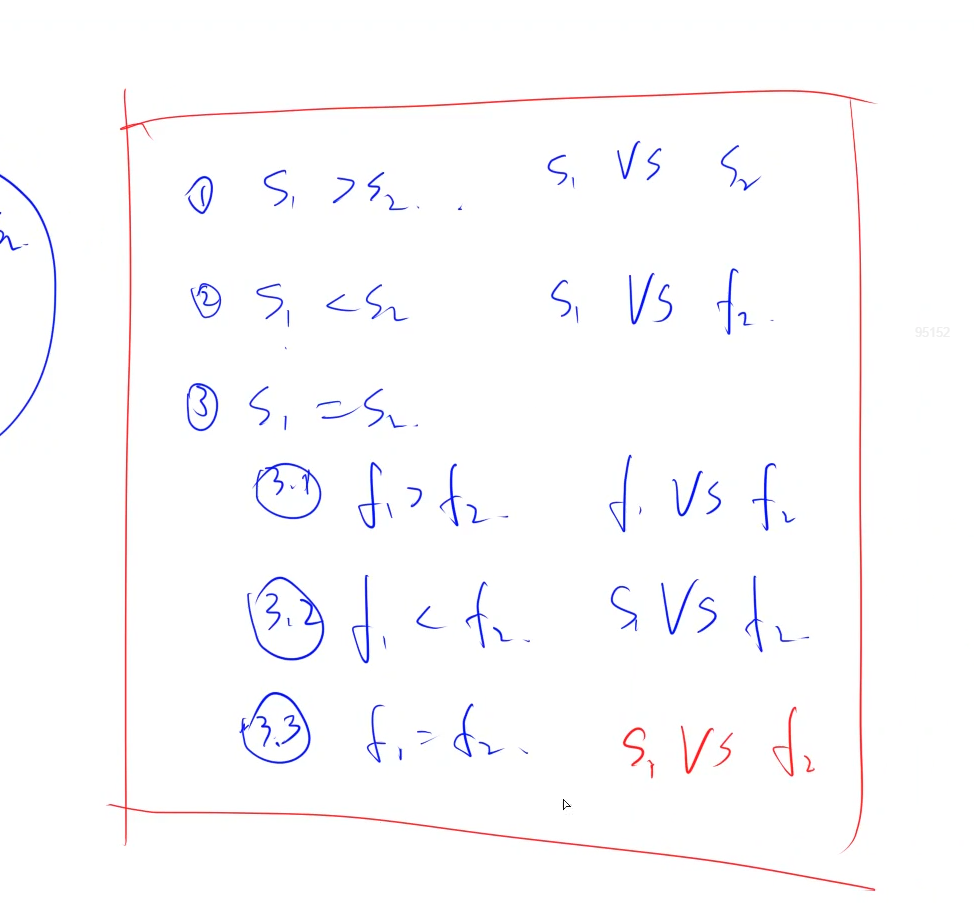
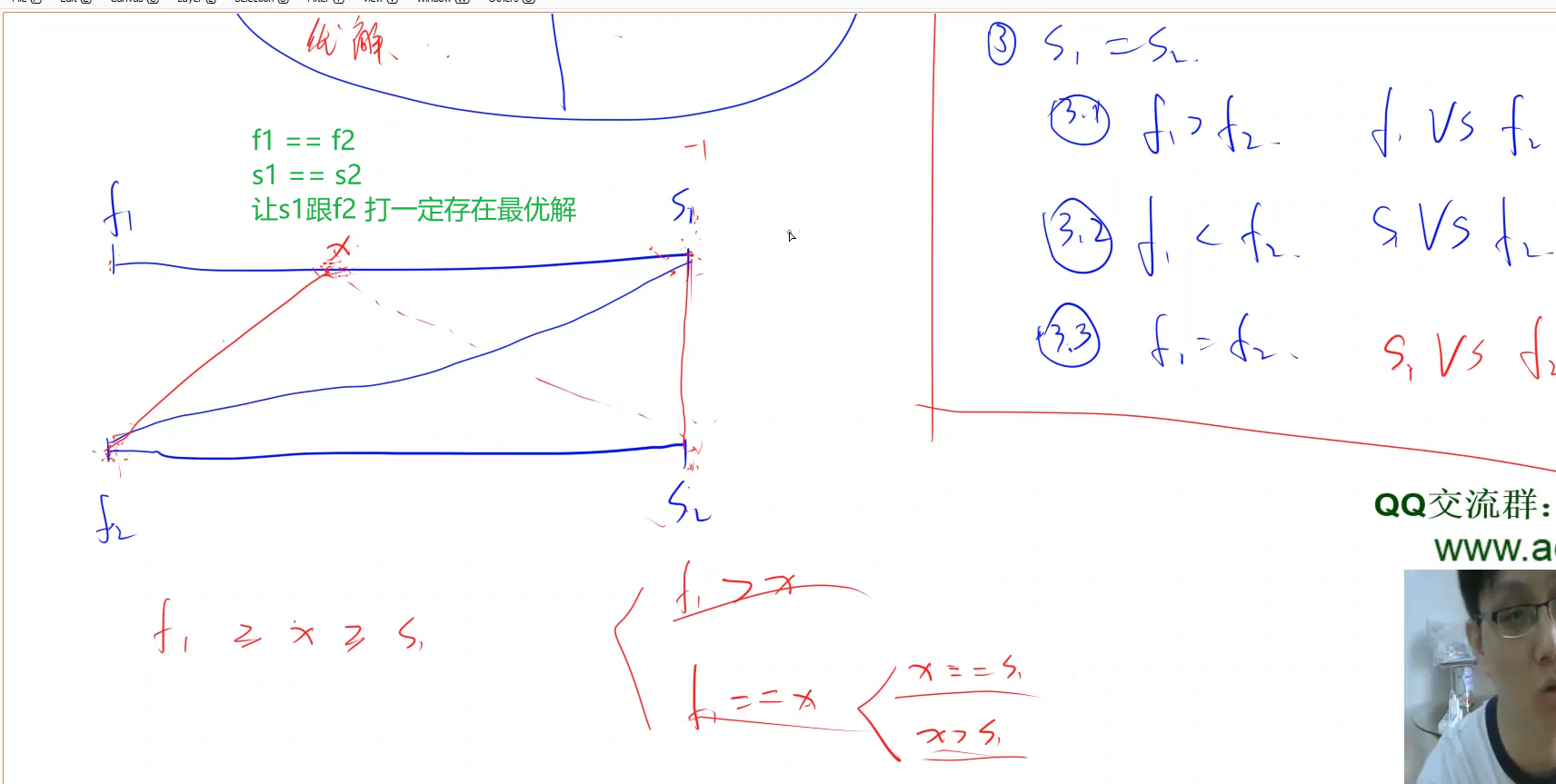
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int a[N], b[N];
int judge(int x, int y) {
    if (a[x] < b[y]) return -1;
    else if (a[x] > b[y]) return 1;
    else return 0;
}
int main() {
    int n;
    while (cin >> n, n) {
        for (int i = 1; i <= n; ++i) cin >> a[i];
        for (int i = 1; i <= n; ++i) cin >> b[i];
        //从大到小排序
        sort(a + 1, a + n + 1, greater<int>());
        sort(b + 1, b + n + 1, greater<int>());
        int f1 = 1, s1 = n, f2 = 1, s2 = n;
        int  res = 0;
        while (f1 <= s1) {
            //s1 < s2, 让s1跟f2比较
            if (judge(s1, s2) < 0) {
                res += judge(s1, f2);
                s1--, f2++;
            } else if (judge(s1, s2) > 0) { //s1 跟 s2比较
                res += judge(s1, s2);
                s1 --, s2 --;
            } else {    //s1 == s2
                if (judge(f1, f2) > 0) {    //f1 > f2 时 f1 跟 f2比较
                    res += judge(f1, f2);
                    f1 ++, f2 ++;
                } else {    //f1 <= f2都让s1 跟 f2比较
                    res += judge(s1, f2);
                    s1 --, f2 ++;
                }
            }
        }
        cout << res * 200 << endl;
    }
    return 0;
}