lc2103. 环和杆（位运算）

总计有 n 个环，环的颜色可以是红、绿、蓝中的一种。这些环分布穿在 10 根编号为 0 到 9 的杆上。

给你一个长度为 2n 的字符串 rings ，表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ，用于描述每个环：

第 i 对中的 第一个 字符表示第 i 个环的 颜色（’R’、’G’、’B’）。
第 i 对中的 第二个 字符表示第 i 个环的 位置，也就是位于哪根杆上（’0’ 到 ‘9’）。
例如，”R3G2B1” 表示：共有 n == 3 个环，红色的环在编号为 3 的杆上，绿色的环在编号为 2 的杆上，蓝色的环在编号为 1 的杆上。

找出所有集齐 全部三种颜色 环的杆，并返回这种杆的数量。

示例 1：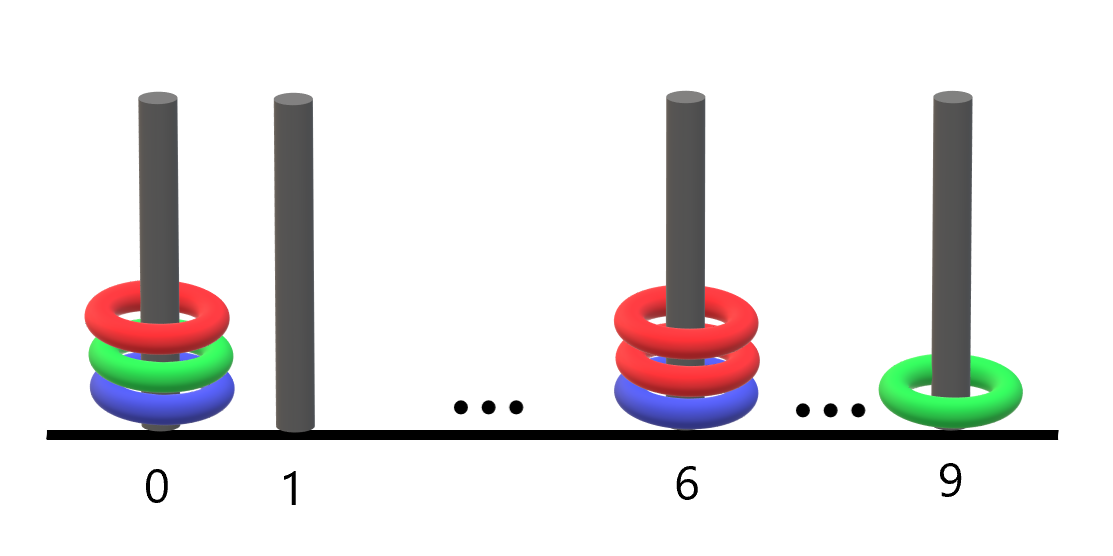

输入：rings = “B0B6G0R6R0R6G9”
输出：1
解释：

• 编号 0 的杆上有 3 个环，集齐全部颜色：红、绿、蓝。
• 编号 6 的杆上有 3 个环，但只有红、蓝两种颜色。
• 编号 9 的杆上只有 1 个绿色环。
  因此，集齐全部三种颜色环的杆的数目为 1 。
  示例 2：

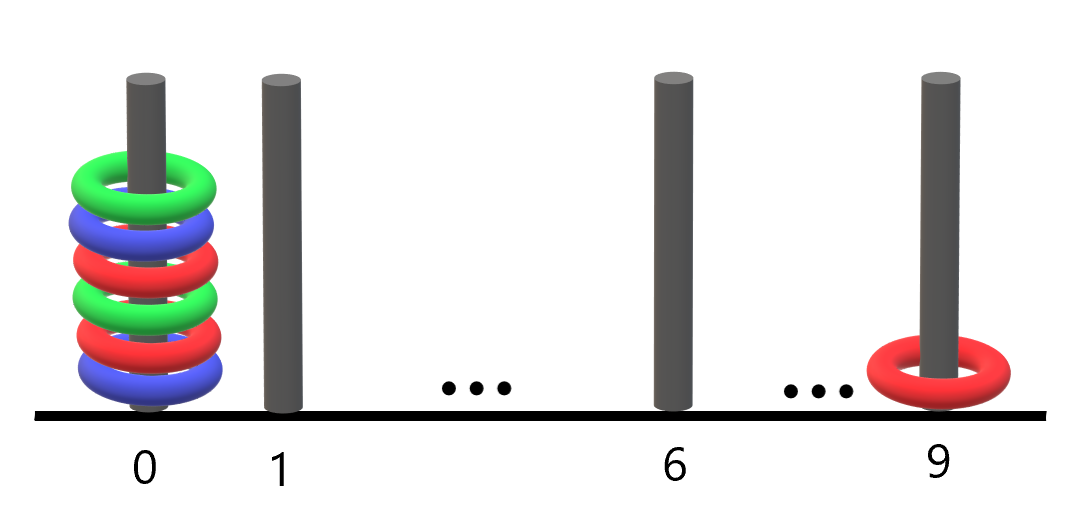
输入：rings = “B0R0G0R9R0B0G0”
输出：1
解释：

• 编号 0 的杆上有 6 个环，集齐全部颜色：红、绿、蓝。
• 编号 9 的杆上只有 1 个红色环。
  因此，集齐全部三种颜色环的杆的数目为 1 。
  示例 3：

输入：rings = “G4”
输出：0
解释：
只给了一个环，因此，不存在集齐全部三种颜色环的杆。

提示：

rings.length == 2 * n
1 <= n <= 100
如 i 是 偶数 ，则 rings[i] 的值可以取 ‘R’、’G’ 或 ‘B’（下标从 0 开始计数）
如 i 是 奇数 ，则 rings[i] 的值可以取 ‘0’ 到 ‘9’ 中的一个数字（下标从 0 开始计数）

class Solution {
    /**
    开一个长度10数组，当我们，遍历到B时就或上1，G或上2，R或上4
    如果结果数组为7说明都出现了，加入结果
     */
    public int countPoints(String rings) {
        char[] c = rings.toCharArray();
        int[] nums = new int[10];
        for (int i = 1; i < c.length; i += 2) {
            nums[c[i]-'0'] |= c[i-1] == 'B' ? 1 : c[i-1] == 'G'
            ? 2 : 4; 
        }
        int res = 0;
        for (int i = 0; i < 10; ++i) {
            if (nums[i] == 7) res++;
        }
        return res;
    }
}