存在一个 n x n 大小、下标从 0 开始的网格，网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组 artifacts ，artifacts 描述了矩形工件的位置，其中 artifacts[i] = [r1i, c1i, r2i, c2i] 表示第 i 个工件在子网格中的填埋情况：

    (r1i, c1i) 是第 i 个工件 左上 单元格的坐标，且
    (r2i, c2i) 是第 i 个工件 右下 单元格的坐标。
    你将会挖掘网格中的一些单元格，并清除其中的填埋物。如果单元格中埋着工件的一部分，那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来，你就可以提取该工件。

    给你一个下标从 0 开始的二维整数数组 dig ，其中 dig[i] = [ri, ci] 表示你将会挖掘单元格 (ri, ci) ，返回你可以提取的工件数目。

    生成的测试用例满足：

    不存在重叠的两个工件。
    每个工件最多只覆盖 4 个单元格。
    dig 中的元素互不相同。

    示例 1：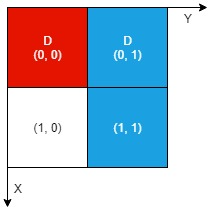
    image.png

    输入：n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
    输出：1
    解释：
    不同颜色表示不同的工件。挖掘的单元格用 ‘D’ 在网格中进行标记。
    有 1 个工件可以提取，即红色工件。
    蓝色工件在单元格 (1,1) 的部分尚未裸露出来，所以无法提取该工件。
    因此，返回 1 。
    示例 2：

    输入：n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
    输出：2
    解释：红色工件和蓝色工件的所有部分都裸露出来（用 ‘D’ 标记），都可以提取。因此，返回 2 。

    提示：

    1 <= n <= 1000
    1 <= artifacts.length, dig.length <= min(n2, 105)
    artifacts[i].length == 4
    dig[i].length == 2
    0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1
    r1i <= r2i
    c1i <= c2i
    不存在重叠的两个工件
    每个工件 最多 只覆盖 4 个单元格
    dig 中的元素互不相同

    1. class Solution {
    2.     public int digArtifacts(int n, int[][] artifacts, int[][] dig) {
    3.         int m = artifacts.length;
    4.         int[][] p = new int[n][n];   //点坐标
    5.         //先把暴露的点全部设置为-1
    6.         for (int[] t : dig) 
    7.             p[t[0]][t[1]] = -1;
    8.         int res = 0;
    9.         //遍历每个工件，如果有某个点不是-1，说明不能被挖出
    10.         for (int i = 0; i < m; ++i) {
    11.             int[] t = artifacts[i];
    12.             boolean flag = true;
    13.             for (int j = t[0]; j <= t[2]; ++j) 
    14.                 for (int k = t[1]; k <= t[3]; ++k)
    15.                     if (p[j][k] != -1) {
    16.                         flag = false;
    17.                         break;
    18.                     }
    19.             if (!flag) res++;
    20.         } 
    21.         return m - res;
    22.     }
    23. }