图 - lc2039. 网络空闲的时刻（建图 bfs） - 《算法》

给你一个有 n 个服务器的计算机网络，服务器编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示服务器 ui 和 vi 之间有一条信息线路，在一秒内它们之间可以传输任意数目的信息。再给你一个长度为 n 且下标从 0 开始的整数数组 patience 。

题目保证所有服务器都是相通的，也就是说一个信息从任意服务器出发，都可以通过这些信息线路直接或间接地到达任何其他服务器。

编号为 0 的服务器是主服务器，其他服务器为数据服务器。每个数据服务器都要向主服务器发送信息，并等待回复。信息在服务器之间按最优线路传输，也就是说每个信息都会以最少时间到达主服务器。主服务器会处理所有新到达的信息并立即按照每条信息来时的路线反方向发送回复信息。

在 0 秒的开始，所有数据服务器都会发送各自需要处理的信息。从第 1 秒开始，每一秒最开始时，每个数据服务器都会检查它是否收到了主服务器的回复信息（包括新发出信息的回复信息）：

如果还没收到任何回复信息，那么该服务器会周期性重发信息。数据服务器 i 每 patience[i] 秒都会重发一条信息，也就是说，数据服务器 i 在上一次发送信息给主服务器后的 patience[i] 秒后会重发一条信息给主服务器。
否则，该数据服务器不会重发信息。
当没有任何信息在线路上传输或者到达某服务器时，该计算机网络变为空闲状态。

请返回计算机网络变为空闲状态的最早秒数。

示例 1：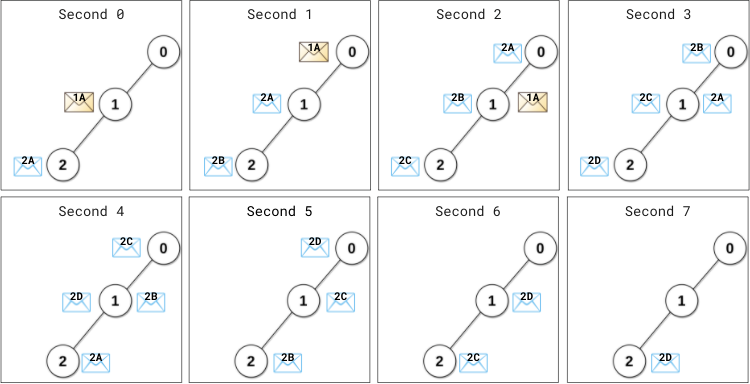

输入：edges = [[0,1],[1,2]], patience = [0,2,1]
输出：8
解释：
0 秒最开始时，

数据服务器 1 给主服务器发出信息（用 1A 表示）。
数据服务器 2 给主服务器发出信息（用 2A 表示）。

1 秒时，

信息 1A 到达主服务器，主服务器立刻处理信息 1A 并发出 1A 的回复信息。
数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒（1 < patience[1] = 2），所以不会重发信息。
数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒（1 == patience[2] = 1），所以它重发一条信息（用 2B 表示）。

2 秒时，

回复信息 1A 到达服务器 1 ，服务器 1 不会再重发信息。
信息 2A 到达主服务器，主服务器立刻处理信息 2A 并发出 2A 的回复信息。
服务器 2 重发一条信息（用 2C 表示）。
…
4 秒时，
回复信息 2A 到达服务器 2 ，服务器 2 不会再重发信息。
…
7 秒时，回复信息 2D 到达服务器 2 。

从第 8 秒开始，不再有任何信息在服务器之间传输，也不再有信息到达服务器。
所以第 8 秒是网络变空闲的最早时刻。
示例 2：

输入：edges = [[0,1],[0,2],[1,2]], patience = [0,10,10]
输出：3
解释：数据服务器 1 和 2 第 2 秒初收到回复信息。
从第 3 秒开始，网络变空闲。

提示：

n == patience.length
2 <= n <= 105
patience[0] == 0
对于 1 <= i < n ，满足 1 <= patience[i] <= 105
1 <= edges.length <= min(105, n * (n - 1) / 2)
edges[i].length == 2
0 <= ui, vi < n
ui != vi
不会有重边。
每个服务器都直接或间接与别的服务器相连。

class Solution {
    //建无向图，然后先求dist[i]即每个点到0的距离,然后求每个点的最晚发送时间，维护最大时间即可
    static int N = 100010, M = N * 2, INF = 0x3f3f3f3f;
    static int[] h = new int[N], e = new int[M], ne = new int[M];
    static int[] dist = new int[N];
    int idx;
    void add(int a, int b) {
        e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
    }
    public int networkBecomesIdle(int[][] edges, int[] patience) {
        Arrays.fill(h, -1);
        Arrays.fill(dist, INF);
        //建图
        for (int[] t : edges) {
            add(t[0], t[1]);
            add(t[1], t[0]);
        }
        Deque<Integer> q = new LinkedList<>();
        q.addLast(0);
        dist[0] = 0;
        while (!q.isEmpty()) {
            int t = q.pollFirst();
            for (int i = h[t]; i != -1; i = ne[i]) {
                int j = e[i];
                if (dist[j] != INF) continue;
                dist[j] = dist[t] + 1;
                q.addLast(j);
            }
        }
        int res = 0;
        for (int i = 0; i < patience.length; ++i) {
            int di = dist[i] * 2, d = patience[i];
            //如果d比di大，直接返回di, 否则最后一次发送时间为 (di - 1) / d * d,其(di - 1) / d 为发送次数 
            int cur = d >= di ? di : (di - 1) / d * d + di;
            res = Math.max(res, cur); 
        }
        //下一秒空闲
        return res + 1;
    }
}