acwing320.能量项链

在 Mars 星球上，每个 Mars 人都随身佩带着一串能量项链，在项链上有 NN 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。
并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样，通过吸盘（吸盘是 Mars 人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 mm，尾标记为 rr，后一颗能量珠的头标记为 rr，尾标记为 nn，则聚合后释放的能量为 m×r×nm×r×n（Mars 单位），新产生的珠子的头标记为 mm，尾标记为 nn。
需要时，Mars 人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。
显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。
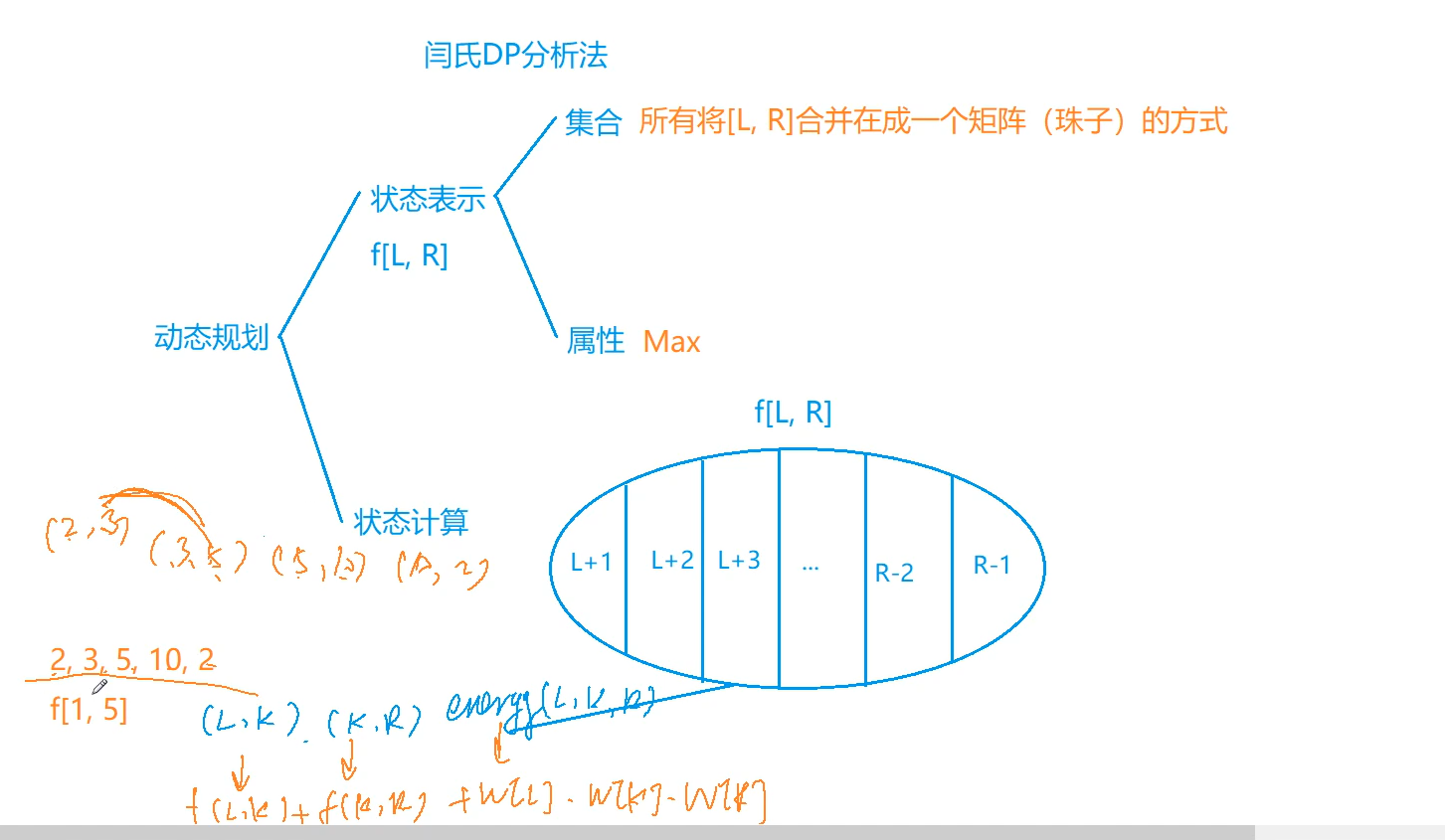
例如：设 N=4N=4，44 颗珠子的头标记与尾标记依次为 (2，3)(3，5)(5，10)(10，2)(2，3)(3，5)(5，10)(10，2)。
我们用记号 ⊕⊕ 表示两颗珠子的聚合操作，(j⊕k)(j⊕k) 表示第 jj，kk 两颗珠子聚合后所释放的能量。则
第 4、14、1 两颗珠子聚合后释放的能量为：(4⊕1)=10×2×3=60(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。

输入格式

输入的第一行是一个正整数 NN，表示项链上珠子的个数。
第二行是 NN 个用空格隔开的正整数，所有的数均不超过 10001000，第 ii 个数为第 ii 颗珠子的头标记，当 i至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

输出格式

输出只有一行，是一个正整数 EE，为一个最优聚合顺序所释放的总能量。

数据范围

4≤N≤1004≤N≤100,
1≤E≤2.1×1091≤E≤2.1×109

输入样例：

4 2 3 5 10

输出样例：

710

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210;
int f[N][N];
int w[N];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> w[i];
        w[i+n] = w[i];
    }
    //dp
    for (int len = 3; len <= n + 1; ++len) 
        for (int l = 1; len + l -1 <= 2 * n; ++ l) {
            int r = len + l - 1;
            for (int k = l+1; k < r; ++k) 
                f[l][r] = max(f[l][r],f[l][k] + f[k][r] + w[l]*w[r]*w[k]);
        }
    int res = 0;
    for (int i = 1; i <= n; ++i) {
        res = max(res,f[i][i+n]);
    }
    cout << res;
    return 0;
}