你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的。如果网格上只有陆地或者海洋，请返回 -1。

    我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

    示例 1：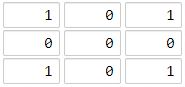
    image.png

    输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
    输出：2
    解释：
    海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。
    示例 2：

    输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
    输出：4
    解释：
    海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

    提示：

    n == grid.length
    n == grid[i].length
    1 <= n <= 100
    grid[i][j] 不是 0 就是 1

    1. class Solution {
    2.     static private int[] dx = {-1,0,1,0}, dy = {0,1,0,-1};
    3.     public int maxDistance(int[][] grid) {
    4.         int n = grid.length;
    5.         //dist记录步数
    6.         int[][] dist = new int[n][n];
    7.         //初始化可以起到判重 保证每个点只入队一次
    8.         for (int i = 0; i < n; ++i) 
    9.             for (int j = 0; j < n; ++j) dist[i][j] = -1;
    10.         Deque<int[]> q = new ArrayDeque<>();
    11.         for (int i = 0; i < n; ++i) 
    12.             for (int j = 0; j < n; ++j) {
    13.                 if (grid[i][j] == 1) {
    14.                     q.addLast(new int[]{i,j});
    15.                     dist[i][j] = 0;
    16.                 } 
    17.             }
    18.         //全是陆地或者海洋直接返回
    19.         if (q.size() == n*n || q.size() == 0) return -1;
    20.         int res = 0;
    21.         while (!q.isEmpty()) {
    22.             int[] t = q.pollFirst();
    23.             for (int i = 0; i < 4; ++i) {
    24.                 int a = dx[i] + t[0], b = dy[i] + t[1];
    25.                 if (a < 0 || a >= n || b < 0 || b >= n) continue;
    26.                 if (dist[a][b] != -1) continue;
    27.                 dist[a][b] = dist[t[0]][t[1]] + 1;
    28.                 q.addLast(new int[]{a,b});
    29.                 //更新
    30.                 res = Math.max(res,dist[a][b]);
    31.             }
    32.         }
    33.         return res;
    34.     }
    35. }
    1. class Solution {
    2.     static int[] dirs = new int[]{-1, 0, 1, 0, -1};
    3.     public int maxDistance(int[][] grid) {
    4.         int n = grid.length, m = grid[0].length;
    5.         Deque<int[]> q = new LinkedList<>();
    6.         for (int i = 0; i < n; ++i) 
    7.             for (int j = 0; j < m; ++j) 
    8.                 if (grid[i][j] == 1) q.addLast(new int[]{i, j});
    9.         //全是陆地，或者海洋
    10.         if (q.size() == n * m || q.size() == 0) return -1;
    11.         while (!q.isEmpty()) {
    12.             int[] t = q.pollFirst();
    13.             for (int i = 0; i < 4; ++i) {
    14.                 int x = t[0] + dirs[i], y = t[1] + dirs[i + 1];
    15.                 if (x < 0 || x >= n || y < 0 || y >= m) continue;
    16.                 if (grid[x][y] != 0) continue;
    17.                 grid[x][y] = grid[t[0]][t[1]] + 1;
    18.                 q.addLast(new int[]{x, y});
    19.             }
    20.         }
    21.         int res = 0;
    22.         for (int i = 0; i < n; ++i) 
    23.             for (int j = 0; j < m; ++j) 
    24.                 res = Math.max(res, grid[i][j]);
    25.         return res - 1;
    26.     }
    27. }