给你一座由 n x n 个街区组成的城市，每个街区都包含一座立方体建筑。给你一个下标从 0 开始的 n x n 整数矩阵 grid ，其中 grid[r][c] 表示坐落于 r 行 c 列的建筑物的 高度 。

    城市的 天际线 是从远处观察城市时，所有建筑物形成的外部轮廓。从东、南、西、北四个主要方向观测到的 天际线 可能不同。

    我们被允许为 任意数量的建筑物 的高度增加 任意增量（不同建筑物的增量可能不同） 。 高度为 0 的建筑物的高度也可以增加。然而，增加的建筑物高度 不能影响 从任何主要方向观察城市得到的 天际线 。

    在 不改变 从任何主要方向观测到的城市 天际线 的前提下，返回建筑物可以增加的 最大高度增量总和 。

    示例 1：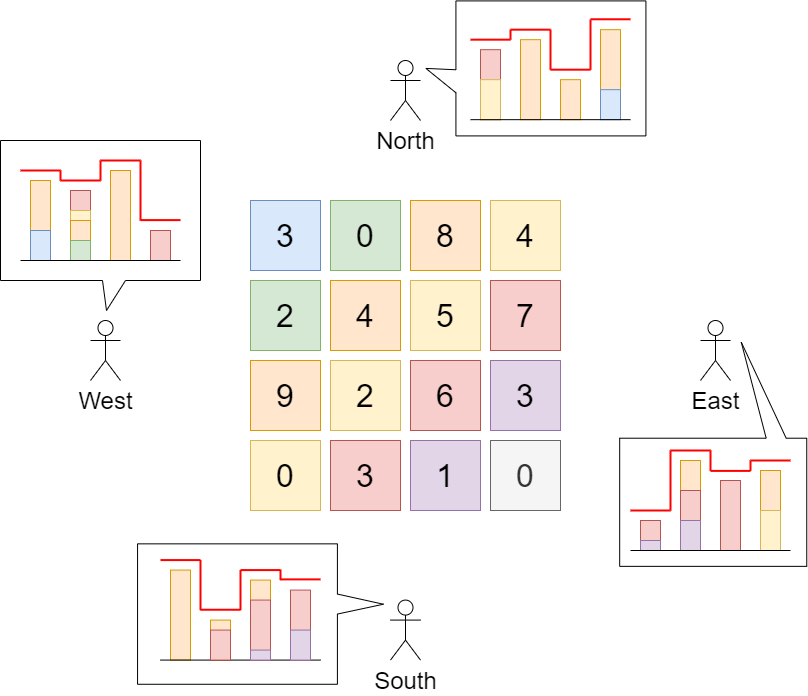
    image.png

    输入：grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
    输出：35
    解释：建筑物的高度如上图中心所示。
    用红色绘制从不同方向观看得到的天际线。
    在不影响天际线的情况下，增加建筑物的高度：
    gridNew = [ [8, 4, 8, 7],
    [7, 4, 7, 7],
    [9, 4, 8, 7],
    [3, 3, 3, 3] ]
    示例 2：

    输入：grid = [[0,0,0],[0,0,0],[0,0,0]]
    输出：0
    解释：增加任何建筑物的高度都会导致天际线的变化。

    提示：

    n == grid.length
    n == grid[r].length
    2 <= n <= 50
    0 <= grid[r][c] <= 100

    1. class Solution {
    2.     public int maxIncreaseKeepingSkyline(int[][] grid) {
    3.         int n = grid.length, m = grid[0].length;
    4.         int[] r = new int[n];
    5.         int[] c = new int[m];
    6.         //获得每行每列最大值
    7.         for(int i = 0; i < n; ++i)
    8.             for(int j = 0; j < m; ++j){
    9.                 r[i] = Math.max(r[i],grid[i][j]);
    10.                 c[j] = Math.max(c[j],grid[i][j]);
    11.             }
    12.         int res = 0;
    13.         for(int i = 0; i < n; ++i)
    14.             for(int j = 0; j < m; ++j){
    15.                 int t = Math.min(r[i],c[j]);
    16.                 //如果比行列的最大值小，说明能填充
    17.                 if(grid[i][j] < t)
    18.                     res += t - grid[i][j];
    19.             }
    20.         return res;
    21.     }
    22. }