lc2049. 统计最高分的节点数目（图论 dfs）

给你一棵根节点为 0 的 二叉树 ，它总共有 n 个节点，节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树，其中 parents[i] 是节点 i 的父节点。由于节点 0 是根，所以 parents[0] == -1 。

一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是，将这个节点和与它相连的边全部 删除 ，剩余部分是若干个 非空 子树，这个节点的 分数 为所有这些子树 大小的乘积 。

请你返回有 最高得分 节点的 数目 。

示例 1: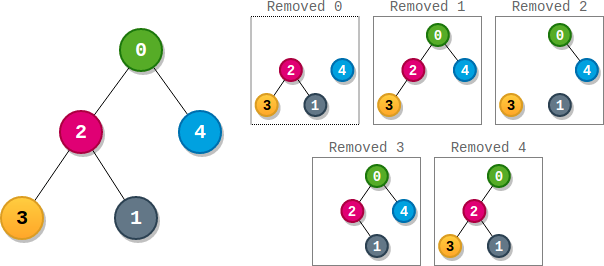

输入：parents = [-1,2,0,2,0]
输出：3
解释：
- 节点 0 的分数为：3 1 = 3
- 节点 1 的分数为：4 = 4
- 节点 2 的分数为：1 1 * 2 = 2
- 节点 3 的分数为：4 = 4
- 节点 4 的分数为：4 = 4
最高得分为 4 ，有三个节点得分为 4 （分别是节点 1，3 和 4 ）。
示例 2：

输入：parents = [-1,2,0]
输出：2
解释：
- 节点 0 的分数为：2 = 2
- 节点 1 的分数为：2 = 2
- 节点 2 的分数为：1 * 1 = 1
最高分数为 2 ，有两个节点分数为 2 （分别为节点 0 和 1 ）。

提示：

n == parents.length
2 <= n <= 105
parents[0] == -1
对于 i != 0 ，有 0 <= parents[i] <= n - 1
parents 表示一棵二叉树。

class Solution {
    static int N = 100010, M = N * 2;
    static int[] h = new int[N], e = new int[M], ne = new int[M];
    static int[] f = new int[N];    //存储以该节点为根节点的子树有多少个节点
    int idx;
    //建图
    private void add(int a, int b) {
        e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
    }
    public int countHighestScoreNodes(int[] parents) {
        Arrays.fill(h, -1);
        int n = parents.length;
        for (int i = 1; i < n; ++i) 
            add(parents[i], i);
        dfs(0);
        long maxi = 0;
        int res = 0;
        for (int i = 0; i < n; ++i) {
            long cur = 1;
            for (int j = h[i]; j != -1; j = ne[j]) cur *= f[e[j]];
            //判断是不是根节点
            if (i != 0) cur *= (n - f[i]);
            if (cur > maxi) {
                maxi = cur; 
                res = 1;
            } else if (cur == maxi) res++;
        }
        return res;
    }
    //统计每个节点子树有多少个节点
    int dfs(int u) {
        int res = 1;
        for (int i = h[u]; i != -1; i = ne[i]) res += dfs(e[i]);
        f[u] = res;
        return res;
    }
}