每当下雨时，农夫约翰的田地总是被洪水淹没。
由于田地不是完全水平的，所以一些地方充满水后，留下了许多被水隔开的“岛”。
约翰的田地被描述为由 NN 个连续高度值 H1,…,HNH1,…,HN 指定的一维场景。
假设该场景被无限高的围墙包围着，请考虑暴雨期间发生的情况：
最低处首先被水覆盖，形成一些不连贯的岛，随着水位的不断上升，这些岛最终都会被覆盖。
一旦水位等于一块田地的高度，那块田地就被认为位于水下。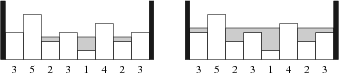
image.png
上图显示了一个示例：在左图中，我们只加入了刚好超过 11 单位的水，此时剩下 44 个岛（最大岛屿剩余数量），而在右图中，我们共加入了 77 单位的水，此时仅剩下 22 个岛。
请计算，暴风雨期间我们能在某个时间点看到的最大岛屿数量。
水会一直上升到所有田地都在水下。

输入格式

第一行包含整数 NN。
接下来 NN 行，每行包含一个整数表示 HiHi。

输出格式

输出暴风雨期间我们能在某个时间点看到的最大岛屿数量。

数据范围

1≤N≤1051≤N≤105,
1≤Hi≤1091≤Hi≤109

输入样例：

8 3 5 2 3 1 4 2 3

输出样例：

4
image.png

  1. //先去掉左右重复的,然后按照高低排序,然后遍历,分情况讨论
  2. #include <iostream>
  3. #include <cstring>
  4. #include <algorithm>
  6. using namespace std;
  8. #define x first
  9. #define y second
  11. typedef pair<int,int> PII;
  13. const int N = 100010;
  15. PII q[N];
  16. int h[N];
  17. int n;
  19. int main() {
  20.     cin >> n;
  21.     for (int i = 1; i <= n; ++i) scanf("%d",&h[i]);
  23.     n = unique(h + 1, h + n + 1) - h - 1;   // 相邻判重
  24.     h[n+1] = 0;     // 后续代码可能会用到第n + 1个位置，需要把第n + 1个位置清空
  25.     for (int i = 1; i <= n; ++i) q[i] = {h[i],i};
  27.     sort(q+1, q+n+1);
  29.     int res = 1, cnt = 1;
  30.     for (int i = 1; i <= n; ++i) {
  31.         int k = q[i].y;
  32.         if (h[k-1] < h[k] && h[k+1] < h[k]) cnt--;
  33.         else if (h[k-1] > h[k] && h[k+1] > h[k]) cnt++;
  35.         if (q[i].x != q[i+1].x)     //当有两个高度相等时,必须先将同一高度统计完再记录答案 
  36.             res = max(res,cnt);
  37.     }
  39.     cout << res << endl;
  40.     return 0;
  41. }