lc802. 找到最终的安全状态（反向图 拓扑排序）

在有向图中，以某个节点为起始节点，从该点出发，每一步沿着图中的一条有向边行走。如果到达的节点是终点（即它没有连出的有向边），则停止。

对于一个起始节点，如果从该节点出发，无论每一步选择沿哪条有向边行走，最后必然在有限步内到达终点，则将该起始节点称作是 安全 的。

返回一个由图中所有安全的起始节点组成的数组作为答案。答案数组中的元素应当按 升序 排列。

该有向图有 n 个节点，按 0 到 n - 1 编号，其中 n 是 graph 的节点数。图以下述形式给出：graph[i] 是编号 j 节点的一个列表，满足 (i, j) 是图的一条有向边。

示例 1：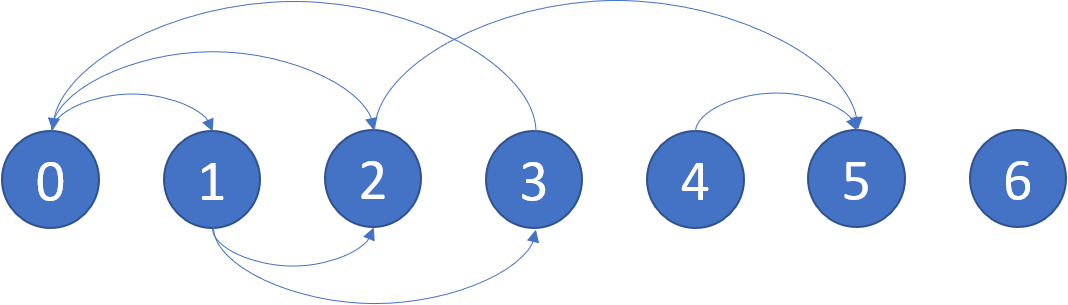

输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]
解释：示意图如上。
示例 2：

输入：graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出：[4]

提示：

n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
graph[i] 按严格递增顺序排列。
图中可能包含自环。
图中边的数目在范围 [1, 4 * 104] 内。

class Solution {
    /**
     */
    int N = (int)1e4+10, M = 4 * N;
    int idx;
    int[] h = new int[N], e = new int[M], ne = new int[M];
    int[] cnts = new int[N];
    //邻接表存储
    public void add(int x, int y){
        e[idx] = y; ne[idx] = h[x]; h[x] = idx++; 
    }
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int n = graph.length;
        //存反向图，并统计入度
        Arrays.fill(h,-1);
        for(int i = 0; i < n; ++i){
            for(int j : graph[i]){
                add(j,i);
                cnts[i]++;
            }
        }
        //BFS 求反向图拓扑排序
        Deque<Integer> q = new ArrayDeque<>();
        for(int i = 0; i < n; ++i){
            if(cnts[i] == 0) q.addLast(i);
        }
        while(!q.isEmpty()){
            int x = q.pollFirst();
            for(int i = h[x]; i != -1; i = ne[i]){
                int j = e[i];
                if(--cnts[j] == 0) q.addLast(j); 
            }
        }
        List<Integer> res = new ArrayList<>();
        for(int i = 0; i < n; ++i){
            if(cnts[i] == 0) res.add(i);
        }
        return res;
    }
}