给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

    提醒一下，二叉搜索树满足下列约束条件：

    节点的左子树仅包含键 小于 节点键的节点。
    节点的右子树仅包含键 大于 节点键的节点。
    左右子树也必须是二叉搜索树。

    示例 1：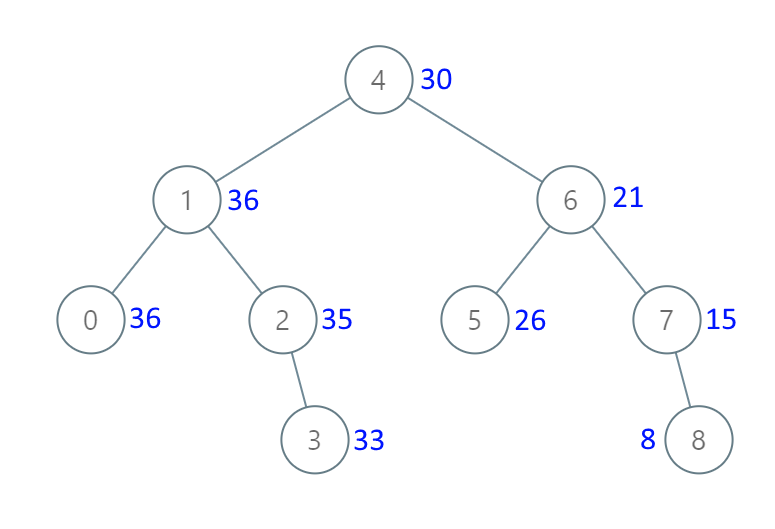
    image.png

    输入：root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
    输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
    示例 2：

    输入：root = [0,null,1]
    输出：[1,null,1]
    示例 3：

    输入：root = [1,0,2]
    输出：[3,3,2]
    示例 4：

    输入：root = [3,2,4,1]
    输出：[7,9,4,10]

    提示：

    树中的节点数介于 0 和 104 之间。
    每个节点的值介于 -104 和 104 之间。
    树中的所有值 互不相同 。
    给定的树为二叉搜索树。

    1. class Solution {
    2.     public TreeNode convertBST(TreeNode root) {
    3.         long sum = 0;
    4.         TreeNode tem = root;
    5.         //求节点和
    6.         sum = dfs(tem);
    7.         TreeNode cur = root;
    8.         Deque<TreeNode> stack = new LinkedList<>();
    9.         //val表示当前节点中序遍历之前的和
    10.         long val = 0;
    11.         while (cur != null || !stack.isEmpty()) {
    12.             if (cur != null) {
    13.                 stack.push(cur);
    14.                 cur = cur.left;
    15.             } else {
    16.                 TreeNode node = stack.poll();
    17.                 int t = node.val;
    18.                 node.val = (int)(sum - val);
    19.                 val += t;
    20.                 cur = node.right;
    21.             }
    22.         }
    23.         return root;
    24.     }
    25.     public long dfs(TreeNode root) {
    26.         if (root == null) return 0;
    27.         long sum = root.val;
    28.         sum += dfs(root.left);
    29.         sum += dfs(root.right);
    30.         return sum;
    31.     }
    32. }