Copy of lc1020. 飞地的数量（并查集&DFS 多源BFS）

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：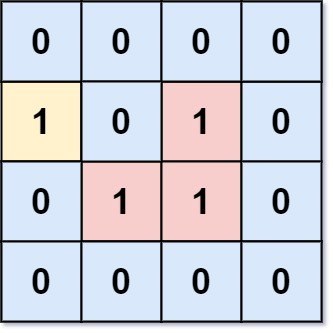

输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。
示例 2：

输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] 的值为 0 或 1

多源bfs

class Solution {
    /**
    将所有「边缘陆地」看做与超级源点相连，起始将所有「边缘陆地」进行入队（等价于只将超级源点入队，然后取出超级源点并进行拓展）。
然后是常规的 BFS 过程，所有能够出队/入队的陆地格子，都代表与「边缘陆地」联通，都不属于「飞地」，对其进行标记。
最后遍历整个棋盘，统计所有未被标记的「陆地」格子数量即是答案。
    */
    static int[] dirs = new int[]{-1,0,1,0,-1};
    public int numEnclaves(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        Deque<int[]> q = new ArrayDeque<>();
        int res = 0;
        for (int i = 0; i < n; ++i) 
            for (int j = 0; j < m; ++j) 
                if ((i == 0 || i == n-1 || j == 0 || j == m-1) && grid[i][j] == 1) {
                    q.addLast(new int[]{i,j});
                    while (!q.isEmpty()) {
                        int[] t = q.pollFirst();
                        int x = t[0], y = t[1];
                        grid[x][y] = 0;
                        for (int k = 0; k < 4; ++k) {
                            int a = x + dirs[k], b = y + dirs[k+1];
                            if (a < 0 || a >= n || b < 0 || b >= m) 
                                continue;
                            if (grid[a][b] == 1) q.addLast(new int[]{a,b});
                        }
                    }
                }
        for (int i = 0; i < n; ++i) 
            for (int j = 0; j < m; ++j) 
                if (grid[i][j] == 1) res++;
        return res;
    }
}