lc85. 最大矩形（单调栈）

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：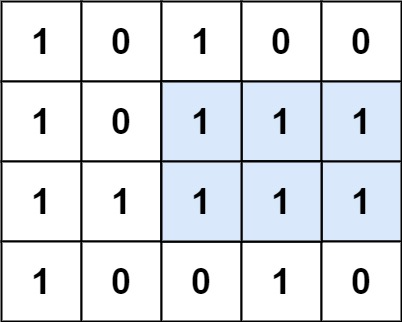

输入：matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]
输出：6
解释：最大矩形如上图所示。
示例 2：

输入：matrix = []
输出：0
示例 3：

输入：matrix = [[“0”]]
输出：0
示例 4：

输入：matrix = [[“1”]]
输出：1
示例 5：

输入：matrix = [[“0”,”0”]]
输出：0

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 ‘0’ 或 ‘1’

class Solution {
    /**
    我们可以将此题转化为上道直方图求矩形最大面积，怎么转化？
    遍历每一行，只有当当前位置是'1'时，我们才把它以前的值加上，
    例如"1101","1011" 第二行我们可以转化为"2002"
    然后对每一行运用单调栈求解每一行最大值，并维护答案
     */
    int[] st;   //模拟栈
    int tt;     //模拟栈顶
    public int maximalRectangle(char[][] matrix) {
        int n = matrix.length, m = n == 0 ? 0 : matrix[0].length;
        if (n == 0) return 0;
        int res = 0;
        st = new int[m+1];
        //每行多开两个是因为后面我们加入两个哨兵，因为我们维护的是单调上升栈
        int[][] dir = new int[n][m+2]; 
        for (int i = 0; i < n; ++i) 
            for (int j = 1; j <= m; ++j) {
                dir[i][j] = matrix[i][j-1]-'0';
                //只有当当前值是"1"才加上之前的值
                if (i > 0 && matrix[i][j-1] == '1')
                    dir[i][j] += dir[i-1][j];
            }
        //求解每一行的最大值
        for (int i = 0; i < n; ++i) {
            tt = 0;
            int[] c = dir[i];
            c[0] = 0;
            c[m+1] = 0;
            for (int j = 1; j <= m+1; ++j) {
                while (tt > 0 && c[st[tt]] >= c[j]) {
                    int cur = c[st[tt--]];
                    int l = st[tt]+1;
                    int r = j-1;
                    res = Math.max(res,cur*(r-l+1));
                }
                st[++tt] = j;
            }
        }
        return res;
    }
}