lc1765. 地图中的最高点（多源bfs）

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。
如果一个格子是是 水域 ，那么它的高度必须为 0 。
任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）
找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：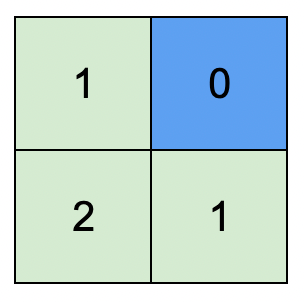

输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。
示例 2：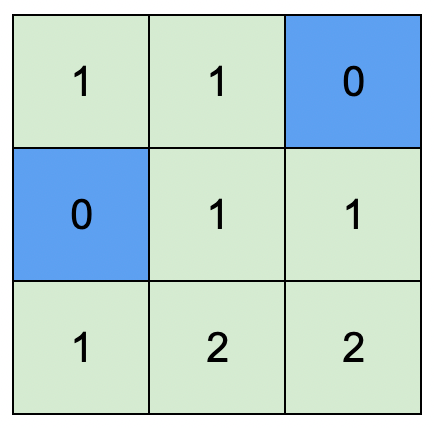

输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

提示：

m == isWater.length
n == isWater[i].length
1 <= m, n <= 1000
isWater[i][j] 要么是 0 ，要么是 1 。
至少有 1 个水域格子。

class Solution {
    private static int[] dx = {0,1,0,-1}, dy = {1,0,-1,0}; 
    public int[][] highestPeak(int[][] isWater) {
        int n = isWater.length, m = isWater[0].length;
        boolean[][] st = new boolean[n][m];
        Deque<int[]> q = new ArrayDeque<>();
        for (int i = 0; i < n; ++i) 
            for (int j = 0; j < m; ++j) {
                if (isWater[i][j] == 1) {
                    q.addLast(new int[]{i,j});
                    st[i][j] = true;
                    isWater[i][j] = 0;
                }
            }  
        while (!q.isEmpty()) {
            int[] t = q.pollFirst();
            for (int i = 0; i < 4; ++i) {
                int a = t[0] + dx[i], b = t[1] + dy[i];
                if (a < 0 || a >= n || b < 0 || b >= m) continue;
                if (st[a][b]) continue;
                st[a][b] = true;
                isWater[a][b] = isWater[t[0]][t[1]] + 1;
                q.addLast(new int[]{a,b});
            }
        }
        return isWater;
    }
}