有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回 网格坐标 result 的 2D列表 ，其中 result[i] = [ri, ci] 表示雨水可以从单元格 (ri, ci) 流向 太平洋和大西洋 。

示例 1：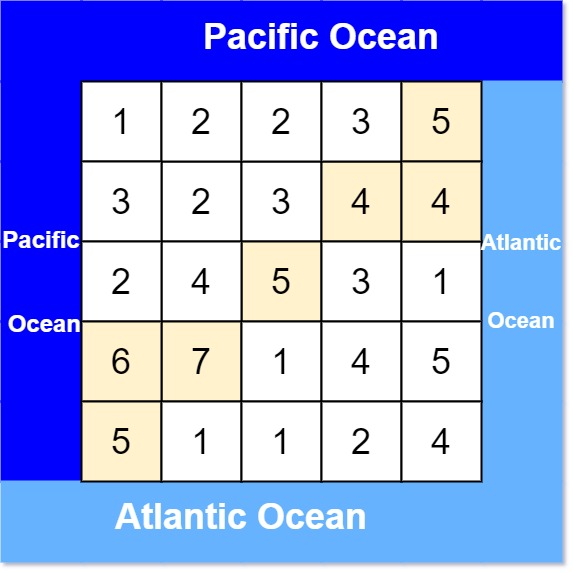
image.png

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 105

  1. class Solution {
  2.     /**
  3.     分别从左，上边界来标记能到哪，再从右，下边界来标记能到哪，求都能到的地方
  4.      */
  5.     public List<List<Integer>> pacificAtlantic(int[][] heights) {
  6.         int n = heights.length, m = heights[0].length;
  7.         boolean[][] st1 = new boolean[n][m], st2 = new boolean[n][m];
  8.         List<List<Integer>> res = new ArrayList<>();
  9.         Deque<int[]> q = new LinkedList<>();
  10.         int[] dirs = new int[]{-1, 0, 1, 0, -1};
  11.         for (int i = 0; i < n; ++i) {
  12.             q.addLast(new int[]{i, 0});
  13.             st1[i][0] = true;
  14.         }
  15.         for (int i = 0; i < m; ++i) {
  16.             q.addLast(new int[]{0, i});
  17.             st1[0][i] = true;
  18.         }
  19.         while (!q.isEmpty()) {
  20.             int[] t = q.pollLast();
  21.             for (int i = 0; i < 4; ++i) {
  22.                 int x = t[0] + dirs[i], y = t[1] + dirs[i + 1];
  23.                 if (x < 0 || x >= n || y < 0 || y >= m) continue;
  24.                 if (st1[x][y]) continue;
  25.                 if (heights[x][y] >= heights[t[0]][t[1]]) {
  26.                     q.addLast(new int[]{x, y});
  27.                     st1[x][y] = true;
  28.                 }
  29.             }
  30.         }
  31.         for (int i = 0; i < n; ++i) {
  32.             q.addLast(new int[]{i, m - 1});
  33.             st2[i][m - 1] = true;
  34.         }
  35.         for (int i = 0; i < m; ++i) {
  36.             q.addLast(new int[]{n - 1, i});
  37.             st2[n - 1][i] = true;
  38.         }
  39.         while (!q.isEmpty()) {
  40.             int[] t = q.pollLast();
  41.             for (int i = 0; i < 4; ++i) {
  42.                 int x = t[0] + dirs[i], y = t[1] + dirs[i + 1];
  43.                 if (x < 0 || x >= n || y < 0 || y >= m) continue;
  44.                 if (st2[x][y]) continue;
  45.                 if (heights[x][y] >= heights[t[0]][t[1]]) {
  46.                     q.addLast(new int[]{x, y});
  47.                     st2[x][y] = true;
  48.                 }
  49.             }
  50.         }
  51.         for (int i = 0; i < n; ++i) 
  52.             for (int j = 0; j < m; ++j) 
  53.                 if (st1[i][j] && st2[i][j]) {
  54.                     List<Integer> list = new ArrayList<>();
  55.                     list.add(i);
  56.                     list.add(j);
  57.                     res.add(new ArrayList<>(list));
  58.                 }
  59.         return res;
  60.     }
  61. }

dfs

  1. class Solution {
  2.     /**
  3.     dfs
  4.      */
  5.     int[][] h;
  6.     boolean[][] st1, st2;
  7.     int n, m;
  8.     int[] dirs = new int[]{-1, 0, 1, 0, -1};
  9.     public List<List<Integer>> pacificAtlantic(int[][] heights) {
  10.         h = heights;
  11.         n = heights.length; m = heights[0].length;
  12.         st1 = new boolean[n][m]; st2 = new boolean[n][m];
  13.         for (int i = 0; i < n; ++i) {
  14.             st1[i][0] = true;
  15.             dfs(i, 0, st1);
  16.         }
  17.         for (int i = 0; i < m; ++i) {
  18.             st1[0][i] = true;
  19.             dfs(0, i, st1);
  20.         }
  21.         for (int i = 0; i < n; ++i) {
  22.             st2[i][m - 1] = true;
  23.             dfs(i, m - 1, st2);
  24.         }
  25.         for (int i = 0; i < m; ++i) {
  26.             st2[n - 1][i] = true;
  27.             dfs(n - 1, i, st2);
  28.         }
  29.         List<List<Integer>> res = new ArrayList<>();
  30.         for (int i = 0; i < n; ++i) 
  31.             for (int j = 0; j < m; ++j) 
  32.                 if (st1[i][j] && st2[i][j]) {
  33.                     List<Integer> list = new ArrayList<>();
  34.                     list.add(i); list.add(j);
  35.                     res.add(new ArrayList<>(list));
  36.                 }
  37.         return res;
  38.     }
  40.     void dfs(int x, int y, boolean[][] st) {
  41.         for (int i = 0; i < 4; ++i) {
  42.             int a = x + dirs[i], b = y + dirs[i + 1];
  43.             if (a < 0 || a >= n || b < 0 || b >= m) continue;
  44.             if (st[a][b]) continue;
  45.             if (h[a][b] < h[x][y]) continue;
  46.             st[a][b] = true;
  47.             dfs(a, b, st); 
  48.         }   
  49.     }
  50. }