有 NN 种物品和一个容量是 VV 的背包，每种物品都有无限件可用。
第 ii 种物品的体积是 vivi，价值是 wiwi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，VN，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 NN 行，每行两个整数 vi,wivi,wi，用空格隔开，分别表示第 ii 种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

00

输入样例

4 5 1 2 2 4 3 4 4 5

输出样例：

10

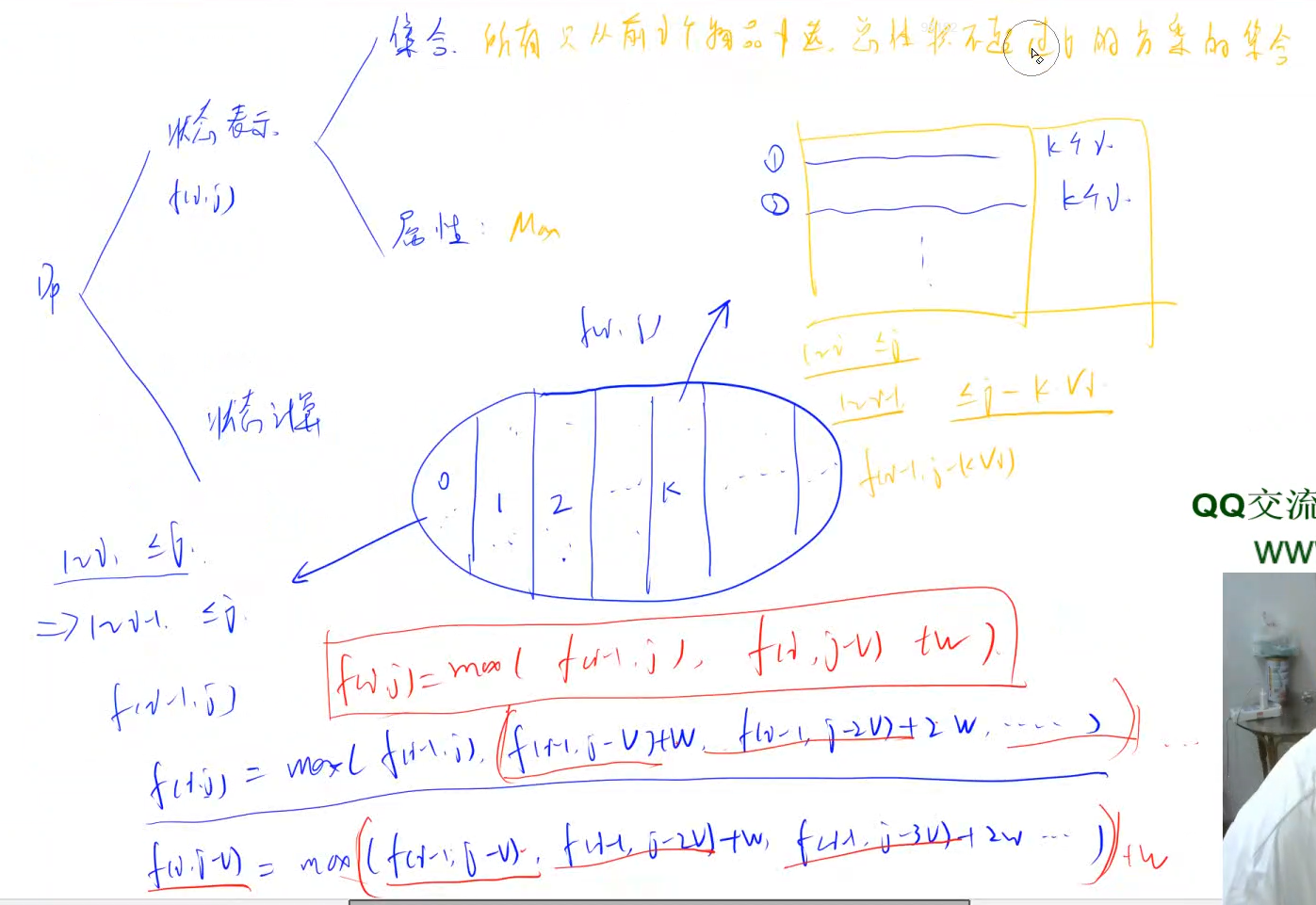
image.png

朴素版本
image.png

  1. #include<iostream>
  3. using namespace std;
  5. const int N = 1010;
  7. int f[N][N];
  8. int n,m;
  9. int v[N],w[N];
  11. //f[i,j] = max(f[i-1,j],f[i,j-v[i]]+w[i])
  12. int main(){
  13.     cin >> n >> m;
  14.     for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
  16.     for(int i = 1; i <= n; ++i)
  17.         for(int j = 0; j <= m; ++j){
  18.             f[i][j] = f[i-1][j];
  19.             if(j >= v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
  20.         }
  21.     cout << f[n][m] << endl;
  22.     return 0;
  23. }

优化版本

  1. #include<iostream>
  3. using namespace std;
  5. const int N = 1010;
  7. int f[N];
  8. int n,m;
  9. int v[N],w[N];
  11. //f[i,j] = max(f[i-1,j],f[i,j-v[i]]+w[i])
  12. int main(){
  13.     cin >> n >> m;
  14.     for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
  16.     for(int i = 1; i <= n; ++i)
  17.         for(int j = v[i]; j <= m; ++j){
  18.             f[j] = max(f[j],f[j-v[i]]+w[i]);
  19.         }
  20.     cout << f[m] << endl;
  21.     return 0;
  22. }