lc2203. 得到要求路径的最小带权子图（dijkstra）

给你一个整数 n ，它表示一个 带权有向 图的节点数，节点编号为 0 到 n - 1 。

同时给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi, weighti] ，表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。

最后，给你三个 互不相同 的整数 src1 ，src2 和 dest ，表示图中三个不同的点。

请你从图中选出一个 边权和最小 的子图，使得从 src1 和 src2 出发，在这个子图中，都 可以 到达 dest 。如果这样的子图不存在，请返回 -1 。

子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。

示例 1：

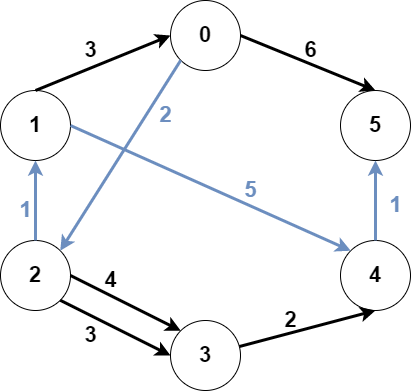
输入：n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
输出：9
解释：
上图为输入的图。
蓝色边为最优子图之一。
注意，子图 [[1,0,3],[0,5,6]] 也能得到最优解，但无法在满足所有限制的前提下，得到更优解。
示例 2：

输入：n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
输出：-1
解释：
上图为输入的图。
可以看到，不存在从节点 1 到节点 2 的路径，所以不存在任何子图满足所有限制。

提示：

3 <= n <= 105
0 <= edges.length <= 105
edges[i].length == 3
0 <= fromi, toi, src1, src2, dest <= n - 1
fromi != toi
src1 ，src2 和 dest 两两不同。
1 <= weight[i] <= 105

class Solution {
    //建立正反图，然后求src1, src2, dest到达的每个点的最短路径，枚举每个点如果能到达三个点，就更新答案
    static int inf = -1;
    public long minimumWeight(int n, int[][] edges, int src1, int src2, int dest) {
        //rh反向图， h正向图
        List<int[]>[] h = create(edges, n, true);
        List<int[]>[] rh = create(edges, n, false);
        //三个点的最短路
        long[] dist1 = dijkstra(src1, n, h);
        long[] dist2 = dijkstra(src2, n, h);
        long[] dist3 = dijkstra(dest, n, rh);
        long res = Long.MAX_VALUE;
        for (int i = 0; i < n; ++i) {
            if (dist1[i] != inf && dist2[i] != inf && dist3[i] != inf)
                res = Math.min(res, dist1[i] + dist2[i] + dist3[i]);
        }
        if (res == Long.MAX_VALUE) return -1;
        return res;
    }
    //建图，邻接矩阵
    private List<int[]>[] create(int[][] edges, int n, boolean sign) {
        List<int[]>[] h = new List[n];
        for (int i = 0; i < n; ++i) 
            h[i] = new ArrayList<int[]>();
        for (int[] t : edges) {
            //正向图
            if (sign) h[t[0]].add(new int[]{t[1], t[2]});
            else h[t[1]].add(new int[]{t[0], t[2]});  
        }
        return h;
    }
    private long[] dijkstra(int start, int n, List<int[]>[] h) {
        long[] dist = new long[n];
        Arrays.fill(dist, inf);
        boolean[] vis = new boolean[n];
        //堆优化
        PriorityQueue<long[]> q = new PriorityQueue<>((a, b) -> Long.compare(a[1], b[1]));
        dist[start] = 0;
        q.add(new long[]{start, 0});
        while (!q.isEmpty()) {
            long[] t = q.poll();
            if (vis[(int)t[0]]) continue;
            vis[(int)t[0]] = true;
            for (int[] next : h[(int)t[0]]) {
                if (dist[next[0]] == inf || dist[next[0]] > t[1] + next[1]) {
                    dist[next[0]] = t[1] + next[1];
                    q.add(new long[]{next[0], dist[next[0]]});
                }
            }
        }
        return dist;
    }
}