lc1289. 下降路径最小和 II（dp & 优化）

给你一个 n x n 整数矩阵 arr ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 arr 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

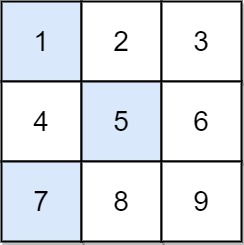
输入：arr = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。
示例 2：

输入：grid = [[7]]
输出：7

提示：

n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99

class Solution {
    /**
    f[i][j] 表示到第i行第j列的最小路径和
    不能枚举正上方的格子
     */
    public int minFallingPathSum(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int[][] f = new int[n + 1][m + 1];
        //初始化第一行
        for (int i = 0; i < m; ++i) f[0][i] = grid[0][i];
        for (int i = 1; i < n; ++i) 
            for (int j = 0; j < m; ++j) {
                f[i][j] = Integer.MAX_VALUE;
                int val = grid[i][j];
                //需要枚举上一行的列数保证不能跟当前列相等
                for (int k = 0; k < m; ++k) 
                    if (k != j) 
                        f[i][j] = Math.min(f[i][j], f[i - 1][k] + val);
            } 
        int res = Integer.MAX_VALUE;
        for (int i = 0; i < m; ++i) 
            res = Math.min(res, f[n - 1][i]);
        return res;
    }
}

优化

class Solution {
    /**
    f[i][j] 表示到第i行第j列的最小路径和
    不能枚举正上方的格子
    优化：由于我们每次都得枚举上一行的每列，所以是n3方
    其实我们只要维护每行的最小值，和次小值即可，当我们访问最小值所对应的j时，换成次小值即可，其他均采用最小值
     */
    public int minFallingPathSum(int[][] grid) {
        int n = grid.length;
        int[][] f = new int[n + 1][n + 1];
        //a 表示最小值下标， b表示次小值下标
        int a = -1, b = -1;
        //初始化第一行
        for (int i = 0; i < n; ++i) {
            f[0][i] = grid[0][i];
            if (a == -1 || grid[0][i] < f[0][a]) {
                b = a;
                a = i;
            } else if (b == -1 || grid[0][i] < f[0][b]) 
                b = i;
        }
        for (int i = 1; i < n; ++i) {
            int i1 = -1, i2 = -1;   //保存当前行的最小值和次小值下标
            for (int j = 0; j < n; ++j) {
                f[i][j] = Integer.MAX_VALUE;
                int val = grid[i][j];
                //判断是不是最小值下标
                if (j != a) f[i][j] = f[i - 1][a] + val;
                else f[i][j] = f[i - 1][b] + val;
                //更新最小值次小值下标
                //注意这里用来更新的是f[i][j]
                if (i1 == -1 || f[i][j] < f[i][i1]) {
                    i2 = i1;
                    i1 = j;
                } else if (i2 == -1 || f[i][j] < f[i][i2]) 
                    i2 = j;
            } 
            a = i1; b = i2;
        }
        int res = Integer.MAX_VALUE;
        for (int i = 0; i < n; ++i) 
            res = Math.min(res, f[n - 1][i]);
        return res;
    }
}