给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。

给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。

示例 1：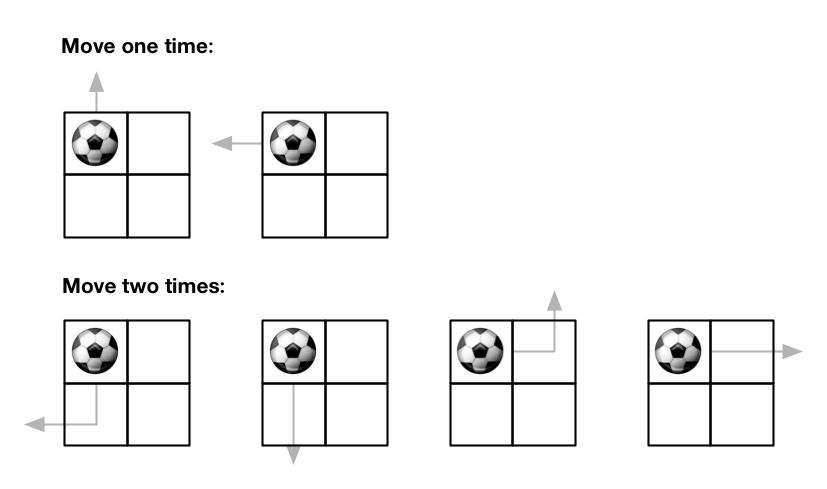
image.png

输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6
示例 2：

输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
输出：12

提示：

1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n

  1. class Solution {
  2.     int mod = (int)1e9 + 7;
  3.     int m, n;
  4.     int[] dx = new int[]{-1, 0, 1, 0}, dy = new int[]{0, 1, 0, -1};
  5.     //暴力dfs会超时，所以需要记忆化搜索
  6.     int[][][] cache;
  7.     public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
  8.         this.m = m; this.n = n;
  9.         cache = new int[m + 1][n + 1][maxMove + 1];
  10.         for (int i = 0; i < m; ++i) 
  11.             for (int j = 0; j < n; ++j) 
  12.                 for (int k = 0; k <= maxMove; ++k) 
  13.                     cache[i][j][k] = -1;
  14.         return dfs(startRow, startColumn, maxMove);
  15.     }
  17.     int dfs(int x, int y, int k) {
  18.         //说明到达了外面
  19.         if (x < 0 || x >= m || y < 0 || y >= n) return 1;
  20.         //没有步数直接返回0
  21.         if (k == 0) return 0;
  22.         //记忆化
  23.         if (cache[x][y][k] != -1) return cache[x][y][k];
  24.         //四个方向扩展
  25.         int sum = 0;
  26.         for (int i = 0; i < 4; ++i) {
  27.             sum += dfs(x + dx[i], y + dy[i], k - 1);
  28.             sum %= mod;
  29.         }
  30.         cache[x][y][k] = sum;
  31.         return sum;
  32.     }
  33. }

dp

  1. class Solution {
  2.     /**
  3.     f[i][j][k] : 当前位置是[i, j],在步数最多是k的情况下移出网格的路径书
  4.     考虑把维度缩小，用idx = i * m + j表示坐标
  5.     状态转移：f[i][j][k] = f[i - 1][j][k - 1] + f[i][j - 1][k - 1] + f[i + 1][j][k - 1] + f[i][j + 1][k -1]
  6.     初始化，把矩阵边缘都初始化为1， 不过需要注意矩阵顶点是有两条路径到外面的
  7.      */
  8.     int m, n, maxMove;
  9.     int mod = (int)1e9 + 7;
  10.     int[] dx = new int[]{-1, 0, 1, 0}, dy = new int[]{0, 1, 0, -1};
  11.     int[][] f;
  12.     public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
  13.         this.m = m; this.n = n; this.maxMove = maxMove;
  14.         f = new int[m * n + 1][maxMove + 1];
  15.         //初始化
  16.         for (int i = 0; i < m; ++i) 
  17.             for (int j = 0; j < n; ++j) 
  18.                 for (int k = 1; k <= maxMove; ++k) {
  19.                     //注意k 是 从1开始， 因为在边缘必须还要移动一格
  20.                     if (i == 0) add(i, j, k);
  21.                     if (i == m - 1) add(i, j, k);
  22.                     if (j == 0) add(i, j, k);
  23.                     if (j == n - 1) add(i, j, k);
  24.                 }
  25.         //dp过程,先从小到大枚举步数，因为我们依赖步数 - 1
  26.         for (int i = 1; i <= maxMove; ++i) 
  27.             for (int idx = 0; idx < m * n; ++idx) {
  28.                 int[] t = parse(idx);
  29.                 int x = t[0], y = t[1];
  30.                 for (int j = 0; j < 4; ++j) {
  31.                     int a = x + dx[j], b = y + dy[j];
  32.                     if (a < 0 || a >= m || b < 0 || b >= n) continue;
  33.                     int nidx = get(a, b);
  34.                     f[idx][i] += f[nidx][i - 1];
  35.                     f[idx][i] %= mod;
  36.                 } 
  37.             }
  38.         return f[get(startRow, startColumn)][maxMove];
  39.     }
  41.     int get(int x, int y) {
  42.         return x * n + y;
  43.     }
  45.     int[] parse(int idx) {
  46.         return new int[]{idx / n, idx % n};
  47.     }
  49.     void add(int i, int j, int k) {
  50.         f[get(i, j)][k] ++;
  51.     }
  52. }