46. 全排列

题目

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

不管是组合还是排列，都是中学中基本的数学问题，代码实现的思路其实也遵循我们大脑思考这类问题的思路。

对于全排列，如果输入，第一个数可以考虑，然后剩下两个位置考虑和，有和两种排列方法。同样第一个位置也可以考虑和。

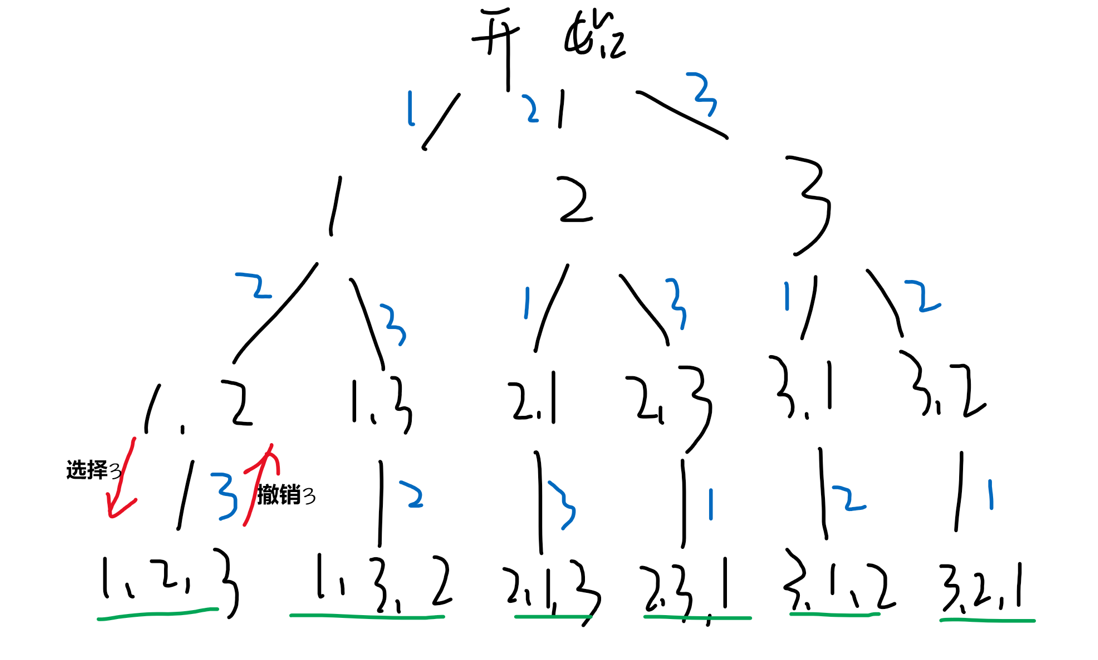
因此，大致的思路就有了，对于输入的个数，我们依次考虑第个位置可以填哪个数，可以按这个思路画出下面的树形图。每个节点做的事情是一样的：在可选择的数中选择一个填充当前位置，然后看下一位置，直到得到一个长度为的排列可能，因此实现起来是递归形式的。

【变量】在实现上，我们如何确定当前位置可以选哪些数呢？可以使用一个和输入数组等长的数组，记录对应下标的数是否用过。每个递归函数内遍历所有的数，遇到用过的数就跳过，没用过的数就可以继续递归。

【回溯过程理解】观察树形图，可以发现决策过程是一个深度优先遍历的过程。红色箭头到是选择的过程，此时因为还没有被选择（当然也只有可以选了）那么我们选择，得到一个排列。此时所有元素都选择过了，无法继续递归，我们开始回溯，到的箭头便是回溯的过程，这个过程中我们要撤销对的选择，回到这里，此时第三个数没有别的选择了，我们再回溯一步，撤销对的选择，回到。正是因为刚撤销了对和的选择，此时我们可以再次选择，之后再选择，第二个排列便产生了。后面过程便类似了。

另外，可以发现，所有的排列可能都在叶子节点（画绿线的），他们的深度是一样的，因此我们可以使用一个变量记录当前的深度，当等于输入数组长度时就表明到了叶子节点。

代码

class Solution {
    List<List<Integer>> ans;
    public List<List<Integer>> permute(int[] nums) {
        ans = new ArrayList<>();
        int n = nums.length;
        boolean[] used = new boolean[n];
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, nums, path, used);
        return ans;
    }
    private void dfs(int n, int[] nums, Deque<Integer> path, boolean[] used) {
        // 递归终止条件，这里省去了depth变量
        if (path.size() == n) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < n; i++) {
            if (used[i]) {
                continue;
            }
            used[i] = true;
            path.offerLast(nums[i]);
            dfs(n, nums, path, used);
            // 回溯，撤销递归前的操作
            used[i] = false;
            path.pollLast();
        }
    }
}