题目

给定一个二叉树的 root ，返回 最长的路径的长度 ，这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。

两个节点之间的路径长度 由它们之间的边数表示。

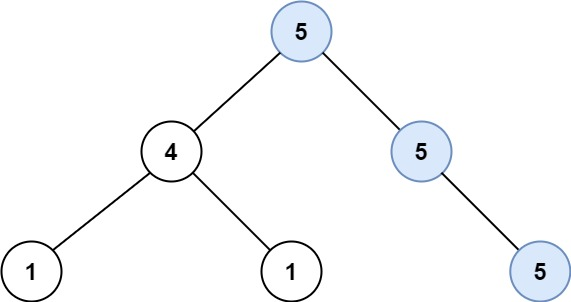
示例 1: image.png

输入：root = [5,4,5,1,1,5]
输出：2

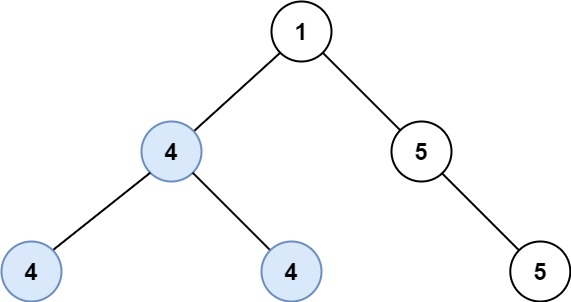
示例 2: image.png

输入：root = [1,4,5,4,4,5]
输出：2

提示:

树的节点数的范围是 [0, 10^4]
-1000 <= Node.val <= 1000
树的深度将不超过 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-univalue-path
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

做过124题之后，这个题就比较好想了，和124思路类似，dfs函数返回root节点左子树或者右子树中较大的路径长度，该路径所有值和root相同。

代码

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class Solution {
  17.     int ans = 0;
  19.     public int longestUnivaluePath(TreeNode root) {
  20.         dfs(root);
  21.         return ans;
  22.     }
  24.     // 返回root节点左子树或者右子树中较大的路径长度，该路径所有值和root相同
  25.     private int dfs(TreeNode root) {
  26.         if (root == null) {
  27.             return 0;
  28.         }
  29.         // 从root节点开始，向左孩子搜索，最长的路径长度
  30.         int left = 0;
  31.         // 左孩子值和root相同，那么两者之间有一条符合条件的边，所以下面+1
  32.         if (root.left != null && root.left.val == root.val) {
  33.             left = dfs(root.left) + 1;
  34.         } else {
  35.             // 左孩子值和root不同，left保持0，但还是要继续搜索左孩子，因为子树可能存在更长的路径
  36.             dfs(root.left);
  37.         }
  38.         int right = 0;
  39.         if (root.right != null && root.right.val == root.val) {
  40.             right = dfs(root.right) + 1;
  41.         } else {
  42.             dfs(root.right);
  43.         }
  44.         // left+right为以root为根节点的子树的最长路径
  45.         ans = Math.max(ans, left + right);
  46.         // 返回左子树或者右子树中较大的路径长度
  47.         return Math.max(left, right);
  48.     }
  49. }

更简洁的写法，出自「这里」，确实很妙。

  1. class Solution {
  2.     int ans = 0;
  4.     public int longestUnivaluePath(TreeNode root) {
  5.         // val初始传递值无关紧要，不影响ans
  6.         dfs(root, 1001);
  7.         return ans;
  8.     }
  10.     // 多了一个val变量，将root值传递到孩子节点，方便判断是否相同
  11.     // 函数返回root子树中单边的和val同值的节点个数，一个节点一条边，因此也是最后要求的边的数目
  12.     private int dfs(TreeNode root, int val) {
  13.         if (root == null) {
  14.             return 0;
  15.         }
  16.         int left = dfs(root.left, root.val);
  17.         int right = dfs(root.right, root.val);
  18.         ans = Math.max(ans, left + right);
  19.         // root节点和其父节点值相同，构成了一条边，这是下面+1的原因；另外再加上单边较长的路径长度，对应代码中max(left, right)
  20.         return root.val == val ? Math.max(left, right) + 1 : 0;
  21.     }
  22. }