440. 字典序的第K小数字

题目

给定整数 n 和 k，返回 [1, n] 中字典序第 k 小的数字。

示例 1:

输入: n = 13, k = 2
输出: 10
解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]，所以第二小的数字是 10。
示例 2:

输入: n = 1, k = 1
输出: 1

提示:

1 <= k <= n <= 10^9

思路

很好的题目，一开始就想到了这其实是一个多叉树的遍历问题，构造出来是一个字典树，如下图所示（画的有点丑…），图中的为，为。前序遍历第个节点就是答案。

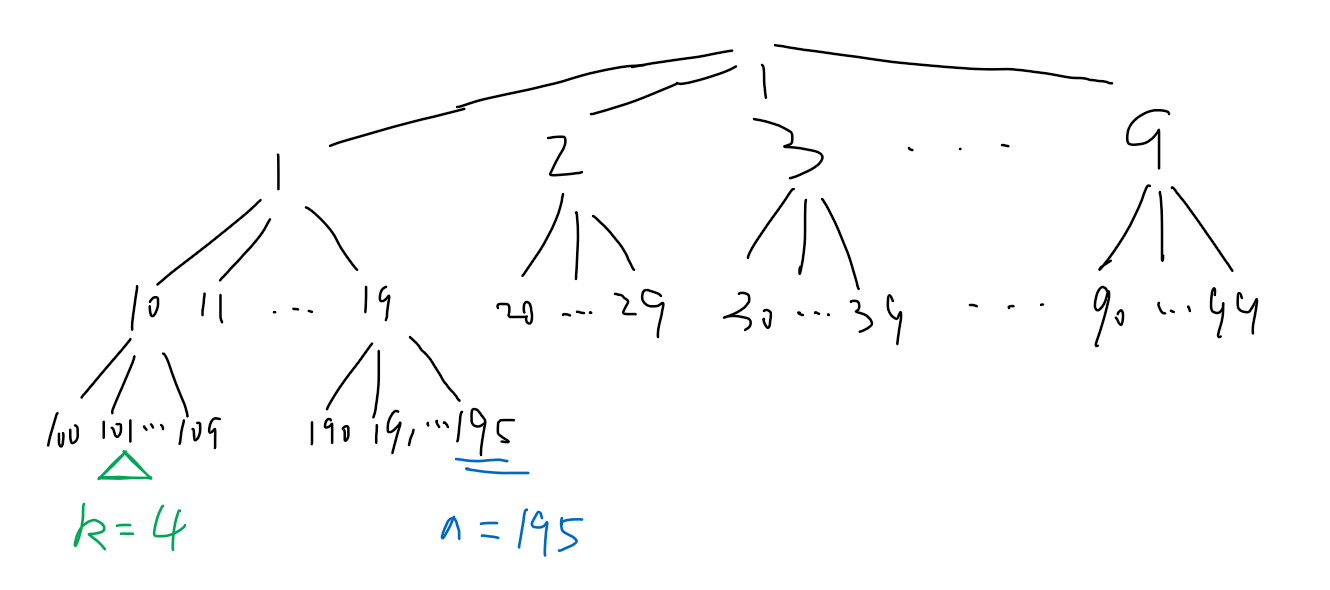
因为的数据范围，所以肯定不能直接挨个节点遍历。

我们可以发现，对于第小的节点，往后再数个就是答案。记以节点为根节点的子树一共有个节点。

如果，那么，第小的数肯定不在这个子树中，直接跳到相邻的节点，反之，在该子树中，更新为左边第一个孩子，即。

通过这个思路，我们可加快寻找第小的数，具体实现见代码。

代码

class Solution {
    public int findKthNumber(int n, int k) {
        // 当前数字，可以看做是一个前序遍历的指针
        int p = 1;
        // 当前数字是第i小的
        int i = 1;
        // 要找第k小的
        while (i < k) {
            int cnt = getChildNum(p, n);
            // 对应思路中的分析
            // 如果cnt <= k - i 第k个肯定不在当前子树中 去p右边相邻的兄弟节点寻找 所以p++
            if (cnt <= k - i) {
                p++;
                i += cnt;
            } else {
                // cnt > k - i 第k个在当前子树中 在当前子树中寻找 先看左边第一个孩子节点 所以p*=10
                p *= 10;
                i++;
            }
        }
        return p;
    }
    // 计算以p为根节点的子树的节点个数（包括p节点）
    private int getChildNum(long p, int n) {
        // 一层一层累加计数的思路计算节点个数
        // 第一层1个 第二层10个 第三层100个
        // cnt为累加的节点个数 最后的返回值
        int cnt = 0;
        // p指向当前层第一个节点 last指向最后一个
        long last = p;
        while (p <= n) {
            // 将当前层个数累加
            cnt += Math.min(last, n) - p + 1;
            // 更新p和last
            p *= 10;
            last = 10 * last + 9;
        }
        return cnt;
    }
}