题目
给你一个二维整数数组 rectangles ,其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ,其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。
第 i 个矩形的 左下角 在 (0, 0) 处,右上角 在 (li, hi) 。
请你返回一个整数数组 count ,长度为 points.length,其中 count[j]是 包含 第 j 个点的矩形数目。
如果 0 <= xj <= li 且 0 <= yj <= hi ,那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ,这个点也被视为被矩形包含。
示例 1:
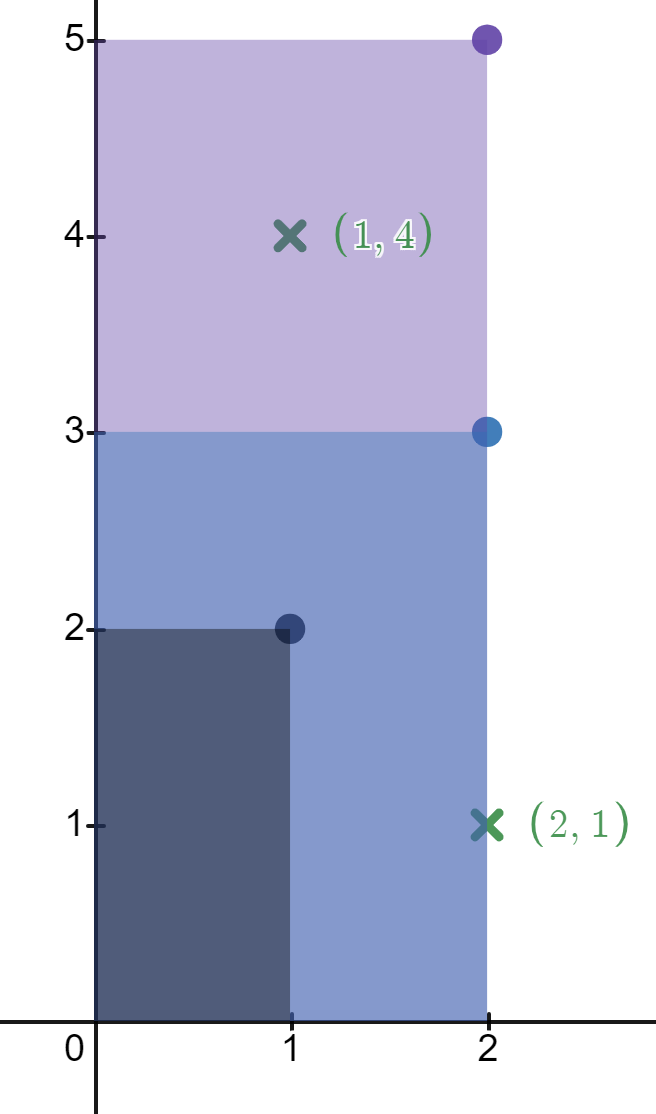
输入:rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
输出:[2,1]
解释:
第一个矩形不包含任何点。
第二个矩形只包含一个点 (2, 1) 。
第三个矩形包含点 (2, 1) 和 (1, 4) 。
包含点 (2, 1) 的矩形数目为 2 。
包含点 (1, 4) 的矩形数目为 1 。
所以,我们返回 [2, 1] 。示例 2:
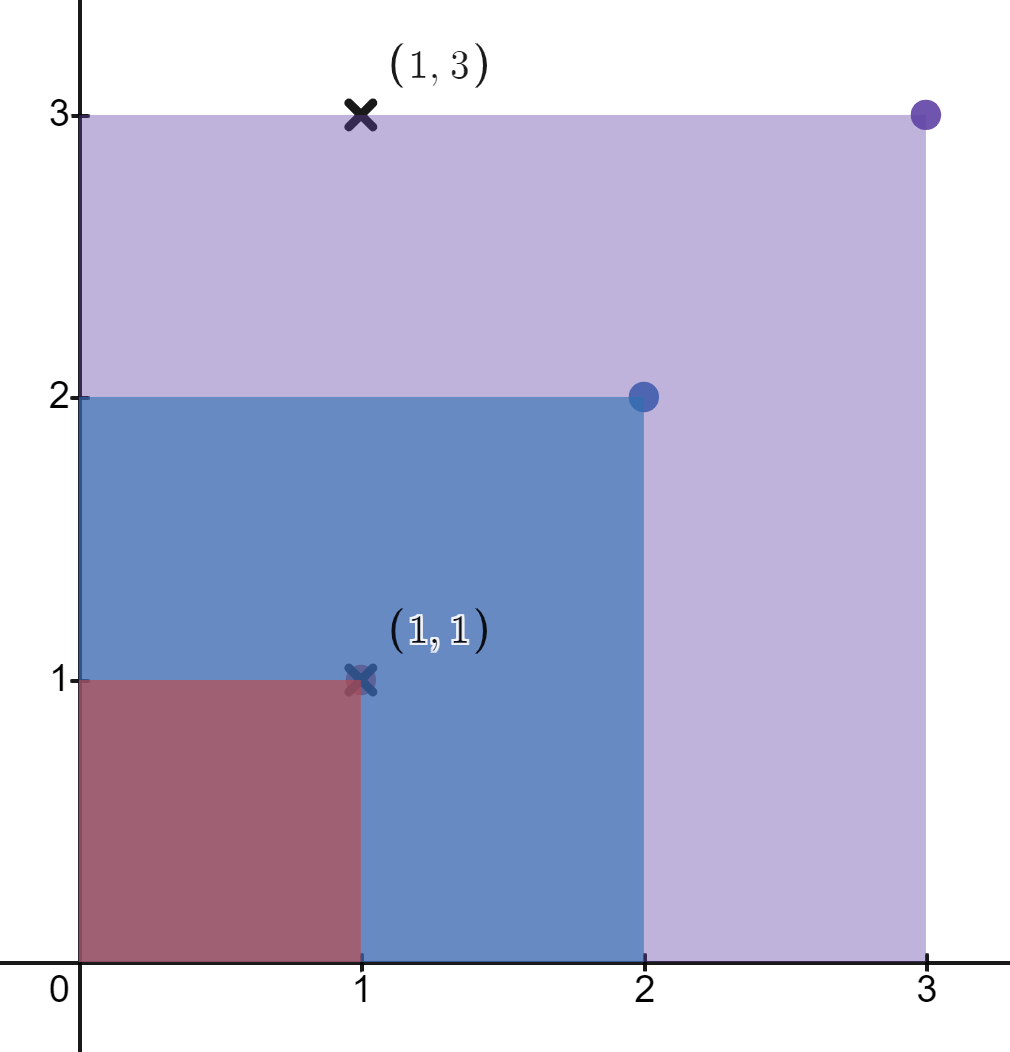
输入:rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
输出:[1,3]
解释:
第一个矩形只包含点 (1, 1) 。
第二个矩形只包含点 (1, 1) 。
第三个矩形包含点 (1, 3) 和 (1, 1) 。
包含点 (1, 3) 的矩形数目为 1 。
包含点 (1, 1) 的矩形数目为 3 。
所以,我们返回 [1, 3] 。提示:
1 <= rectangles.length, points.length <= 5 * 10^4
rectangles[i].length == points[j].length == 2
1 <= li, xj <= 10^9
1 <= hi, yj <= 100
所有 rectangles 互不相同 。
所有 points 互不相同 。来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-number-of-rectangles-containing-each-point
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
比赛结束十分钟做出来了,唉…比赛中总感觉脑子转不动,策略也不太对,第三题做不出来还要去看第四题,第四题果然也做不出来。多练习吧,还是不熟练,足够熟练了就可以像一二题一样很快写出来。
很多没出来的人是因为没注意到x和y范围的差别,但我一开始就注意到了。马上意识到了需要排序加二分,将rectangles按横坐标排序,遍历points,先看横坐标,查找rectangles中第一个不小于当前点的横坐标,但是卡在了不知怎么筛选掉不符合条件的纵坐标,就这样卡了好久,还怀疑是不是思路错了。
其实没错,排序好rectangles后,先预处理出每个 (li, hi) 点右侧的纵坐标不小于k点的数目,其中k属于1到100,每个值都要计算出来。进一步说,使用一个二维数组,大小为n101,n为rectangles长度,arr[i][k]表示按横坐标升序的rectangles中第i个点右侧纵坐标不小于k的点的数目。可以在nk时间内(10^6量级)计算完成,因此该思路可行。见代码一。
代码
代码一 按横坐标排序+预处理
时间复杂度*n%20%2B%20mlogn)#card=math&code=O%28nlogn%20%2B%20max%28h_i%29%2An%20%2B%20mlogn%29&id=M2df6)
空间复杂度*n)#card=math&code=O%28max%28h_i%29%2An%29&id=WTLTa)
其中,
class Solution {public int[] countRectangles(int[][] rectangles, int[][] points) {// rectangles按横坐标升序排列Arrays.sort(rectangles, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);int n = rectangles.length;int m = points.length;// arr[i][k]表示rectangles中第i个点右侧纵坐标不小于k的点的数目int[][] arr = new int[n][101];for (int i = 0; i <= rectangles[n - 1][1]; i++) {arr[n - 1][i]++;}for (int i = n - 2; i >= 0; i--) {for (int j = 0; j < 101; j++) {arr[i][j] = arr[i + 1][j];if (j <= rectangles[i][1]) {arr[i][j]++;}}}int[] ans = new int[m];for (int i = 0; i < m; i++) {int x = points[i][0];int y = points[i][1];// 先查找rectangles中第一个横坐标不小于x的点,返回其下标int k = bsearch(rectangles, x);// k==n说明所有点横坐标都小于x,那么说明point点在所有矩阵外部,答案为0if (k == n) {ans[i] = 0;} else {// 答案第k个点右侧纵坐标不小于y的数目ans[i] = arr[k][y];}}return ans;}public int bsearch(int[][] nums, int target) {int n = nums.length;int low = 0;int high = n;while (low < high) {int mid = low + (high - low) / 2;if (nums[mid][0] < target) {low = mid + 1;} else {high = mid;}}return low;}}
代码二 按纵坐标排序
参考灵茶山艾府的「方法一」。将rectangles和points都按纵坐标降序排列,然后遍历points,将rectangles中纵坐标不小于当前点的横坐标加入一个list,然后对list进行排序,再使用二分查找最小的不小于points横坐标的下标,list中该下标右侧的点就是满足条件的。因为纵坐标最大为100,所以最多排序100次。
时间复杂度nlogn%20%2B%20mlogn)#card=math&code=O%28mlogm%20%2B%20max%28h_i%29nlogn%20%2B%20mlogn%29&id=fabu1),其中,两个数组排序分别需要
和
时间,主体循环内部对list排序最多排序
#card=math&code=max%28h_i%29&id=cDO2Y)次,时间为$ max(h_i)nlogn
mlogn$。
空间复杂度#card=math&code=O%28n%20%2B%20m%29&id=Xm8lv)
class Solution {public int[] countRectangles(int[][] rectangles, int[][] points) {Arrays.sort(rectangles, (a, b) -> b[1] - a[1]);int n = rectangles.length;int m = points.length;// 这里需要声明为包装类型// id数组可以使用流声明: Integer[] id = IntStream.range(0, m).boxed().toArray(Integer[]::new);Integer[] id = new Integer[m];for (int i = 0; i < m; i++) {id[i] = i;}Arrays.sort(id, (a, b) -> points[b][1] - points[a][1]);int[] ans = new int[m];int k = 0;List<Integer> list = new ArrayList<>();for (int i : id) {int start = k;int x = points[i][0];int y = points[i][1];while (k < n && rectangles[k][1] >= y) {list.add(rectangles[k][0]);k++;}// 这里关键,只有list新加入元素才排序,否则会超时if (k > start) {Collections.sort(list);}int j = bsearch(list, x);ans[i] = k - j;}return ans;}public int bsearch(List<Integer> nums, int target) {int n = nums.size();int low = 0;int high = n;while (low < high) {int mid = low + (high - low) / 2;if (nums.get(mid) < target) {low = mid + 1;} else {high = mid;}}return low;}}
代码三 按横坐标排序 不需预处理(推荐)
同样是来自灵山的「方法二」,将rectangles和points都按横坐标降序排列,对比自己的代码一写的真蠢…这里不需要二维数组,只需要一个大小100的一维数组就好了。根本的区别在于这里将rectangles和points都进行了排列,降序遍历points时可以利用前面得到的信息,而代码一不行。
时间复杂度m)#card=math&code=O%28nlogn%20%2B%20mlogm%20%2B%20max%28h_i%29m%29&id=CbUEV)
空间复杂度%20%2B%20m)#card=math&code=O%28max%28h_i%29%20%2B%20m%29&id=ZFcXP)
相比较代码一和二,这个方法时间空间最优,也最为简洁,而且可以使用树状数组优化。
class Solution {public int[] countRectangles(int[][] rectangles, int[][] points) {Arrays.sort(rectangles, (a, b) -> b[0] - a[0]);int n = rectangles.length;int m = points.length;Integer[] id = new Integer[m];for (int i = 0; i < m; i++) {id[i] = i;}Arrays.sort(id, (a, b) -> points[b][0] - points[a][0]);int[] ans = new int[m];int k = 0;// cnt[i]表示当遍历到当前points[j]点时,横坐标不小于points[j][0],且纵坐标为i的点的数目int[] cnt = new int[101];for (int i : id) {int x = points[i][0];int y = points[i][1];while (k < n && rectangles[k][0] >= x) {cnt[rectangles[k][1]]++;k++;}for (int j = y; j < 101; j++) {ans[i] += cnt[j];}}return ans;}}
代码四 树状数组优化代码三
可以使用树状数组对cnt数组的更新和查询进行优化,累加ans[i]的循环就可以省略掉了。
不过这里数据量过小,意义不大,但意识到可以优化是重要的,这里再练习一下树状数组。代码如下:
class Solution {int[] cnt = new int[101];public int[] countRectangles(int[][] rectangles, int[][] points) {Arrays.sort(rectangles, (a, b) -> b[0] - a[0]);int n = rectangles.length;int m = points.length;Integer[] id = new Integer[m];for (int i = 0; i < m; i++) {id[i] = i;}Arrays.sort(id, (a, b) -> points[b][0] - points[a][0]);int[] ans = new int[m];int k = 0;for (int i : id) {int x = points[i][0];int y = points[i][1];while (k < n && rectangles[k][0] >= x) {update(rectangles[k][1], 1);k++;}ans[i] = query(100) - query(y - 1);}return ans;}public void update(int i, int delta) {while (i <= 100) {cnt[i] += delta;i += lowbit(i);}}public int query(int i) {int sum = 0;while (i > 0) {sum += cnt[i];i -= lowbit(i);}return sum;}public static int lowbit(int x) {return x & (-x);}}