310. 最小高度树

题目

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

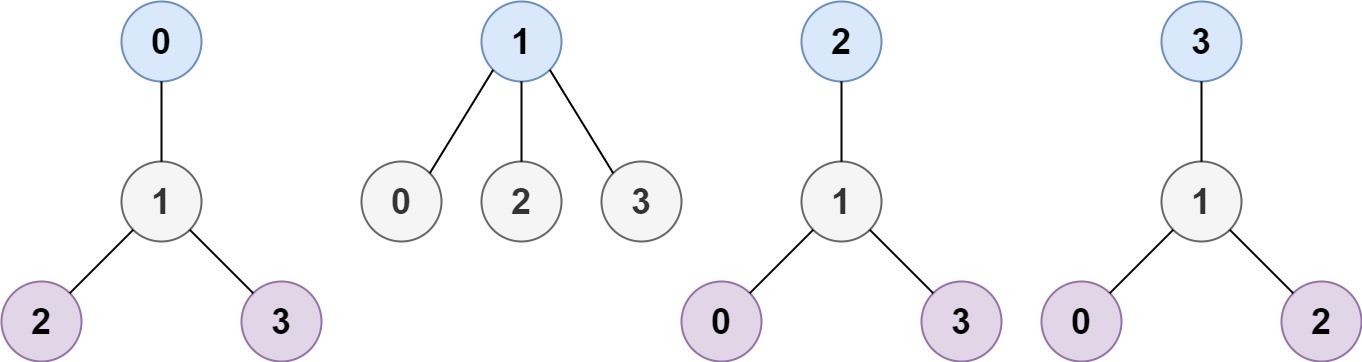
示例 1：

输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
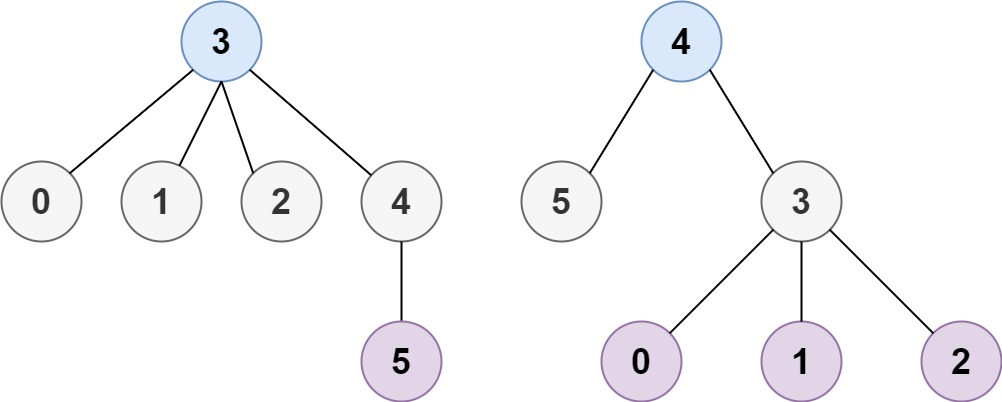
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

提示：

1 <= n <= 2 * 10^4
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入 保证 是一棵树，并且 不会有重复的边

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-height-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

自己想没有思路，一看官解有三种解法，确实挺复杂…好在看了一下并不难懂。

三种方法都基于同一个推论“最小树的根节点一定为树中最长路径的中间节点”。

可以利用或者找到树中的最长路径(第一次接触，需要学习)，然后返回中间节点。分别对应官解的法一法二。

也可以使用拓扑排序，不断消除最长路径两端的节点(度为1)，很有趣的方法。当剩余节点数不大于时就是要找的根节点。

代码基本框架就是拓扑排序 Kahn 算法的框架，需要注意的地方写在注释里了。

代码

拓扑排序

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> ans = new ArrayList<>();
        // 特判，只有一个节点，没有边，但是也要返回这个唯一的节点
        if (n == 1) {
            ans.add(0);
            return ans;
        }
        List<Integer>[] adj = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<>();
        }
        int[] degree = new int[n];
        for (int[] e : edges) {
            adj[e[0]].add(e[1]);
            adj[e[1]].add(e[0]);
            degree[e[0]]++;
            degree[e[1]]++;
        }
        Queue<Integer> queue = new ArrayDeque<>();
        for (int i = 0; i < n; i++) {
            if (degree[i] == 1) {
                queue.offer(i);
            }
        }
        // 不断排除度为1的节点，最后剩下最多两个时停止
        // 注意这里不能用queue.size()>2作为循环条件，有可能刚开始队列中就不多于两个，无法进入循环，从而获得错误答案
        int remain = n;
        while (remain > 2) {
            int size = queue.size();
            remain -= size;
            for (int i = 0; i < size; i++) {
                int cur = queue.poll();
                for (int v : adj[cur]) {
                    degree[v]--;
                    if (degree[v] == 1) {
                        queue.offer(v);
                    }
                }
            }
        }
        // 最后队列中的节点就是要找的根节点，最多两个
        while (!queue.isEmpty()) {
            ans.add(queue.poll());
        }
        return ans;
    }
}