47. 全排列 II

题目

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这个题和题不同的是输入数组可以包含重复数组，如果仍按题解法，输出会有重复的排列，因此需要想办法去掉。

例如输入数组为，我们用和来区分两个相同的，树形图如下。划红线的是重复的排列，我们需要将其去掉，对应应该在红叉处剪枝。

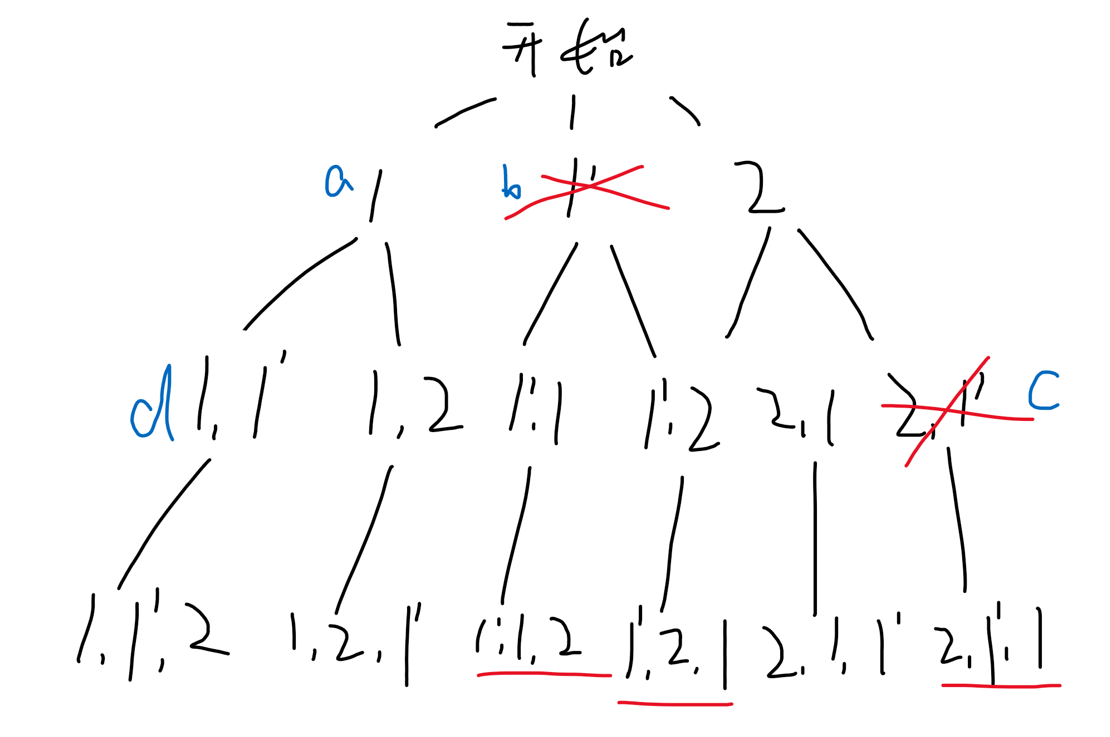
重点就是如何剪枝呢？第一步容易想到的就是我们先对输入数组进行排序，将相同的元素放在一起，这样好判断。另外，我们可以分析，在处为什么会产生和处相同的分支呢？这是因为排序后的和前面的在数值上相等，尽管最后和的位置不同，但两者数值相同，表示的排列也相同，因此产生了重复。

进一步，我们发现，正是因为前面的在处可以被选择，才会在下一层选择后造成重复。同样，处也是因为前面的被撤销过进而可以选择，所以再次选择时会重复。而处则不同，此处已经被选择，那么便不会产生重复。

综上，我们去重的条件就是当前选择的数等于排序后数组前一个数，并且前一个数未被选择。

代码

class Solution {
    List<List<Integer>> ans;
    public List<List<Integer>> permuteUnique(int[] nums) {
        // 对输入数组排序，方便去重剪枝
        Arrays.sort(nums);
        ans = new ArrayList<>();
        int n = nums.length;
        boolean[] used = new boolean[n];
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, nums, path, used);
        return ans;
    }
    private void dfs(int n, int[] nums, Deque<Integer> path, boolean[] used) {
        if (path.size() == n) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < n; i++) {
            // 和46题不同的是，这里添加了一种跳过的情况：nums[i] == nums[i - 1] && !used[i - 1] 即当前数等于前一个数，并且前一个数未被选择
            if (used[i] || i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }
            used[i] = true;
            path.offerLast(nums[i]);
            dfs(n, nums, path, used);
            used[i] = false;
            path.pollLast();
        }
    }
}