498. 对角线遍历

题目

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

示例 1：

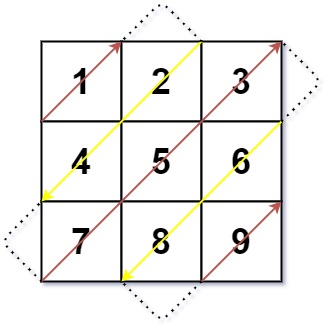
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]

示例 2：

输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 10^4
1 <= m * n <= 10^4
-10^5 <= mat[i] [j] <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/diagonal-traverse
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

顺着遍历的思路进行模拟，使用一个变量记录当前遍历方向，如1表示从下向上遍历（行数-1，列数+1），-1表示从上向下遍历（行数+1，列数-1）。

一开始从(0,0)开始遍历，方向为从下向上，每遍历完一个数就进行「行数-1，列数+1」的操作，直至出界，然后变换方向，同时计算下一次遍历的起点。

对于方向从1变为-1，在矩阵上半部分，方向-1的起点为方向1的起点的「右边」的点；在矩阵下半部分，方向-1的起点为方向1的起点的「下边」的点。

对于方向从-1变为1，在矩阵上半部分，方向1的起点为方向-1的起点的「下边」的点；在矩阵下半部分，方向1的起点为方向-1的起点的「右边」的点。

「官解」的思路更好一点，根据横纵坐标之和的奇偶性来判断方向。

代码

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        int r = 0;
        int c = 0;
        int[] ans = new int[m * n];
        int k = 0;
        int dir = 1;
        while (k < m * n) {
            if (dir == 1) {
                while (r >= 0 && c < n) {
                    ans[k++] = mat[r--][c++];
                }
                // 循环结束，r和c出界了，要各自退一步拉回来
                r++;
                c--;
                // 在矩阵上半部分，下一次的起点为当前点「右边」的点
                if (c + 1 < n) {
                    c++;
                } else {
                    // 在矩阵下半部分，下一次的起点为当前点「下边」的点
                    r++;
                }
            } else {
                while (r < m && c >= 0) {
                    ans[k++] = mat[r++][c--];
                }
                r--;
                c++;
                if (r + 1 < m) {
                    r++;
                } else {
                    c++;
                }
            }
            dir *= -1;
        }
        return ans;
    }
}