2055. 蜡烛之间的盘子

题目

给你一个长桌子，桌子上盘子和蜡烛排成一列。给你一个下标从 0 开始的字符串 s ，它只包含字符 ‘‘ 和 ‘|’ ，其中 ‘‘ 表示一个 盘子 ，’|’ 表示一支 蜡烛 。

同时给你一个下标从 0 开始的二维整数数组 queries ，其中 queries[i] = [lefti, righti] 表示 子字符串 s[lefti…righti] （包含左右端点的字符）。对于每个查询，你需要找到 子字符串中 在 两支蜡烛之间 的盘子的 数目 。如果一个盘子在 子字符串中 左边和右边 都 至少有一支蜡烛，那么这个盘子满足在 两支蜡烛之间 。

比方说，s = “|||||“ ，查询 [3, 8] ，表示的是子字符串 “||**|” 。子字符串中在两支蜡烛之间的盘子数目为 2 ，子字符串中右边两个盘子在它们左边和右边 都 至少有一支蜡烛。
请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1:

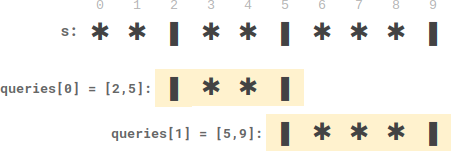
输入：s = “||*|”, queries = [[2,5],[5,9]]
输出：[2,3]
解释：

• queries[0] 有两个盘子在蜡烛之间。
• queries[1] 有三个盘子在蜡烛之间。

示例 2:

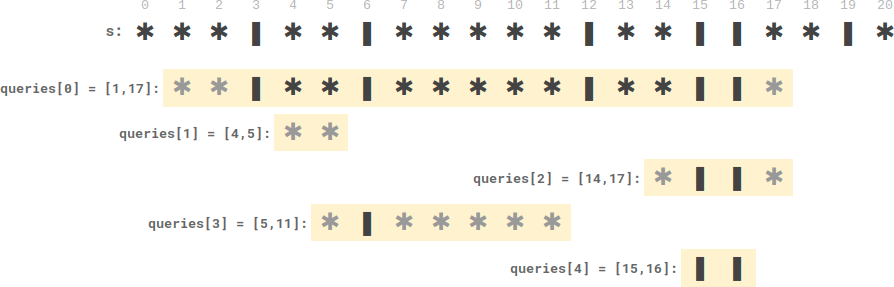
输入：s = “||||||*”, queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
输出：[9,0,0,0,0]
解释：

• queries[0] 有 9 个盘子在蜡烛之间。
• 另一个查询没有盘子在蜡烛之间。

提示：

3 <= s.length <= 10^5
s 只包含字符 ‘*’ 和 ‘|’ 。
1 <= queries.length <= 10^5
queries[i].length == 2
0 <= lefti <= righti < s.length

思路

首先看数据范围，那最多)#card=math&code=O%28nlog%28n%29%29&id=rNz2r)，或者#card=math&code=O%28n%29&id=Ak6bp)了。

对于每个查询区间，我们需要先找到最左边和最右边的蜡烛，记作和，然后统计中间的盘子数目。

具体地，对于一个查询区间，我们需要寻找到右边的第一个蜡烛，以及左边的第一个蜡烛。那么我们需要预处理出每个位置左边和右边的第一个蜡烛位置，可以在线性时间内解决。或者不预处理，使用二分也可以。

统计一个区间内盘子数目就简单了，区间和使用前缀和数组可以解决。

一些解释和细节写在注释里了。

代码

class Solution {
    public int[] platesBetweenCandles(String s, int[][] queries) {
        int n = queries.length;
        int m = s.length();
        int[] ans = new int[n];
        // leftCan[i]表示i左边左边第一个蜡烛的位置，rightCan同理
        int[] leftCan = new int[m];
        int[] rightCan = new int[m];
        // 前缀数组，用于求区间内盘子数目
        int[] prePlate = new int[m];
        // 初始化为-1 分别表示左边右边没有蜡烛
        Arrays.fill(leftCan, -1);
        Arrays.fill(rightCan, -1);
        // 三个边界处理
        if (s.charAt(0) == '|') {
            leftCan[0] = 0;
        } else {
            prePlate[0] = 1;
        }
        if (s.charAt(m - 1) == '|') {
            rightCan[m - 1] = m - 1;
        }
        for (int i = 1; i < m; i++) {
            leftCan[i] = s.charAt(i) == '|' ? i : leftCan[i - 1];
            rightCan[m - i - 1] = s.charAt(m - i - 1) == '|' ? m - i - 1 : rightCan[m - i];
            prePlate[i] = prePlate[i - 1] + (s.charAt(i) == '*' ? 1 : 0);
        }
        for (int i = 0; i < n; i++) {
            // l和r分别为查询区间内最左边和最右边的蜡烛
            int l = rightCan[queries[i][0]];
            int r = leftCan[queries[i][1]];
            // 注意 l和r不能是-1
            if (l >= 0 && r >= 0 && l + 1 < r) {
                ans[i] = prePlate[r] - prePlate[l];
            }
        }
        return ans;
    }
}